
1.(1994年全国高考)已知z=1+i,
(Ⅰ)设ω=z2+3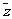 -4,求ω的三角形式;;
-4,求ω的三角形式;;
(Ⅱ)如果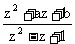 =1-i,求实数a,b的值.
=1-i,求实数a,b的值.
3.
(2001年全国高考)已知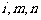 是正整数,且
是正整数,且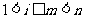 .
.
(Ⅰ)证明 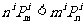 ;
;
(Ⅱ)证明 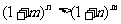 .
.
[答案与提示:1.放缩法,利用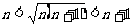 ; 2.略; 3.利用排列数公式及二项式定理.]
; 2.略; 3.利用排列数公式及二项式定理.]
2. (1993年全国高考)如果关于x的实系数二次方程x2+ax+b=0有两个实数根α、β,证明:
Ⅰ.如果|α|<2,|β|<2,那么2|a|<4+b且|b|<4;
Ⅱ.如果2|a|<4+b且|b|<4,那么|α|<2,|β|<2.(93年(29)10分)
1.
(1985年全国高考)设a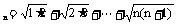 (n=1,2,3……),
(n=1,2,3……),
证明不等式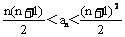 对所有的正整数n都成立.
对所有的正整数n都成立.
2.
(2000年全国高考)设函数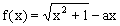 ,其中a>0.
,其中a>0.
(I)解不等式f(x)≤1;
(II)求a的取值范围,使函数f(x)在区间[0,+∞]上是单调函数.
[答案与提示:1.当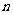 为奇数时,不等式的解集为
为奇数时,不等式的解集为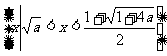 ;当
;当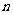 为偶数时,解集为
为偶数时,解集为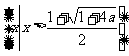 . 2.(I)0<a<1时,所给不等式的解集为
. 2.(I)0<a<1时,所给不等式的解集为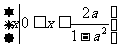 ,当a≥1时,所给不等式的解集为{x|x≥0};(II)当且仅当a≥1时,函数f(x )在区间[0,+∞]上是单调函数.]
,当a≥1时,所给不等式的解集为{x|x≥0};(II)当且仅当a≥1时,函数f(x )在区间[0,+∞]上是单调函数.]
1.
(1991年全国高考)已知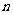 为自然数,实数
为自然数,实数 ,解关于x的不等式:
,解关于x的不等式:
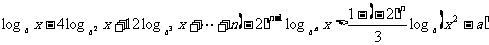 .
.
2.
(1999年全国高考)已知函数 的图象是自原点出发的一条折线,当n≤y≤n+1(n=0,1,2,…)时,该图象是斜率为
的图象是自原点出发的一条折线,当n≤y≤n+1(n=0,1,2,…)时,该图象是斜率为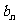 的线段(其中正常数
的线段(其中正常数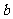 ≠1),设数列
≠1),设数列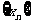 由
由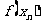 =
=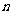 (
(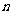 =1,2,…)定义
=1,2,…)定义
(Ⅰ)求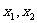 和
和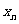 的表达式;
的表达式;
(Ⅱ)求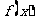 的表达式,并写出其定义域;
的表达式,并写出其定义域;
(Ⅲ)证明 的图象与
的图象与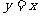 的图象没有横坐标大于1的交点.
的图象没有横坐标大于1的交点.
[答案与提示:1.不存在满足题意的常数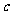 . 2.(Ⅰ)
. 2.(Ⅰ)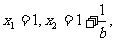
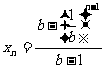 ;(Ⅱ)当
;(Ⅱ)当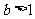 时,
时,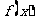 的定义域为
的定义域为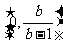 ,当
,当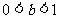 时,
时,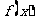 的定义域为
的定义域为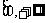 ;(Ⅲ)略.]
;(Ⅲ)略.]
1.
(1995年全国高考)设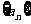 是由正数组成的等比数列,
是由正数组成的等比数列,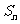 是其前n项和,
是其前n项和,
(Ⅰ)证明: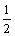 (
(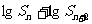 )<
)<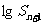 ;
;
(Ⅱ)是否存在常数c>0,使得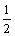 [lg(
[lg(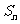 -c)+lg(
-c)+lg(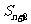 -c)]<lg(
-c)]<lg(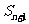 -c)成立?并证明你的结论.
-c)成立?并证明你的结论.
2.
(2002年全国高考)设数列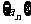 满足:
满足: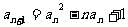
(1)
当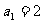 时,求
时,求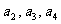 ,并由此猜想出
,并由此猜想出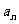 的一个通项公式;
的一个通项公式;
(2)
当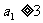 时,证明对所有的
时,证明对所有的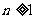 ,有
,有
(I)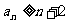 ;
;
(ii)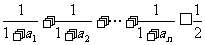 .
.
[答案与提示:1.(1) . (2)当
. (2)当 时,
时,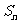 >
>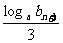 ;当
;当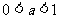 时,
时,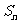 <
<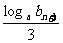 . 2.(1)
. 2.(1)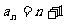 ,(2)略.]
,(2)略.]
1.
(1998年全国高考)已知数列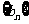 是等差数列,
是等差数列,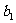 =1,
=1,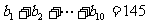 .
①求数列
.
①求数列 的通项
的通项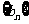 ;
②设数列
;
②设数列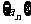 的通项
的通项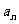 =
=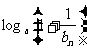 (其中
(其中 且
且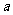 ≠1),记
≠1),记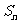 是数列
是数列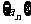 的前n项和.试比较
的前n项和.试比较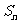 与
与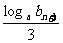 的大小,并证明你的结论.
的大小,并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com