
36.(2009辽宁卷理)以知F是双曲线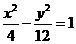 的左焦点,
的左焦点,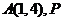 是双曲线右支上的动点,则
是双曲线右支上的动点,则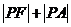 的最小值为
。
的最小值为
。
[解析]注意到P点在双曲线的两只之间,且双曲线右焦点为F’(4,0),
于是由双曲线性质|PF|-|PF’|=2a=4
而|PA|+|PF’|≥|AF’|=5
两式相加得|PF|+|PA|≥9,当且仅当A、P、F’三点共线时等号成立.
[答案]9
35.(2009福建卷理)过抛物线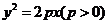 的焦点F作倾斜角为
的焦点F作倾斜角为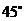 的直线交抛物线于A、B两点,若线段AB的长为8,则
的直线交抛物线于A、B两点,若线段AB的长为8,则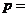 ________________
________________ 

[解析]由题意可知过焦点的直线方程为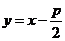 ,联立有
,联立有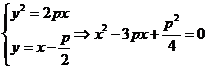 ,又
,又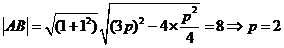 。
。
[答案] 2
34.(2009湖南卷文)过双曲线C: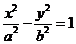
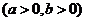 的一个焦点作圆
的一个焦点作圆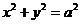 的两条切线,切点分别为A,B,若
的两条切线,切点分别为A,B,若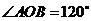 (O是坐标原点),则双曲线线C的离心率为 .
(O是坐标原点),则双曲线线C的离心率为 .
[解析]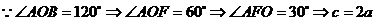 ,
, 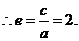
[答案]2
33.(2009四川卷文)抛物线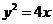 的焦点到准线的距离是
.
的焦点到准线的距离是
.
[解析]焦点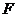 (1,0),准线方程
(1,0),准线方程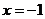 ,∴焦点到准线的距离是2.
,∴焦点到准线的距离是2.
[答案]2
32.(2009广东卷理)巳知椭圆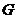 的中心在坐标原点,长轴在
的中心在坐标原点,长轴在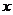 轴上,离心率为
轴上,离心率为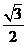 ,且
,且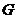 上一点到
上一点到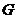 的两个焦点的距离之和为12,则椭圆
的两个焦点的距离之和为12,则椭圆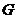 的方程为 .
的方程为 .
[解析]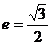 ,
,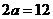 ,
,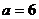 ,
,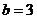 ,则所求椭圆方程为
,则所求椭圆方程为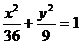 .
.
[答案]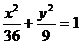
31.(2009北京文、理)椭圆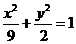 的焦点为
的焦点为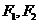 ,点P在椭圆上,若
,点P在椭圆上,若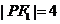 ,则
,则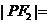 ;
;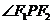 的大小为 .
的大小为 .
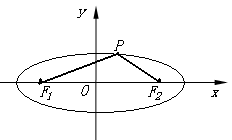 .w[解析]本题主要考查椭圆的定义、焦点、长轴、短轴、焦距之间的关系以及余弦定理. 属于基础知识、基本运算的考查.
.w[解析]本题主要考查椭圆的定义、焦点、长轴、短轴、焦距之间的关系以及余弦定理. 属于基础知识、基本运算的考查.
∵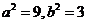 ,
,
∴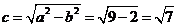 ,
,
∴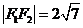 ,
,
又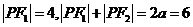 ,∴
,∴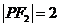 ,
,
又由余弦定理,得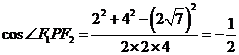 ,
,
∴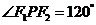 ,故应填
,故应填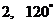 .
.
30.(2009重庆卷文、理)已知椭圆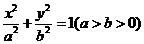 的左、右焦点分别为
的左、右焦点分别为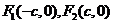 ,若椭圆上存在一点
,若椭圆上存在一点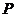 使
使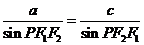 ,则该椭圆的离心率的取值范围为
.
,则该椭圆的离心率的取值范围为
.
[解析1]因为在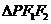 中,由正弦定理得
中,由正弦定理得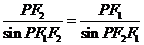
则由已知,得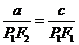 ,即
,即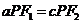
设点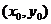 由焦点半径公式,得
由焦点半径公式,得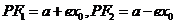 则
则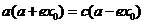
记得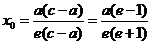 由椭圆的几何性质知
由椭圆的几何性质知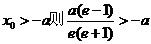 ,整理得
,整理得
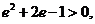 解得
解得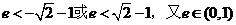 ,故椭圆的离心率
,故椭圆的离心率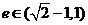
[解析2] 由解析1知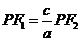 由椭圆的定义知
由椭圆的定义知 

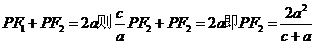 ,由椭圆的几何性质知
,由椭圆的几何性质知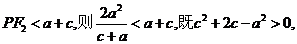 所以
所以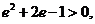 以下同解析1.
以下同解析1.
[答案]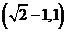
29.(2009宁夏海南卷理)设已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交于A,B两点。若AB的中点为(2,2),则直线l的方程为_____________.
[解析]抛物线的方程为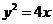 ,
,
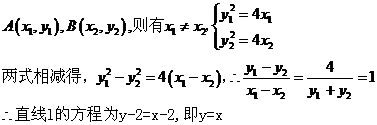
[答案]y=x
28.(2009四川卷理)已知直线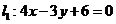 和直线
和直线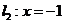 ,抛物线
,抛物线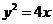 上一动点
上一动点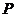 到直线
到直线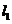 和直线
和直线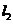 的距离之和的最小值是( )
的距离之和的最小值是( )
A.2
B.3 C.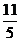 D.
D.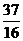
[考点定位]本小题考查抛物线的定义、点到直线的距离,综合题。
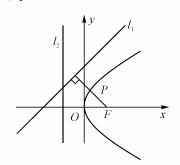 [解析1]直线
[解析1]直线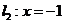 为抛物线
为抛物线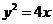 的准线,由抛物线的定义知,P到
的准线,由抛物线的定义知,P到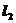 的距离等于P到抛物线的焦点
的距离等于P到抛物线的焦点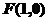 的距离,故本题化为在抛物线
的距离,故本题化为在抛物线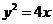 上找一个点
上找一个点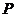 使得
使得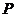 到点
到点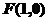 和直线
和直线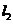 的距离之和最小,最小值为
的距离之和最小,最小值为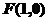 到直线
到直线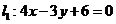 的距离,即
的距离,即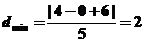 ,故选择A。
,故选择A。
[解析2]如图,由题意可知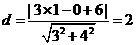
[答案]A
27.(2009天津卷理)设抛物线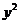 =2x的焦点为F,过点M(
=2x的焦点为F,过点M(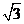 ,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,
,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,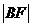 =2,则
=2,则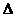 BCF与
BCF与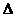 ACF的面积之比
ACF的面积之比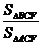 =( )
=( )
A.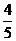 B.
B.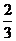 C.
C.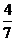 D.
D.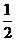
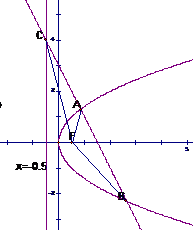
[解析]由题知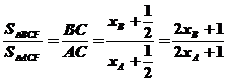 ,
,
又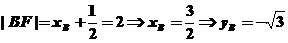
由A、B、M三点共线有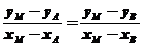 即
即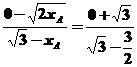 ,故
,故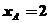 ,
, 
∴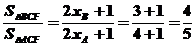 ,故选择A。
,故选择A。
[答案]A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com