
20.(本题满分16分)
设函数 的定义域为
的定义域为 ,值域为
,值域为 ,如果存在函数
,如果存在函数 ,使得函数
,使得函数 的值域仍然是
的值域仍然是 ,那么,称函数
,那么,称函数 是函数
是函数 的一个等值域变换,
的一个等值域变换,
(1)判断下列 是不是
是不是 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由;

 ,
, ;
;

 ,
, ;
;
(2)设 的值域
的值域 ,已知
,已知 是
是 的一个等值域变换,且函数
的一个等值域变换,且函数 的定义域为
的定义域为 ,求实数
,求实数 的值;
的值;
(3)设函数 的定义域为
的定义域为 ,值域为
,值域为 ,函数
,函数 的定义域为
的定义域为 ,值域为
,值域为 ,写出
,写出 是
是 的一个等值域变换的充分非必要条件(不必证明),并举例说明条件的不必要性.
的一个等值域变换的充分非必要条件(不必证明),并举例说明条件的不必要性.
解:(1) :函数
:函数 的值域为
的值域为 ,
, ,
, ,
,
所以, 不是
不是 的一个等值域变换; …………2分
的一个等值域变换; …………2分
 :
: ,即
,即 的值域为
的值域为 ,
,
当 时,
时, ,即
,即 的值域仍为
的值域仍为 ,
,
所以, 是
是 的一个等值域变换;
…………5分
的一个等值域变换;
…………5分
(2) 的值域为
的值域为 ,由
,由 知
知 ,
,
即 定义域为
定义域为 ,
…………6分
,
…………6分
因为 是
是 的一个等值域变换,且函数
的一个等值域变换,且函数 的定义域为
的定义域为 ,
,
所以, 的值域为
的值域为 ,
…………8分
,
…………8分
 ,
,
所以,
恒有 ,且存在
,且存在 使两个等号分别成立,………10分
使两个等号分别成立,………10分
于是 ,
,
解得  或
或 …………13分
…………13分
(3)设函数 的定义域为
的定义域为 ,值域为
,值域为 ,函数
,函数 的定义域为
的定义域为 ,值域为
,值域为 ,则
,则 是
是 的一个等值域变换的充分非必要条件是“
的一个等值域变换的充分非必要条件是“ =
= ”. …………15分
”. …………15分
条件的不必要性的一个例子是.
 ,
,
 ,
,
 ,
, ,
,
此时 ,但
,但 的值域仍为
的值域仍为 ,
,
即
 是
是
 的一个等值域变换。…………18分
的一个等值域变换。…………18分
(反例不唯一)
教研室内部备用题选编
19.(1)由已知 ,
,
 ,得
,得



由数列 是等差数列,得
是等差数列,得


所以,
 ,
, ,得
,得 .…………………5分
.…………………5分
(2)由 ,可得
,可得


且当 时,
时,

所以,当 时,
时,

 ,…………………4分
,…………………4分
因此,数列 是一个公比为
是一个公比为 的等比数列.…………………………………………1分
的等比数列.…………………………………………1分
(3)解答一:写出必要条件,如,由(1)知,当 时,数列
时,数列 是等差数列,
是等差数列,
所以 是数列
是数列 为等比数列的必要条件. ………………………………3分
为等比数列的必要条件. ………………………………3分
解答二:写出充分条件,如 或
或 等,并证明 ……………… 5分
等,并证明 ……………… 5分
解答三: 是等比数列的充要条件是
是等比数列的充要条件是
 ……………………2分
……………………2分
充分性证明:
若
 ,则由已知
,则由已知 ,
,
 得
得


所以, 是等比数列.……………………………………………………………2分
是等比数列.……………………………………………………………2分
必要性证明:若 是等比数列,由(2)知,
是等比数列,由(2)知,


 ,
,
 . …………………………………………1分
. …………………………………………1分
当 时,
时,
 .
.
上式对 也成立,所以,数列
也成立,所以,数列 的通项公式为:
的通项公式为:

 .
.
所以,当 时,数列
时,数列 是以
是以 为首项,
为首项, 为公差的等差数列.
为公差的等差数列.
所以, .……………………………………………………………………1分
.……………………………………………………………………1分
当 时,
时,
 .
.
上式对 也成立,所以,
也成立,所以,

 ……………………1分
……………………1分
所以,
 . …………………………………………1分
. …………………………………………1分
即,等式 对于任意实数
对于任意实数 均成立.
均成立.
所以,
 .……………………………………………………………1分
.……………………………………………………………1分
19.(本题满分16分).
已知定义在 上的函数
上的函数 和数列
和数列 满足下列条件:
满足下列条件:
 ,
, ,当
,当 且
且 时,
时, 且
且 .
.
其中 、
、 均为非零常数.
均为非零常数.
(1)若数列 是等差数列,求
是等差数列,求 的值;
的值;
(2)令
 ,若
,若 ,求数列
,求数列 的通项公式;
的通项公式;
(3)试研究数列 为等比数列的条件,并证明你的结论.
为等比数列的条件,并证明你的结论.
说明:对于第3小题,将根据写出的条件所体现的对问题探究的完整性,给予不同的评分。
18.(本题满分16分)本大题共有2个小题,第1小题满分8分,第2小题满8分.
2010年上海世博会组委会为保证游客参观的顺利进行,对每天在各时间段进入园区和离开园区的人数作了一个模拟预测. 为了方便起见,以10分钟为一个计算单位,上午9点10分作为第一个计算人数的时间,即 ;9点20分作为第二个计算人数的时间,即
;9点20分作为第二个计算人数的时间,即
 ;依此类推
;依此类推 ,把一天内从上午9点到晚上24点分成了90个计算单位.
,把一天内从上午9点到晚上24点分成了90个计算单位.
对第 个时刻进入园区的人数
个时刻进入园区的人数 和时间
和时间 (
( )满足以下关系(如图1):
)满足以下关系(如图1):

 ,
,
|
|
 个时刻离开园区的人数
个时刻离开园区的人数 和时间
和时间
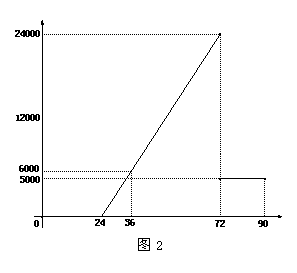
 (
( )满足以下关系(如图2):
)满足以下关系(如图2):

(1)试计算在当天下午3点整(即15点整)
时,世博园区内共有多少游客?
(2)请求出当天世博园区内游客总人数最多
的时刻.
解:(1)当 且
且 时,
时, ,
,
当 且
且 时,
时, ……………………………………………2分
……………………………………………2分
所以 …
…

 ×
×

 ×
×





 ;……………………………………………………2分
;……………………………………………………2分
另一方面,已经离开的游客总人数是:

 ×
×

 ;……………2分
;……………2分
所以 (人)
(人)
故当天下午3点整(即15点整)时,世博园区内共有 位游客. …………2分
位游客. …………2分
(2)当 时园内游客人数递增;当
时园内游客人数递增;当 时园内游客人数递减.
时园内游客人数递减.
(i)当 时,园区人数越来越多,人数不是最多的时间;……………………2分
时,园区人数越来越多,人数不是最多的时间;……………………2分
(ii)当 时,令
时,令 ,得出
,得出 ,
,
即当 时,进入园区人数多于离开人数,总人数越来越多;……………2分
时,进入园区人数多于离开人数,总人数越来越多;……………2分
当 时,
时, ,进入园区人数多于离开人数,总人数越来越多;…………………………………………………………………………………2分
,进入园区人数多于离开人数,总人数越来越多;…………………………………………………………………………………2分
(iii)当 时, 令
时, 令 时,
时, ,
,
即在下午 点整时,园区人数达到最多.
点整时,园区人数达到最多.
此后离开人数越来越多,故园区内人数最多的时间是下午4点整. ……………2分
17.(本题满分14分)
已知圆 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ,点
,点 在直线
在直线 上,过
上,过 点作圆
点作圆 的切线
的切线 ,切点为
,切点为 .
.
(1)若 ,试求点
,试求点 的坐标;
的坐标;
(2)若 点的坐标为
点的坐标为 ,过
,过 作直线与圆
作直线与圆 交于
交于 两点,当
两点,当 时,求直线
时,求直线 的方程;
的方程;
(3)求证:经过 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
解:(1)设 ,由题可知
,由题可知 ,所以
,所以 ,解之得:
,解之得:
故所求点 的坐标为
的坐标为 或
或 . …………………………………………4分
. …………………………………………4分
(2)设直线 的方程为:
的方程为: ,易知
,易知 存在,由题知圆心
存在,由题知圆心 到直线
到直线 的距离为
的距离为 ,所以
,所以 , …………………………………………6分
, …………………………………………6分
解得, 或
或 ,
,
故所求直线 的方程为:
的方程为: 或
或 .………………………8分
.………………………8分
(3)设 ,
, 的中点
的中点 ,因为
,因为 是圆
是圆 的切线
的切线
所以经过 三点的圆是以
三点的圆是以 为圆心,以
为圆心,以 为半径的圆,
为半径的圆,
故其方程为: ……………………………10分
……………………………10分
化简得: ,此式是关于
,此式是关于 的恒等式,
的恒等式,
故 解得
解得 或
或
所以经过 三点的圆必过定点
三点的圆必过定点 或
或 .…………………………………14分
.…………………………………14分
16、证明:(1)∵

∴ ……4分
……4分
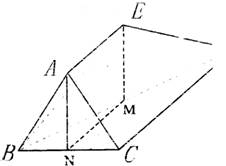 (2)令
(2)令 中点为
中点为 ,
, 中点为
中点为 ,连结
,连结 、
、
∵ 是
是 的中位线
的中位线
∴ ……6分
……6分
又∵
∴
∴ ……8分
……8分
∴
∵ 为正
为正
∴ ……10分
……10分
∴
又∵ ,
,
∴四边形 为平行四边形 ……12分
为平行四边形 ……12分
∴
∴ ……14分
……14分
16、(本题满分14分)
多面体 中,
中, ,
, ,
, ,
, 。
。
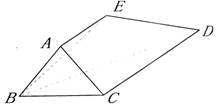 (1)求证:
(1)求证: ;
;
(2)求证: 。
。
15.(本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
已知向量
 ,且
,且 . 设
. 设 .
.
(1)求 的表达式,并求函数
的表达式,并求函数 在
在 上图像最低点
上图像最低点 的坐标.
的坐标.
(2)若对任意 ,
, 恒成立,求实数
恒成立,求实数 的范围.
的范围.
解:(1) ,即
,即 ,………………………………………………2分
,………………………………………………2分
消去 ,得
,得 ,
,
即 ,……………………………2分
,……………………………2分
 时,
时, 
 ,
, ,……………2分
,……………2分
即 的最小值为
的最小值为 ,此时
,此时
所以函数 的图像上最低点
的图像上最低点 的坐标是
的坐标是 ………………………2分
………………………2分
(2) , 即
, 即 ,
,
当 时, 函数
时, 函数 单调递增,
单调递增, 单调递增,
单调递增,
所以 在
在 上单调递增,………………………………………2分
上单调递增,………………………………………2分
所以 的最小值为1, …………………………………2分
的最小值为1, …………………………………2分
为要 恒成立,只要
恒成立,只要 ,所以
,所以 为所求.………2分
为所求.………2分
14.我们知道,如果定义在某区间上的函数 满足对该区间上的任意两个数
满足对该区间上的任意两个数 、
、 ,总有
,总有
不等式 成立,则称函数
成立,则称函数 为该区间上的向上凸函数(简
为该区间上的向上凸函数(简
称上凸). 类比上述定义,对于数列 ,如果对任意正整数
,如果对任意正整数 ,总有不等式:
,总有不等式:
 成立,则称数列
成立,则称数列 为向上凸数列(简称上凸数列). 现有数列
为向上凸数列(简称上凸数列). 现有数列 满足如下两个条件:
满足如下两个条件:
(1)数列 为上凸数列,且
为上凸数列,且 ;
;
(2)对正整数 (
( ),都有
),都有 ,其中
,其中 .
.
则数列 中的第五项
中的第五项 的取值范围为
的取值范围为  .
.
13. 已知 为圆
为圆 的两条互相垂直的弦,
的两条互相垂直的弦, 交于点
交于点 ,且
,且 ,则四边形
,则四边形 的面积等于 5 .
的面积等于 5 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com