
1.平面α内的∠MON=60°,PO是α的斜线,PO=3,∠POM=∠PON=45°,那么点P到平面α的距离是
A. 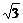 B.
B.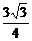 C.
C.
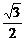 D.
D.
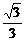
解析:cos∠POM=cos∠POH·cos∠MOH,
∴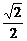 =
= 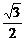 cos∠POH.
cos∠POH.
∴cos∠POH=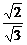 .
.
∴sin∠POH=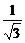 .
.
∴PH=PO·sin∠POH=3×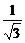 =
=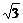 .
.
答案:A
5.设PA⊥Rt△ABC所在的平面α,∠BAC=90°,PB、PC分别与α成45°和30°角,PA=2,则PA与BC的距离是_____________;点P到BC的距离是_____________.
解析:作AD⊥BC于点D,∵PA⊥面ABC,∴PA⊥AD.∴AD是PA与BC的公垂线.易得AB=2,AC=2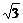 ,BC=4,AD=
,BC=4,AD=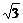 ,连结PD,则PD⊥BC,P到BC的距离PD=
,连结PD,则PD⊥BC,P到BC的距离PD=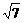 .
.
答案: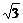
●典例剖析
[例1] 设A(2,3,1),B(4,1,2),C(6,3,7),D(-5,-4,8),求D到平面ABC的距离.
解:设平面ABC的法向量n=(x,y,z),
∵n·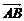 =0,n·
=0,n·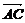 =0,
=0,
∴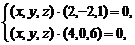
即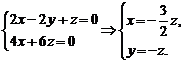
令z=-2,则n=(3,2,-2).
∴cos〈n,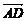 〉=
〉=
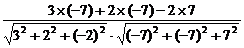 .
.
∴点D到平面ABC的距离为d,
d=|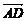 |·|cos〈n,
|·|cos〈n,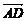 〉|=
〉|=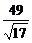 =
=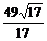 .
.
思考讨论
求点到平面的距离除了根据定义及等积变换外,还可以借用平面的法向量求得,方法是:求出平面的一个法向量n的坐标,再求出已知点P与平面内任一点M构成的向量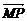 的坐标,那么P到平面的距离d=|
的坐标,那么P到平面的距离d=|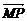 ||cos〈n,
||cos〈n,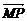 〉|.
〉|.
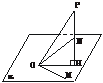
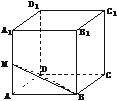
[例2] 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、O、O1分别是A1B、AC、A1C1的中点,且OH⊥O1B,垂足为H.
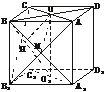
(1)求证:MO∥平面BB1C1C;
(2)分别求MO与OH的长;
(3)MO与OH是否为异面直线A1B与AC的公垂线?为什么?求这两条异面直线间的距离.
(1)证明:连结B1C,∵MO是△AB1C的中位线,∴MO∥B1C.∵B1C 平面BB1C1C,
平面BB1C1C,
∴MO∥平面BB1C1C.
(2)解:MO=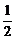 B1C=
B1C=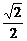 a,
a,
∵OH是Rt△BOO1斜边上的高,BO=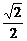 a,
a,
∴OH=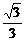 a.
a.
(3)解:MO不是A1B与AC的公垂线,MO∥B1C,△AB1C为正三角形,∴MO与AC成60°角.∵AC⊥BD,AC⊥OO1,∴AC⊥面BOO1.∵OH 面BOO1,∴OH⊥AC,OH⊥A1C1.∵OH⊥O1B,A1C1∩O1B=O1,∴OH⊥面BA1C1,OH⊥A1B.∴OH是异面直线A1B与AC的公垂线,其长度即为这两条异面直线的距离.
面BOO1,∴OH⊥AC,OH⊥A1C1.∵OH⊥O1B,A1C1∩O1B=O1,∴OH⊥面BA1C1,OH⊥A1B.∴OH是异面直线A1B与AC的公垂线,其长度即为这两条异面直线的距离.
特别提示
在立体几何的计算或证明中,常需要计算直角三角形斜边上的高,据面积关系得它等于直角边的积除以斜边,应作为常识记熟并可直接应用.立体几何问题求解,总体上可分为几何法与代数法,要注意选择最简方法求解.本题(3)利用代数向量方法解答也比较简单.
[例3] 如图所求,已知四边形ABCD、EADM和MDCF都是边长为a的正方形,点P、Q分别是ED和AC的中点.
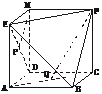
求:(1)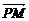 与
与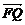 所成的角;
所成的角;
(2)P点到平面EFB的距离;
(3)异面直线PM与FQ的距离.
解:建立空间直角坐标系,使得D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)、M(0,0,a)、E(a,0,a)、F(0,a,a),则由中点坐标公式得P(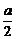 ,0,
,0,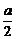 )、
)、
Q(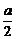 ,
,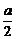 ,0).
,0).
(1)∴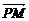 =(-
=(-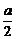 ,0,
,0,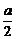 ),
),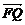 =(
=(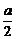 ,-
,-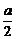 ,-a),
,-a),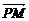 ·
·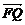 =(-
=(-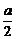 )×
)×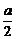 +0+
+0+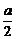 ×(-a)=-
×(-a)=-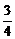 a2,且|
a2,且|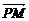 |=
|= 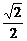 a,|
a,|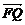 |=
|= 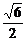 a.
a.
∴cos〈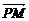 ,
,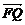 〉=
〉=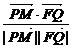 =
=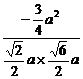 =-
=-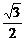 .
.
故得两向量所成的角为150°.
(2)设n=(x,y,z)是平面EFB的单位法向量,即|n|=1,n⊥平面EFB,∴n⊥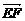 ,n⊥
,n⊥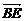 .又
.又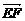 =(-a,a,0),
=(-a,a,0),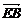 =(0,a,-a),即有
=(0,a,-a),即有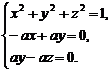 得其中的一组解
得其中的一组解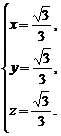 ∴n=(
∴n=(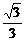 ,
,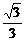 ,
,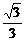 ),
),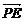 =(
=(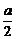 ,0,
,0,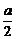 ).
).
设所求距离为d,则d=|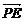 ·n|=
·n|= 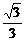 a.
a.
(3)设e=(x1,y1,z1)是两异面直线的公垂线上的单位方向向量,则由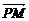 =(-
=(-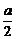 ,0,
,0,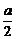 ),
),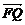 =(
=(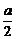 ,-
,-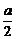 ,-a),得
,-a),得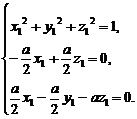 求得其中的一个e=(
求得其中的一个e=(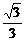 ,-
,-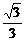 ,
,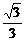 ),而
),而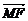 =(0,a,0).设所求距离为m,则m=|
=(0,a,0).设所求距离为m,则m=|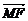 ·e|=|-
·e|=|-
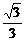 a|=
a|=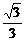 a.
a.
[例4] 如图,已知二面角α-PQ-β为60°,点A和点B分别在平面α和平面β内,点C在棱PQ上,∠ACP=∠BCP=30°,CA=CB=a.
(1)求证:AB⊥PQ;
(2)求点B到平面α的距离;
(3)设R是线段CA上的一点,直线BR与平面α所成的角为45°,求线段CR的长度.
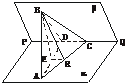
(1)证明:在平面β内作BD⊥PQ于D,连结AD.
∵∠ACP=∠BCP=30°,CA=CB=a,CD公用,∴△ACD≌△BCD.∴∠ADC=∠BDC=90°,即AD⊥PQ.于是PQ⊥平面ABD,则AB⊥PQ.
(2)解:由(1)知,∠ADB是二面角α-PQ-β的平面角,∴∠ADB=60°.又PQ⊥平面ABD,
∴α⊥平面ABD.过B作BE⊥AD于点E,则BE即为B到平面α的距离.
BE=BD·sin60°=BC·sin30°·sin60°=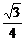 a.
a.
(3)解:连结ER,∵BE⊥α,∴∠BRE是BR与α所成的角,即∠BRE=45°,则有BR=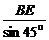 =
=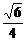 a.易知△ABD为正三角形,AB=AD=BD=
a.易知△ABD为正三角形,AB=AD=BD=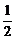 a.在△ABC中,由余弦定理得cos∠BCA=
a.在△ABC中,由余弦定理得cos∠BCA=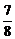 .
.
在△BCR中,设CR=x,由余弦定理得(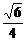 a)2=x2+a2-2ax·
a)2=x2+a2-2ax·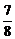 ,求得x1=
,求得x1=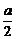 ,x2=
,x2= (舍去,∵CR<AC=a),故CR=
(舍去,∵CR<AC=a),故CR=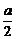 .
.
●闯关训练
夯实基础
4.A、B是直线l上的两点,AB=4,AC⊥l于A,BD⊥l于B,AC=BD=3,又AC与BD成60°的角,则C、D两点间的距离是_______.
解析:CD=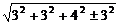 .
.
答案:5或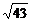
3.在棱长为a的正方体ABCD-A1B1C1D1中,M是AA1的中点,则点A1到平面MBD的距离是
A. 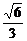 a B.
a B.
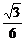 a C.
a C.
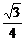 a D.
a D.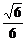 a
a
解析:A到面MBD的距离由等积变形可得.
VA-MBD=VB-AMD.易求d=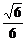 a.
a.
答案:D
2.在△ABC中,AB=15,∠BCA=120°,若△ABC所在平面α外一点P到A、B、C的距离都是14,则P到α的距离是
A.13 B.11 C.9 D.7
解析:作PO⊥α于点O,连结OA、OB、OC,
∵PA=PB=PC,
∴OA=OB=OC.
∴O是△ABC的外心.
∴OA=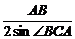 =
=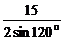 =5
=5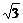 .
.
∴PO=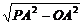 =11为所求.∴选B.
=11为所求.∴选B.
答案:B
1.ABCD是边长为2的正方形,以BD为棱把它折成直二面角A-BD-C,E是CD的中点,则异面直线AE、BC的距离为
A.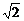 B.
B.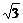 C.
C.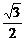 D.1
D.1
解析:易证CE是异面直线AE与BC的公垂线段,其长为所求.易证CE=1.∴选D.
答案:D
5.借助向量求距离
(1)点面距离的向量公式
平面α的法向量为n,点P是平面α外一点,点M为平面α内任意一点,则点P到平面α的距离d就是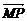 在向量n方向射影的绝对值,即d=
在向量n方向射影的绝对值,即d=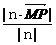 .
.
(2)线面、面面距离的向量公式
平面α∥直线l,平面α的法向量为n,点M∈α、P∈l,平面α与直线l间的距离d就是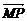 在向量n方向射影的绝对值,即d=
在向量n方向射影的绝对值,即d=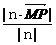 .
.
平面α∥β,平面α的法向量为n,点M∈α、P∈β,平面α与平面β的距离d就是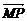 在向量n方向射影的绝对值,即d=
在向量n方向射影的绝对值,即d=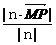 .
.
(3)异面直线的距离的向量公式
设向量n与两异面直线a、b都垂直,M∈a、P∈b,则两异面直线a、b间的距离d就是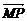 在向量n方向射影的绝对值,即d=
在向量n方向射影的绝对值,即d=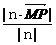 .
.
●点击双基
4.两条异面直线的公垂线段的长度叫做这两条异面直线的距离.
3.两个平面平行,它们的公垂线段的长度叫做这两个平面的距离.
2.直线与平面平行,那么直线上任一点到平面的距离叫做这条直线与平面的距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com