
3.关于平面图形的平移,主要确定的是平移向量.注意公式正、逆使用,并特别注意分清新旧函数解析式.
2.线段的定比分点的坐标表示,强化了坐标运算的应用,确定λ的值是公式应用的关键.
1.理解线段的定比分点公式时应注意以下问题:
(1)弄清起点、分点、终点,并由此决定定比λ;
(2)在计算点分有向线段所成比时,首先要确定是内分点,还是外分点,然后相应地把数量之比转化为长度之比.也可直接由定义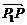 =λ
=λ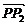 获解.
获解.
9.甲船由A岛出发向北偏东45°的方向做匀速直线航行,速度为15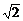 n mile/h,在甲船从A岛出发的同时,乙船从A岛正南40
n mile处的B岛出发,朝北偏东θ(θ=arctan
n mile/h,在甲船从A岛出发的同时,乙船从A岛正南40
n mile处的B岛出发,朝北偏东θ(θ=arctan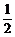 )的方向作匀速直线航行,速度为10
)的方向作匀速直线航行,速度为10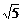 n mile/h.(如下图所示)
n mile/h.(如下图所示)
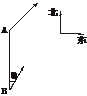
(1)求出发后3 h两船相距多少海里?
(2)求两船出发后多长时间相距最近?最近距离为多少海里?
解:以A为原点,BA所在直线为y轴建立如下图所示的坐标系.
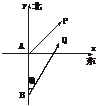
设在t时刻甲、乙两船分别在P(x1,y1),Q(x2,y2),
则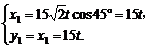
由θ=arctan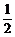 ,可得cosθ=
,可得cosθ=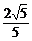 ,sinθ=
,sinθ=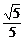 ,
,
x2=10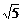 tsinθ=10t,
tsinθ=10t,
y2=10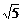 tcosθ-40=20t-40.
tcosθ-40=20t-40.
(1)令t=3,P、Q两点的坐标分别为(45,45),(30,20).
|PQ|=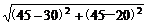 =
=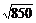 =5
=5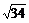 ,
,
即两船出发后3 h时,两船相距5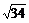 n mile.
n mile.
(2)由(1)的解法过程易知
|PQ|=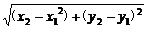
=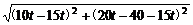
=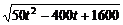
=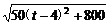 ≥20
≥20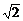 .
.
∴当且仅当t=4时,|PQ|的最小值为20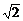 ,
,
即两船出发4 h时,相距20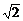 n mile为两船最近距离.
n mile为两船最近距离.
●思悟小结
8.有点难度哟!
(2004年广州综合测试)已知曲线x2+2y2+4x+4y+4=0按向量a=(2,1)平移后得到曲线C.
(1)求曲线C的方程;
(2)过点D(0,2)的直线与曲线C相交于不同的两点M、N,且M在D、N之间,设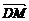 =λ
=λ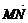 ,求实数λ的取值范围.
,求实数λ的取值范围.
解:(1)原曲线即为(x+2)2+2(y+1)2=2,则平移后的曲线C为x2+2y2=2,
即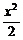 +y2=1.
+y2=1.
(2)设M(x1,y1),N(x2,y2),则
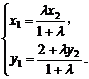 由于点M、N在椭圆x2+2y2=2上,则
由于点M、N在椭圆x2+2y2=2上,则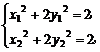
即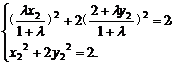
消去x22得,2λ2+8λy2+8=2λ2+4λ+2,
即y2=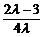 .
.
∵-1≤y2≤1,∴-1≤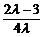 ≤1.
≤1.
又∵λ>0,故解得λ≥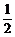 .
.
故λ的取值范围为[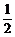 ,+∞).
,+∞).
思考讨论
本题若设出直线l的方程y=kx+2,然后与x2+2y2=2联立,利用韦达定理能求解吗?(不要忘记讨论斜率不存在的情况)读者可尝试一下.
探究创新
7.(2004年福建,17)设函数f(x)=a·b,其中a=(2cosx,1),b=(cosx,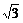 sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=1-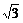 ,且x∈[-
,且x∈[-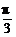 ,
,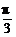 ],求x;
],求x;
(2)若y=2sin2x的图象按向量c=(m,n)(|m|<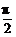 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
解:(1)依题设f(x)=2cos2x+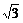 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+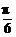 ),
),
由1+2sin(2x+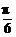 )=1-
)=1-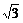 ,得
,得
sin(2x+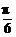 )=-
)=-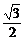 .
.
∵|x|≤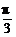 ,∴-
,∴-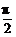 ≤2x+
≤2x+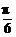 ≤
≤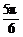 .
.
∴2x+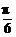 =-
=-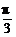 ,即x=-
,即x=-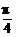 .
.
(2)函数y=2sin2x的图象按向量c=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,即y=f(x)的图象.由(1)得f(x)=2sin2(x+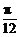 )+1.又|m|<
)+1.又|m|<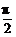 ,∴m=-
,∴m=-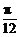 ,n=1.
,n=1.
6.已知A(2,3),B(-1,5),且满足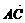 =
=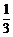
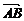 ,
,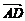 =3
=3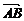 ,
,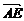 =-
=-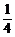
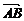 ,求C、D、E的坐标.
,求C、D、E的坐标.
解:用向量相等或定比分点坐标公式均可,读者可自行求解.C(1,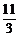 ),D(-7,9),E(
),D(-7,9),E(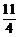 ,
,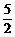 ).
).
培养能力
5.已知向量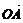 =(3,1),
=(3,1),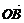 =(-1,2),
=(-1,2),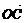 ⊥
⊥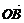 ,
,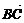 ∥
∥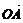 .试求满足
.试求满足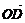 +
+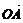 =
=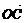 的
的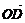 的坐标.
的坐标.
解:设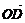 =(x,y),则
=(x,y),则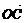 =(x,y)+(3,1)=(x+3,y+1),
=(x,y)+(3,1)=(x+3,y+1),
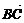 =
=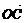 -
-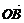 =(x+3,y+1)-(-1,2)=(x+4,y-1),
=(x+3,y+1)-(-1,2)=(x+4,y-1),
则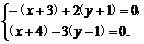
所以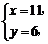
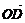 =(11,6).
=(11,6).
4.把函数y=2x2-4x+5的图象按向量a平移后,得到y=2x2的图象,且a⊥b,c=(1,-1),b·c=4,则b=____________.
解析:a=(0,0)-(1,3)=(-1,-3).设b=(x,y),由题意得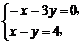
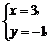
则b=(3,-1).
答案:(3,-1)
3.(2004年东城区模拟题)已知点P是抛物线y=2x2+1上的动点,定点A(0,-1),若点M分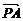 所成的比为2,则点M的轨迹方程是____________,它的焦点坐标是____________.
所成的比为2,则点M的轨迹方程是____________,它的焦点坐标是____________.
解析:设P(x0,y0),M(x,y).
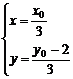
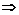
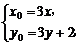 代入y0=2x02+1得3y+2=18x2+1,即18x2=3y+1,x2=
代入y0=2x02+1得3y+2=18x2+1,即18x2=3y+1,x2=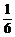 y+
y+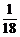 =
=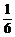 (y+
(y+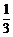 ),∴p=
),∴p=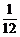 ,焦点坐标为(0,-
,焦点坐标为(0,-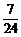 ).
).
答案:x2=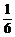 (y+
(y+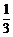 ) (0,-
) (0,-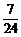 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com