
5.已知不等式|2x-t|+t-1<0的解集为(-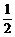 ,
,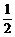 ),则t=____________.
),则t=____________.
解析:|2x-t|<1-t,t-1<2x-t<1-t,
2t-1<2x<1,t-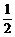 <x<
<x<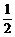 .
.
∴t=0.
答案:0
●典例剖析
[例1] 解不等式|2x+1|+|x-2|>4.
剖析:解带绝对值的不等式,需先去绝对值,多个绝对值的不等式必须利用零点分段法去绝对值求解.令2x+1=0,x-2=0,得两个零点x1=-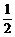 ,x2=2.
,x2=2.
解:当x≤-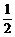 时,原不等式可化为
时,原不等式可化为
-2x-1+2-x>4,
∴x<-1.
当-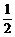 <x≤2时,原不等式可化为
<x≤2时,原不等式可化为
2x+1+2-x>4,
∴x>1.又-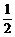 <x≤2,
<x≤2,
∴1<x≤2.
当x>2时,原不等式可化为
2x+1+x-2>4,∴x>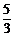 .
.
又x>2,∴x>2.
综上,得原不等式的解集为{x|x<-1或1<x}.
深化拓展
若此题再多一个含绝对值式子.如:
|2x+1|+|x-2|+|x-1|>4,你又如何去解?
分析:令2x+1=0,x-2=0,x-1=0,
得x1=-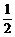 ,x2=1,x3=2.
,x2=1,x3=2.
解:当x≤-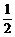 时,原不等式化为
时,原不等式化为
-2x-1+2-x+1-x>4,∴x<-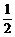 .
.
当-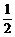 <x≤1时,原不等式可化为
<x≤1时,原不等式可化为
2x+1+2-x+1-x>4,4>4(矛盾).
当1<x≤2时,原不等式可化为
2x+1+2-x+x-1>4,∴x>1.
又1<x≤2,
∴1<x≤2.
当x>2时,原不等式可化为
2x+1+x-2+x-1>4,∴x>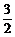 .
.
又x>2,∴x>2.
综上所述,原不等式的解集为{x|x<-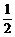 或x>1}.
或x>1}.
[例2] 解不等式|x2-9|≤x+3.
剖析:需先去绝对值,可按定义去绝对值,也可利用|x|≤a -a≤x≤a去绝对值.
-a≤x≤a去绝对值.
解法一:原不等式 (1)
(1) 或(2)
或(2)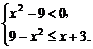
不等式(1)
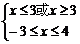
 x=-3或3≤x≤4;
x=-3或3≤x≤4;
不等式(2)

 2≤x<3.
2≤x<3.
∴原不等式的解集是{x|2≤x≤4或x=-3}.
解法二:原不等式等价于
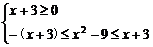

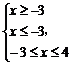 或x≥2
或x≥2 x=-3或2≤x≤4.
x=-3或2≤x≤4.
∴原不等式的解集是{x|2≤x≤4或x=-3}.
[例3] (理)已知函数f(x)=x|x-a|(a∈R).
(1)判断f(x)的奇偶性;
(2)解关于x的不等式:f(x)≥2a2.
解:(1)当a=0时,
f(-x)=-x|-x|=-x|x|=-f(x),
∴f(x)是奇函数.
当a≠0时,f(a)=0且f(-a)=-2a|a|.
故f(-a)≠f(a)且f(-a)≠-f(a).
∴f(x)是非奇非偶函数.
(2)由题设知x|x-a|≥2a2,
∴原不等式等价于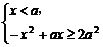 ①
①
或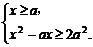 ②
②
由①得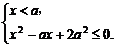 x∈
x∈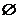 .
.
由②得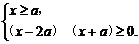
当a=0时,x≥0.
当a>0时,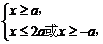
∴x≥2a.
当a<0时,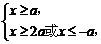
即x≥-a.
综上
a≥0时,f(x)≥2a2的解集为{x|x≥2a};
a<0时,f(x)≥2a2的解集为{x|x≥-a}.
(文)设函数f(x)=ax+2,不等式| f(x)|<6的解集为(-1,2),试求不等式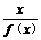 ≤1的解集.
≤1的解集.
解:|ax+2|<6,
∴(ax+2)2<36,
即a2x2+4ax-32<0.
由题设可得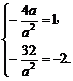
解得a=-4.
∴f(x)=-4x+2.
由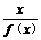 ≤1,即
≤1,即 ≤1可得
≤1可得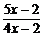 ≥0.
≥0.
解得x>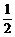 或x≤
或x≤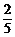 .
.
∴原不等式的解集为{x|x>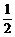 或x≤
或x≤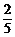 }.
}.
●闯关训练
夯实基础
4.已知不等式a≤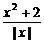 对x取一切负数恒成立,则a的取值范围是____________.
对x取一切负数恒成立,则a的取值范围是____________.
解析:要使a≤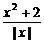 对x取一切负数恒成立,
对x取一切负数恒成立,
令t=|x|>0,则a≤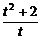 .
.
而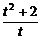 ≥
≥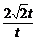 =2
=2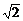 ,
,
∴a≤2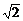 .
.
答案:a≤2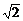
3.不等式|x+log3x|<|x|+|log3x|的解集为
A.(0,1) B.(1,+∞)
C.(0,+∞) D.(-∞,+∞)
解析:∵x>0,x与log3x异号,
∴log3x<0.∴0<x<1.
答案:A
2.(2004年春季安徽)不等式|2x2-1|≤1的解集为
A.{x|-1≤x≤1} B.{x|-2≤x≤2}
C.{x|0≤x≤2} D.{x|-2≤x≤0}
解析:由|2x2-1|≤1得-1≤2x2-1≤1.
∴0≤x2≤1,即-1≤x≤1.
答案:A
1.(2003年成都第三次诊断题)设a、b是满足ab<0的实数,那么
A.|a+b|>|a-b|
B.|a+b|<|a-b|
C.|a-b|<||a|-|b||
D.|a-b|<|a|+|b|
解析:用赋值法.令a=1,b=-1,代入检验.
答案:B
2.绝对值不等式的性质中等号成立的条件是什么?
●点击双基
1.在|x|>a x>a或x<-a(a>0)、|x|<a
x>a或x<-a(a>0)、|x|<a -a<x<a(a>0)中的a>0改为a∈R还成立吗?
-a<x<a(a>0)中的a>0改为a∈R还成立吗?
4.绝对值不等式的性质:
||a|-|b||≤|a±b|≤|a|+|b|.
思考讨论
3.含参不等式的求解,通常对参数分类讨论.
2.形如|x-a|+|x-b|≥c的不等式的求解通常采用“零点分段讨论法”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com