
1.若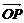 =xi+yj+zk,那么(x,y,z)叫做向量
=xi+yj+zk,那么(x,y,z)叫做向量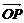 的坐标,也叫点P的坐标.
的坐标,也叫点P的坐标.
9.7 空间向量及其坐标运算(B)
●知识梳理
2.空间中的任何一个向量都可以用不共面的三个向量线性表示,这三个向量也称为一个基底.在证明两个向量平行、垂直或求其夹角时,往往把它们用同一个基底来表示,从而实现解题的目的.
拓展题例
[例1] 下列命题中不正确的命题个数是
①若A、B、C、D是空间任意四点,则有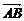 +
+ +
+  +
+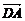 =0 ②|a|-|b|=|a+b|是a、b共线的充要条件
③若a、b共线,则a与b所在直线平行 ④对空间任意点O与不共线的三点A、B、C,若
=0 ②|a|-|b|=|a+b|是a、b共线的充要条件
③若a、b共线,则a与b所在直线平行 ④对空间任意点O与不共线的三点A、B、C,若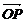 =x
=x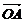 +y
+y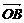 +z
+z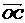 (其中x、y、z∈R),则P、A、B、C四点共面
(其中x、y、z∈R),则P、A、B、C四点共面
A.1 B.2 C.3 D.4
解析:易知只有①是正确的,对于④,若O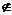 平面ABC,则
平面ABC,则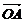 、
、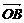 、
、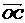 不共面,由空间向量基本定理知,P可为空间任一点,所以P、A、B、C四点不一定共面.
不共面,由空间向量基本定理知,P可为空间任一点,所以P、A、B、C四点不一定共面.
答案:C
[例2] A是△BCD所在平面外一点,M、N分别是△ABC和△ACD的重心,若BD=4,试求MN的长.
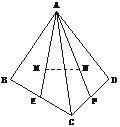
解:连结AM并延长与BC相交于E,连结AN并延长与CD相交于E,则E、F分别是BC及CD的中点.
现在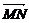 =
=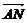 -
-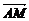 =
=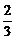
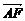 -
-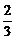
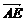 =
=  (
(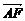 -
-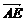 )=
)=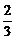
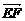 =
= 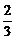 (
(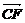 -
-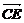 )=
)=
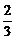 (
(
 -
- 
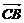 )=
)=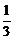 (
( -
-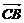 )=
)=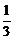
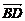 .
.
∴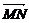 =|
=|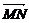 |=
|= 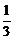 |
|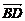 |=
|= 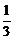 BD=
BD=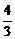 .
.
说明:本题的关键是利用重心这一特殊位置逐步进行转化.
[例3] 设A、B、C及A1、B1、C1分别是异面直线l1、l2上的三点,而M、N、P、Q分别是线段AA1、BA1、BB1、CC1的中点.求证:M、N、P、Q四点共面.
证明: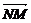 =
= 
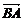 ,
,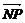 =
= 
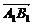 ,
,
∴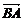 =2
=2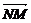 ,
,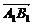 =2
=2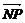 .
.
又∵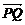 =
=  (
( +
+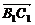 ), (*)
), (*)
A、B、C及A1、B1、C1分别共线,
∴ =λ
=λ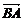 =2
=2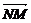 ,
,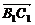 =ω
=ω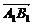 =2ω
=2ω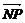 .
.
代入(*)式得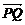 =
=  (2λ
(2λ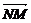 +2ω
+2ω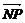 )=λ
)=λ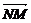 +ω
+ω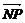 ,∴
,∴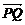 、
、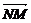 、
、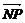 共面.
共面.
∴M、N、P、Q四点共面.
1.要使学生正确理解空间向量的加法法则、减法法则以及空间向量的数量积,掌握空间向量平行、垂直的条件及三个向量共面及四点共面的条件.
2.应用向量知识解决几何问题时,一方面要选择恰当的基向量,另一方面要熟练地进行向量运算.
●教师下载中心
教学点睛
1.若表示向量a1,a2,…,an的有向线段终点和始点连结起来构成一个封闭折图形,则a1+a2+a3+…+an=0.
8.(2004年全国Ⅰ,理20)如下图,已知四棱锥P-ABCD,PB⊥AD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.
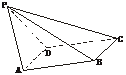
(1)求点P到平面ABCD的距离;
(2)求面APB与面CPB所成二面角的大小.
(1)解:如下图,作PO⊥平面ABCD,垂足为点O.连结OB、OA、OD,OB与AD交于点E,连结PE.
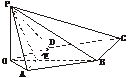
∵AD⊥PB,∴AD⊥OB.∵PA=PD,∴OA=OD.
于是OB平分AD,点E为AD的中点,∴PE⊥AD.由此知∠PEB为面PAD与面ABCD所成二面角的平面角,∴∠PEB=120°,∠PEO=60°.由已知可求得PE=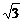 ,∴PO=PE·sin60°=
,∴PO=PE·sin60°=
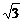 ×
×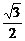 =
=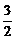 ,即点P到平面ABCD的距离为
,即点P到平面ABCD的距离为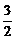 .
.
(2)解法一:如下图建立直角坐标系,其中O为坐标原点,x轴平行于DA.
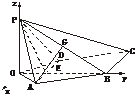
P(0,0,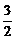 ),B(0,
),B(0,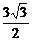 ,0),PB中点G的坐标为(0,
,0),PB中点G的坐标为(0,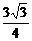 ,
,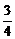 ),连结AG.
),连结AG.
又知A(1,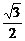 ,0),C(-2,
,0),C(-2,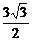 ,0).
,0).
由此得到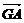 =(1,-
=(1,-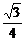 ,-
,-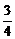 ),
),
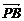 =(0,
=(0,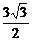 ,-
,-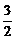 ),
), =(-2,0,0).
=(-2,0,0).
于是有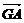 ·
·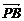 =0,
=0, ·
·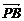 =0,
=0,
∴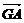 ⊥
⊥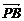 ,
, ⊥
⊥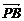 .
.
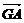 ,
, 的夹角θ等于所求二面角的平面角.
的夹角θ等于所求二面角的平面角.
于是cosθ=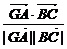 =-
=-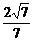 ,
,
∴所求二面角的大小为π-arccos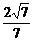 .
.
解法二:如下图,取PB的中点G,PC的中点F,连结EG、AG、GF,则AG⊥PB,FG∥
BC,FG= BC.
BC.
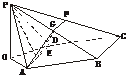
∵AD⊥PB,∴BC⊥PB,FG⊥PB.∴∠AGF是所求二面角的平面角.
∵AD⊥面POB,∴AD⊥EG.
又∵PE=BE,∴EG⊥PB,且∠PEG=60°.
在Rt△PEG中,EG=PE·cos60°=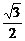 ,
,
在Rt△GAE中,AE= AD=1,于是tan∠GAE=
AD=1,于是tan∠GAE=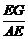 =
= 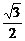 .
.
又∠AGF=π-∠GAE,
∴所求二面角的大小为π-arctan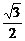 .
.
●思悟小结
7.在空间四边形ABCD中,求证: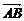 ·
· +
+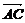 ·
·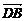 +
+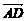 ·
· =0.
=0.
证法一:把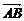 拆成
拆成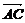 +
+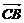 后重组,
后重组,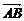 ·
· +
+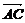 ·
·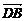 +
+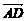 ·
· =(
=(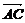 +
+
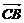 )·
)· +
+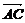 ·
·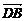 +
+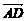 ·
· =
=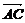 ·
· +
+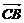 ·
· +
+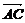 ·
·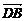 +
+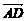 ·
· =
=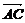 ·(
·( +
+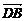 )+
)+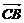 ·(
·( +
+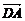 )=
)=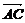 ·
·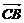 +
+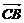 ·
·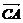 =
= 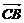 ·(
·(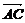 +
+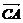 )=
)=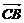 ·0=0.
·0=0.
证法二:如下图,设a=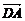 ,b=
,b= 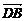 ,c=
,c=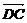 ,则
,则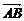 ·
· +
+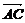 ·
·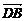 +
+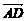 ·
· =(b-a)·(-c)+(c-a)·b+(-a)·(c-b)=-b·c+a·c+c·b-a·b-a·c+a·b=0.
=(b-a)·(-c)+(c-a)·b+(-a)·(c-b)=-b·c+a·c+c·b-a·b-a·c+a·b=0.
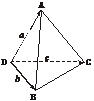
评述:把平面向量的运算推广到空间后,许多基本的运算规则没有变.证法一中体现了向量的拆分重组技巧,要求较高;证法二设定三个向量为基底,而原式中所有向量化归为关于a、b、c的式子,化简时的思路方向较清楚.
探究创新
6.沿着正四面体OABC的三条棱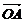 、
、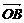 、
、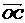 的方向有大小等于1、2、3的三个力f1、f2、f3.试求此三个力的合力f的大小以及此合力与三条棱所夹角的余弦.
的方向有大小等于1、2、3的三个力f1、f2、f3.试求此三个力的合力f的大小以及此合力与三条棱所夹角的余弦.
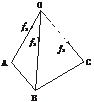
解:用a、b、c分别代表棱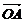 、
、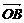 、
、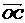 上的三个单位向量,则f1=a,f2=2b,f3=3c,则f=f1+f2+f3=a+2b+3c,
上的三个单位向量,则f1=a,f2=2b,f3=3c,则f=f1+f2+f3=a+2b+3c,
∴|f|2=(a+2b+3c)·(a+2b+3c)=|a|2+4|b|2+9|c|2+4a·b+6a·c+12b·c=1+4+9+4|a||b|cos〈a,b〉
+6|a||c|cos〈a,c〉+12|b||c|cos〈b,c〉=14+4cos60°+6cos60°+12cos60°=14+2+3+6=25.
∴|f|=5,即所求合力的大小为5,
且cos〈f,a〉= =
=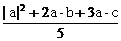 =
=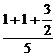 =
=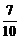 .
.
同理,可得cos〈f,b〉=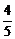 ,cos〈f,c〉=
,cos〈f,c〉=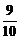 .
.
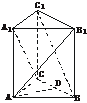
5.直三棱柱ABC-A1B1C1中,BC1⊥AB1,BC1⊥A1C,求证:AB1=A1C.
证明:∵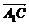 =
=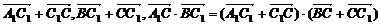 =
=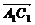 ·
·
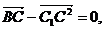
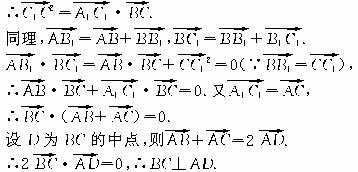
∴AB=AC.又A1A=B1B,∴A1C=AB1.
评述:本题在利用空间向量来解决位置关系问题时,要用到空间多边形法则、向量的运算、数量积以及平行、相等和垂直的条件.
培养能力
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com