
2、背诵故事的高潮三、四段。
教学难点
理解“因、如、举、谢、意”等五个多义词义项,掌握两个句式。
教具准备:投影。
课时安排:4课时
教学步骤
第一课时
1、分析“项羽”这个主要的人物形象。
3、背诵课文第三、四段。
教学重点
2、归纳总结“因、如、举、谢、意”五个多义词的义项;了解“此……也(耳)”“何以……”两个句式的特点,并比较与现代汉语的不同。
《鸿门宴》4课时、《陈情表》3课时、《段太尉逸事状》4课时、《游褒禅山记》3课时、《郑伯克段于鄢》3课时、《报任安书》3课时.
鸿门宴
教学目标
1、了解作者对项羽悲剧性格的揭示,体会人物的性格特点在其政治、军事生涯众所起的重要作用。
领悟并鉴赏古代实用类文言文的语言艺术、表意方式和写作方法。
3.向量法是把距离求解转化为向量运算.
●教师下载中心
教学点睛
首先要让学生理解点到平面的距离、异面直线的距离以及线面距离及面面距离,而后结合题目向学生总结求距离的常用方法,如:直接法、转化法、向量法.对异面直线的距离只要求学生掌握作出公垂线段或用向量表示的情况.
拓展题例
[例1] 线段AB与平面α平行,α的斜线A1A、B1B与α所成的角分别为30°和60°,且∠A1AB=∠B1BA=90°,AB=6,A1B1=10,求AB与平面α的距离.
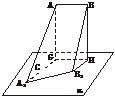
解:如图,作AG⊥α于点G,BH⊥α于点H,连结A1G、B1H、GH,因为A1A⊥AB,A1G⊥GH.同理,B1H⊥GH.作B1C⊥A1G于点C,则B1C=GH=AB=6,∠AA1G=30°,∠BB1H=60°.设B1H=x,则CG=B1H=x,AG=BH=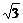 x,A1G=3x=x+A1C=x+8.
x,A1G=3x=x+A1C=x+8.
所以x=4,AG=BH=4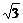 .当A1、B1分居平面AH两侧时,类似可得AG=BH=2
.当A1、B1分居平面AH两侧时,类似可得AG=BH=2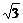 .
.
[例2] (2003年烟台诊断性测试)如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点.
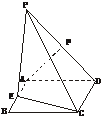
(1)求证:AF∥平面PCE;
(2)若二面角P-CD-B为45°,求证:平面PCE⊥平面PCD;
(3)在(2)的条件下,若AD=2,CD=2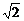 ,求F到平面PCE的距离.
,求F到平面PCE的距离.
(1)证明:如下图,取PC的中点为M,连结EM、FM. 由
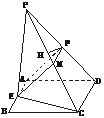
|
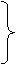 FM
FM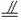
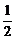 CD
CD
AE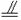
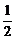 CD
CD
|
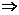 AF∥EM
AF∥EM
EM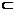 面PCE
面PCE
AF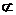 面PCE
面PCE
(2)证明: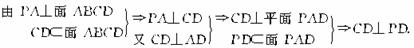
则∠PDA为二面角P-CD-B的平面角.
∠PDA=45°,故△PAD为等腰Rt△.
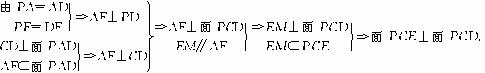
(3)作FH⊥PC,
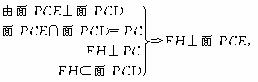
即FH为点F到面PCE的距离.
由AD=2可得PD=2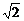 ,又由CD=2
,又由CD=2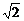 ,
,
则有PC=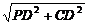 =4.
=4.
又由Rt△PHF∽Rt△PDC,则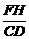 =
=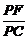
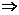
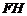 =
=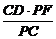 =
=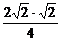 =1.
=1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com