
3.对“线线垂直”“线面垂直”及“面面垂直”之间的关系作系统小结.
拓展题例
[例1] 已知m、l是直线,α、β是平面,给出下列命题:①若l垂直于α内两条相交直线,则l⊥α;②若l平行于α,则l平行于α内所有的直线;③若m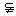 α,l
α,l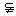 β且l⊥m,则α⊥β;④若l
β且l⊥m,则α⊥β;④若l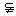 β且l⊥α,则α⊥β;⑤若m
β且l⊥α,则α⊥β;⑤若m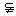 α,l
α,l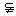 β且α∥β,则l∥m.其中正确命题的序号是_____________.
β且α∥β,则l∥m.其中正确命题的序号是_____________.
答案:①④
[例2] 如图,AB是圆O的直径,C是圆周上一点,PA⊥平面ABC.
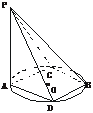
(1)求证:平面PAC⊥平面PBC;
(2)若D也是圆周上一点,且与C分居直径AB的两侧,试写出图中所有互相垂直的各对平面.
(1)证明:∵C是AB为直径的圆O的圆周上一点,
∴BC⊥AC.
又PA⊥平面ABC,BC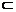 平面ABC,
平面ABC,
∴BC⊥PA,从而BC⊥平面PAC.
∵BC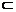 平面PBC,
平面PBC,
∴平面PAC⊥平面PBC.
(2)解:平面PAC⊥平面ABCD;
平面PAC⊥平面PBC;
平面PAD⊥平面PBD;
平面PAB⊥平面ABCD;
平面PAD⊥平面ABCD.
[例3] 如下图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,又二面角P-CD-B为45°.
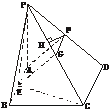
(1)求证:AF∥平面PEC;
(2)求证:平面PEC⊥平面PCD;
(3)设AD=2,CD=2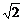 ,求点A到平面PEC的距离.
,求点A到平面PEC的距离.
分析:对问题(1),关键是证明AF与平面PEC内的一条直线平行,为此可取PC的中点G,论证AF∥EG;对问题(2),可转化为证明线面垂直;对问题(3),可转化为求点F到平面PEC的距离,进而可以充分运用(2)的结论.
(1)证明:取PC的中点G,连结EG、FG.
∵F是PD的中点,∴FG∥CD且FG=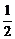 CD.而AE∥CD且AE=
CD.而AE∥CD且AE=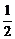 CD,∴EA∥GF且EA=GF,故四边形EGFA是平行四边形,从而EG∥AF.又AF
CD,∴EA∥GF且EA=GF,故四边形EGFA是平行四边形,从而EG∥AF.又AF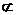 平面PEC,EG
平面PEC,EG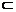 平面PEC,∴AF∥平面PEC.
平面PEC,∴AF∥平面PEC.
(2)证明:∵PA⊥平面ABCD,∴AD是PD在平面ABCD上的射影.又CD⊥AD,∴CD⊥
PD,∠PDA就是二面角P-CD-B的平面角.∴∠ADP=45°,则AF⊥PD.
又AF⊥CD,PD∩CD=D,∴AF⊥平面PCD.
由(1),EG∥AF,∴EG⊥平面PCD,
而EG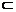 平面PEC,∴平面PEC⊥平面PCD.
平面PEC,∴平面PEC⊥平面PCD.
(3)解:过F作FH⊥PC交PC于点H,又平面PEC⊥平面PCD,则FH⊥平面PEC,∴FH为点F到平面PEC的距离,而AF∥平面PEC,故FH等于点A到平面PEC的距离.
在△PFH与△PCD中,
∵∠FHP=∠CDP=90°,∠FPC为公共角,
∴△PFH∽△PCD,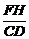 =
=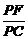 .
.
∵AD=2,CD=2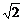 ,PF=
,PF=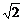 ,PC=
,PC=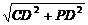 =4,∴FH=
=4,∴FH=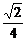 ·2
·2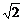 =1.
=1.
∴点A到平面PEC的距离为1.
2.在作二面角的平面角时,往往利用两个平面垂直的性质定理,即从某个平面内一点作它们交线的垂线,从而与另一个平面垂直,再作二面角、棱的垂线,由三垂线定理的逆定理得两垂足的连线也垂直于棱.
1.结合图形向学生讲明两个平面垂直的判定定理及性质定理.
9.如下图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°,且边长为a的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.
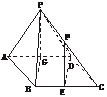
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)求二面角A-BC-P的大小;
(4)若E为BC边的中点,能否在棱PC上找一点F,使得平面DEF⊥平面ABCD,并证明你的结论.
(1)证明:∵在菱形ABCD中,∠DAB=60°,G为AD边的中点,∴BG⊥AD.又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴BG⊥平面PAD.
(2)证明:连结PG,则PG⊥AD,由(1)得BG⊥AD,又PG∩BG=G,BG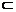 平面PBG,PG
平面PBG,PG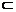 平面PBG,∴AD⊥平面PBG,PB
平面PBG,∴AD⊥平面PBG,PB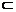 平面PBG.∴AD⊥PB.
平面PBG.∴AD⊥PB.
(3)解:由(2)AD⊥平面PBG,而BC∥AD,∴BC⊥平面PBG.而PB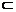 平面PBG,BG
平面PBG,BG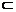 平面PBG,∴BC⊥PB,BC⊥BG.∴∠PBG就是二面角A-BC-P的平面角.
平面PBG,∴BC⊥PB,BC⊥BG.∴∠PBG就是二面角A-BC-P的平面角.
在△PAD中,PG=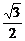 a,∴在△PGB中,∠PBG=45°,即二面角A-BC-P为45°.
a,∴在△PGB中,∠PBG=45°,即二面角A-BC-P为45°.
(4)解:当F为PC的中点时,满足平面DEF⊥平面ABCD.证明如下:
取PC的中点F,连结DE、EF、DF,则由平面几何知识,在△PBC中,EF∥PB,在菱形ABCD中,GB∥DE,而EF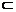 平面DEF,ED
平面DEF,ED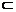 平面DEF,EF∩DE=E,∴平面DEF∥平面PGB.又PG⊥平面ABCD,而PG
平面DEF,EF∩DE=E,∴平面DEF∥平面PGB.又PG⊥平面ABCD,而PG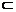 平面PGB,∴平面PGB⊥平面ABCD.故平面DEF⊥平面ABCD.
平面PGB,∴平面PGB⊥平面ABCD.故平面DEF⊥平面ABCD.
评述:本题第(1)问的论证中主要运用了面面垂直的性质定理,第(2)问通过线线垂直与线面垂直的转化得以证明,第(3)问是通过寻找与二面角的棱垂直的平面,进而得出二面角的平面角,再归结为论证与计算,第(4)问是探索性问题,这里通过直觉捕捉结果,再进行逻辑论证.
●思悟小结
在证明两平面垂直时,一般方法是先从现有的直线中寻找平面的垂线,若没有这样的直线,则可通过作辅助线来解决,而作辅助线则应有理论根据并且要有利于证明,不能随意添加.在有平面垂直时,一般要用性质定理,在一个平面内作交线的垂线,使之转化为线面垂直.解决这类问题的关键是熟练掌握“线线垂直”“线面垂直”“面面垂直”间的转化条件和转化应用.
●教师下载中心
教学点睛
8.(2003年杭州高考质量检测题)如下图,在正三棱柱ABC-A1B1C1中,AB=AA1,E是棱BB1的中点.
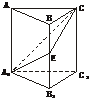
(1)求证:平面A1EC⊥平面AA1C1C;
(2)若我们把平面A1EC与平面A1B1C1所成的锐二面角为60°时的正三棱柱称为“黄金棱柱”,请判断此三棱柱是否为“黄金棱柱”,并说明理由;
(3)设AB=a,求体积V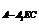 .
.
(1)证明:连结A1C与AC1交于点F,连结EF,则由条件可得EC=EA1,则EF⊥A1C.同理EC1=EA,则EF⊥AC1,∴EF⊥面AA1C1C.
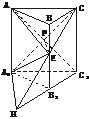
而EF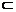 面A1EC,所以平面A1EC⊥平面AA1C1C.
面A1EC,所以平面A1EC⊥平面AA1C1C.
(也可通过如下(2)的辅助线先证明EF∥A1H,而A1H⊥面AA1C1C得到)
(2)解:延长CE交C1B1的延长线于点H,则有C1B1=B1H=A1B1,则∠HA1C1=90°,且∠CA1H=90°,所以∠CA1C1为平面A1EC与平面A1B1C1所成二面角的平面角.若此正三棱柱为“黄金棱柱”,则∠CA1C1=60°,应有CC1=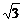 A1C1,与条件AB=AA1矛盾.
A1C1,与条件AB=AA1矛盾.
所以此三棱柱不能成为“黄金棱柱”.
(也可利用公式cosθ=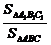 得到二面角的平面角来解决)
得到二面角的平面角来解决)
(3)解:V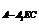 =V
=V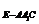 =
=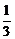 ·EF·
·EF·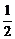 AA1·AC=
AA1·AC=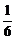 ×
×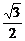 a×a×a=
a×a×a=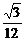 a3.
a3.
(或通过V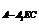 =V
=V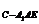 来计算)
来计算)
探究创新
7.如下图,四棱锥P-ABCD的底面是边长为a的正方形,PA⊥底面ABCD,E为AB的中点,且PA=AB.
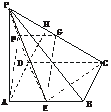
(1)求证:平面PCE⊥平面PCD;
(2)求点D到平面PCE的距离.
(1)证明:取PD的中点F,则AF⊥PD.
∵CD⊥平面PAD,∴AF⊥CD.
∴AF⊥平面PCD.
取PC的中点G,连结EG、FG,可证AFGE为平行四边形.
∴AF∥EG.∴EG⊥平面PCD.
∵EG在平面PCE内,
∴平面PCE⊥平面PCD.
(2)解:在平面PCD内,过点D作DH⊥PC于点H.
∵平面PCE⊥平面PCD,∴DH⊥平面PCE,即DH为点D到平面PCE的距离.
在Rt△PAD中,PA=AD=a,PD=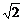 a.
a.
在Rt△PCD中,PD=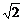 a,CD=a,PC=
a,CD=a,PC=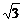 a,
a,
∴DH=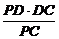 =
=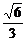 a.
a.
6.(文)如下图,正四棱柱ABCD-A1B1C1D1中,底面边长为2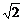 ,侧棱长为4,E、F分别为棱AB、BC的中点,EF∩BD=G.
,侧棱长为4,E、F分别为棱AB、BC的中点,EF∩BD=G.
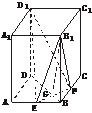
(1)求证:平面B1EF⊥平面BDD1B;
(2)求点D1到平面B1EF的距离d;
(3)求三棱锥B1-EFD1的体积V.
(1)证法一:如下图,连结AC.
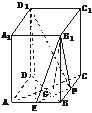
∵正四棱柱ABCD-A1B1C1D1的底面是正方形,
∴AC⊥BD.又AC⊥D1D,故AC⊥平面BDD1B1.
∵E、F分别为AB、BC的中点,故EF∥AC.
∴EF⊥平面BDD1B1.
∴平面B1EF⊥平面BDD1B1.
证法二:∵BE=BF,∠EBD=∠FBD=45°,∴EF⊥BD.
又EF⊥D1D,∴EF⊥平面BDD1B1.
∴平面B1EF⊥平面BDD1B1.
(2)解:在对角面BDD1B1中,作D1H⊥B1G,垂足为H.
∵平面B1EF⊥平面BDD1B1,
且平面B1EF∩平面BDD1B1=B1G,
∴D1H⊥平面B1EF,且垂足为H.
∴点D1到平面B1EF的距离d=D1H.
在Rt△D1HB1中,D1H=D1B1·sin∠D1B1H.
∵D1B1=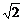 A1B1=
A1B1=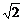 ·2
·2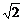 =4,sin∠D1B1H=sin∠B1GB=
=4,sin∠D1B1H=sin∠B1GB=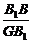 =
=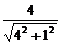 =
=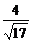 ,
,
∴d=D1H=4·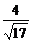 =
=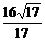 .
.
(3)解:V=V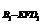 =V
=V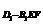 =
=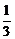 ·d·S
·d·S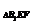 =
=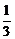 ·
·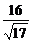 ·
·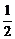 ·2·
·2·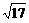 =
=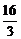 .
.
评注:近几年立体几何的解答题一般都是一题多问,环环相扣.如本题的三小问便是如此.本题主要考查正四棱柱等基本知识,考查逻辑推理能力及空间思维能力.
(理)如下图,正方体ABCD-A1B1C1D1中,棱长为a.求:
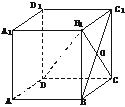
(1)AB与B1C所成的角;
(2)AB与B1C间的距离;
(3)AB与B1D间的距离.
解:(1)∵AB∥CD,
∴∠B1CD是AB与B1C所成角.
∵DC⊥平面BB1C1C,
∴DC⊥B1C.于是∠DCB1=90°.
∴AB与B1C所成角为90°.
(2)连结BC1交B1C于O,则BO⊥B1C.
又AB⊥平面BB1C1C,∴AB⊥BO.
∴BO是异面直线AB和B1C的公垂线段,
易得BO=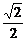 a,
a,
即AB与B1C间的距离为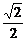 a.
a.
(3)∵AB∥DC,AB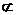 平面B1DC,DC
平面B1DC,DC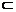 平面B1DC,∴AB∥平面B1DC,从而AB与平面B1DC间的距离即为AB与B1D间的距离.
平面B1DC,∴AB∥平面B1DC,从而AB与平面B1DC间的距离即为AB与B1D间的距离.
∵BO⊥B1C,BO⊥CD,B1C∩DC=C,
∴BO⊥平面DB1C.∴BO的长为B到平面B1DC间的距离.
∵BO=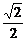 a,∴AB与B1D间的距离为
a,∴AB与B1D间的距离为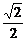 a.
a.
培养能力
5.在长方体ABCD-A1B1C1D1中,底面ABCD是边长为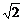 的正方形,侧棱长为
的正方形,侧棱长为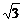 ,E、F分别是AB1、CB1的中点,求证:平面D1EF⊥平面AB1C.
,E、F分别是AB1、CB1的中点,求证:平面D1EF⊥平面AB1C.
证明:如下图,∵E、F分别是AB1、CB1的中点,
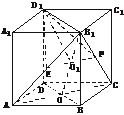
∴EF∥AC.
∵AB1=CB1,
O为AC的中点,
∴B1O⊥AC.
故B1O⊥EF.
在Rt△B1BO中,∵BB1=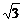 ,BO=1,
,BO=1,
∴∠BB1O=30°.从而∠OB1D1=60°,又B1D1=2,B1O1=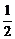 OB1=1(O1为BO与EF的交点).
OB1=1(O1为BO与EF的交点).
∴△D1B1O1是直角三角形,即B1O⊥D1O1.
∴B1O⊥平面D1EF.又B1O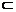 平面ACB1,
平面ACB1,
∴平面D1EF⊥平面AB1C.
4.三个平面两两互相垂直,它们的三条交线交于一点O,P到三个平面的距离分别是3、4、5,则OP的长为__________.
解析:构造棱长分别为3、4、5的长方体,使OP为长方体的对角线.
故OP=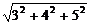 =5
=5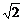 .
.
答案:5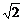
3.设a、b是异面直线,α、β是两个平面,且a⊥α,b⊥β,a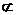 β,b
β,b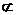 α,则当__________(填上一种条件即可)时,有α⊥β.
α,则当__________(填上一种条件即可)时,有α⊥β.
解析:本题为开放性问题.可以填上a⊥b,也可以填a∥β,或b∥α.
答案:a⊥b
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com