
9.(2005年北京西城区抽样测试)已知sin2α= ,α∈(
,α∈(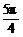 ,
, ).
).
(1)求cosα的值;
(2)求满足sin(α-x)-sin(α+x)+2cosα=-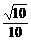 的锐角x.
的锐角x.
解:(1)因为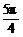 <α<
<α< ,
,
所以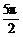 <2α<3π.
<2α<3π.
所以cos2α=-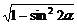 =-
=-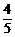 .
.
由cos2α=2cos2α-1,所以cosα=-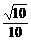 .
.
(2)因为sin(α-x)-sin(α+x)+2cosα=-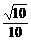 ,
,
所以2cosα(1-sinx)=-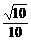 .
.
所以sinx=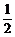 .
.
因为x为锐角,所以x=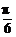 .
.
探究创新
8.已知sinβ=msin(2α+β)(m≠1),求证:tan(α+β)=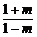 tanα.
tanα.
证明:∵sinβ=msin(2α+β),
∴sin[(α+β)-α]=msin[(α+β)+α].
∴sin(α+β)cosα-cos(α+β)sinα
=msin(α+β)cosα+mcos(α+β)sinα.
∴(1-m)sin(α+β)cosα
=(1+m)cos(α+β)sinα.
∴tan(α+β)=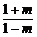 tanα.
tanα.
7.已知sin( -x)=
-x)=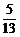 ,0<x<
,0<x< ,求
,求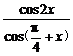 的值.
的值.
分析:角之间的关系:( -x)+(
-x)+( +x)=
+x)=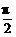 及
及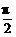 -2x=2(
-2x=2( -x),利用余角间的三角函数的关系便可求之.
-x),利用余角间的三角函数的关系便可求之.
解:∵( -x)+(
-x)+( +x)=
+x)=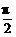 ,
,
∴cos( +x)=sin(
+x)=sin( -x).
-x).
又cos2x=sin(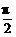 -2x)
-2x)
=sin2( -x)=2sin(
-x)=2sin( -x)cos(
-x)cos( -x),
-x),
∴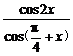 =2cos(
=2cos( -x)=2×
-x)=2× =
=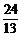 .
.
6.已知cosα=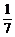 ,cos(α+β)=-
,cos(α+β)=-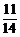 ,α、β∈(0,
,α、β∈(0,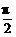 ),求β.
),求β.
解:由cosα=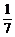 ,cos(α+β)=-
,cos(α+β)=-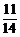 ,
,
得cosβ=cos[(α+β)-α]=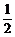 ,
,
得β= .
.
培养能力
5.(2004年湖南,17)已知tan( +α)=2,求
+α)=2,求 的值.
的值.
解:由tan( +α)=
+α)=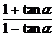 =2,
=2,
得tanα=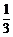 .
.
于是 =
=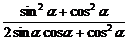 =
=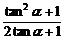 =
=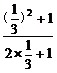 =
=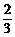 .
.
4.在△ABC中,若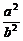 =
=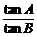 ,则△ABC的形状为_______.
,则△ABC的形状为_______.
解析:左边利用正弦定理,右边“切变弦”,原式可化为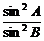 =
=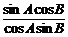
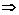
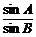 =
=
sin2A=sin2B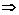 2A=2B或2A=π-2B
2A=2B或2A=π-2B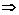 A=B或A+B=
A=B或A+B=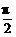 .
.
答案:等腰三角形或直角三角形
3.(2004年福建,2)tan15°+cot15°等于
A.2 B.2+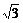 C.4 D.
C.4 D.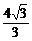
解析一:tan15°+cot15°=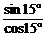 +
+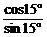 =
=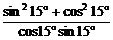 =
=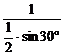 =4.
=4.
解析二:由tan15°=tan(45°-30°)=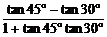 =
=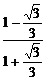 =
=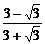 .
.
∴原式=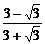 +
+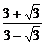 =4.
=4.
答案:C
2.要使sinα-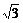 cosα=
cosα=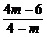 有意义,则应有
有意义,则应有
A.m≤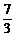 B.m≥-1
B.m≥-1
C.m≤-1或m≥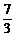 D.-1≤m≤
D.-1≤m≤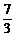
解析:2sin(α- )=
)=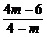
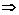 sin(α-
sin(α- )=
)=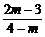 .
.
由-1≤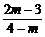 ≤1
≤1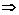 -1≤m≤
-1≤m≤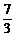 .
.
答案:D
1.(2004年上海,1)若tanα=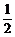 ,则tan(α+
,则tan(α+ )=____________.
)=____________.
解析:tan(α+ )=
)=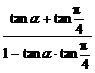 =
=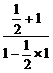 =3.
=3.
答案:3
5.△ABC中,若b=2a,B=A+60°,则A=_______.
解析:利用正弦定理,由b=2a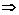 sinB=2sinA
sinB=2sinA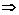 sin(A+60°)-2sinA=0
sin(A+60°)-2sinA=0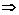
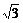 cosA-3sinA=0
cosA-3sinA=0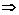 sin(30°-A)=0
sin(30°-A)=0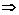 30°-A=0°(或180°)
30°-A=0°(或180°)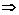 A=30°.
A=30°.
答案:30°
●典例剖析
[例1] 设cos(α-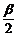 )=-
)=-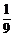 ,sin(
,sin(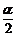 -β)=
-β)=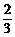 ,且
,且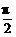 <α<π,0<β<
<α<π,0<β<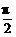 ,求cos(α+β).
,求cos(α+β).
剖析: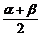 =(α-
=(α-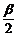 )-(
)-(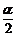 -β).
-β).
依上述角之间的关系便可求之.
解:∵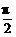 <α<π,0<β<
<α<π,0<β<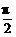 ,
,
∴ <α-
<α-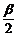 <π,-
<π,- <
<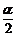 -β<
-β<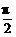 .
.
故由cos(α-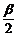 )=-
)=-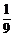 ,得sin(α-
,得sin(α-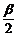 )=
)=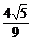 .
.
由sin(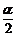 -β)=
-β)=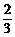 ,得cos(
,得cos(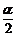 -β)=
-β)=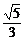 .
.
∴cos(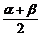 )=cos[(α-
)=cos[(α-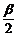 )-(
)-(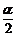 -β)]=…=
-β)]=…=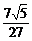 .
.
∴cos(α+β)=2cos2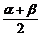 -1=…=-
-1=…=-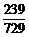 .
.
评述:在已知角的某一三角函数值而求另外一些角的三角函数值时,首先要分析已知和要求的角之间的关系,再分析函数名之间的关系.其中变角是常见的三角变换.
[例2] (2000年春季京、皖)在△ABC中,角A、B、C对边分别为a、b、c.
证明: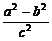 =
=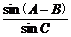 .
.
剖析:由于所证结论是三角形的边、角关系,很自然地使我们联想到正弦定理、余弦定理.
证明:由余弦定理a2=b2+c2-2bccosA,
b2=a2+c2-2accosB,
∴a2-b2=b2-a2-2bccosA+2accosB,
整理得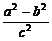 =
= .
.
依正弦定理有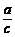 =
= ,
,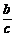 =
=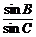 ,
,
∴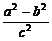 =
=
=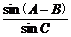 .
.
评述:在解三角形中的问题时,首先应想到正余弦定理,另外还有A+B+C=π,a+b>c,a>b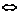 A>B
A>B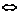 sinA>sinB等.
sinA>sinB等.
[例3] 已知α、β、γ∈(0,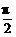 ),sinα+sinγ=sinβ,cosβ+cosγ=cosα,求β-α的值.
),sinα+sinγ=sinβ,cosβ+cosγ=cosα,求β-α的值.
剖析:由已知首先消去γ是解题关键.
解:由已知,得sinγ=sinβ-sinα,cosγ=cosα-cosβ.
平方相加得
(sinβ-sinα)2+(cosα-cosβ)2=1.
∴-2cos(β-α)=-1.∴cos(β-α)=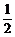 .
.
∴β-α=± .
.
∵sinγ=sinβ-sinα>0,∴β>α.∴β-α= .
.
评述:本题极易求出β-α=± ,如不注意隐含条件sinγ>0,则产生增根.因此求值问题要注意分析隐含条件.
,如不注意隐含条件sinγ>0,则产生增根.因此求值问题要注意分析隐含条件.
●闯关训练
夯实基础
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com