1.一个正方体内有一个内切球面，作正方体的对角面，所得截面图形是

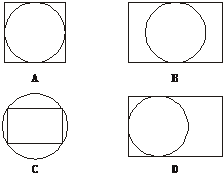
答案：B

2.正多面体有且只有5种.分别是正四面体、正六面体、正八面体、正十二面体、正二十面体.

●点击双基

1.每个面都是有相同边数的正多边形，每个顶点为端点都有相同棱数的凸多面体，叫做正多面体.

9.11　 多面体与正多面体

●知识梳理

4.仍以棱柱、棱锥为载体，训练计算能力.想象能力和逻辑推理能力.

拓展题例

[例1] 斜三棱柱的一个侧面的面积为S，这个侧面与它所对的棱的距离为d，那么这个三棱柱的体积为_____________.

解析：将该斜三棱柱补成一个四棱柱，该四棱柱的底面积为S，高为d，故四棱柱的体积为Sd，

∴V_斜三棱柱=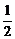dS.

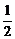答案： dS

[例2] 已知三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直且长度分别为a、b、c，设O为S在底面ABC上的射影.求证：

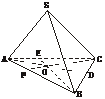
(1)O为△ABC的垂心；(2)O在△ABC内；(3)设SO=h，则 + +=.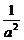

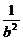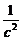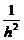证明：(1)∵SA⊥SB，SA⊥SC，

∴SA⊥平面SBC，BC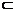平面SBC.∴SA⊥BC.

而AD是SA在平面ABC上的射影，∴AD⊥BC.

同理可证AB⊥CF，AC⊥BE，故O为△ABC的垂心.

(2)证明△ABC为锐角三角形即可.不妨设a≥b≥c，则底面三角形ABC中，AB=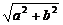为最大，从而∠ACB为最大角.

用余弦定理求得cos∠ACB=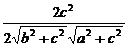>0，∴∠ACB为锐角，△ABC为锐角三角形.故O在△ABC内.

(3)SB·SC=BC·SD，

故SD=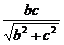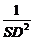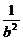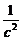，= +，又SA·SD=AD·SO，

∴===+= ++=.

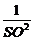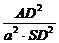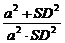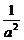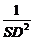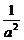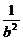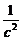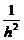3.在解答棱柱、棱锥的综合练习时，要善于联想，灵活运用柱、锥的性质和线面关系，善于揭示一类问题的共同特征，掌握基本方法，对于正棱柱、直棱柱问题借助空间坐标系或向量的运算或许更容易理解、掌握.

2.要使学生理解棱锥、正棱锥的意义，掌握棱锥、正棱锥的性质，会求其侧面积及体积.结合例题讲清求体积的常用方法.

1.使学生正确理解棱柱、直棱柱、正棱柱、平行六面体、长方体及正方体等有关概念，掌握棱柱的性质及长方体对角线性质，会求棱柱的侧面积及体积.

2.三棱锥的等(体)积变换是解决点到面的距离的常见方法之一，同时也是使计算简化的灵活手法；“割”“补”是解决体积问题的常用技巧.正棱锥的四个“特征”直角三角形，是将“空间问题”转化为“平面问题”的桥梁.

●教师下载中心

教学点睛

1.棱柱是第一章有关线面关系的载体，棱柱的计算证明问题常借助于前面的内容来解决.因此要牢固掌握线面间的位置关系的性质、判定.