
1.二元一次不等式表示平面区域
在平面直角坐标系中,已知直线Ax+By+C=0,坐标平面内的点P(x0,y0).
B>0时,①Ax0+By0+C>0,则点P(x0,y0)在直线的上方;②Ax0+By0+C<0,则点P(x0,y0)在直线的下方.
对于任意的二元一次不等式Ax+By+C>0(或<0),无论B为正值还是负值,我们都可以把y项的系数变形为正数.
当B>0时,①Ax+By+C>0表示直线Ax+By+C=0上方的区域;②Ax+By+C<0表示直线Ax+By+C=0下方的区域.
7.4 简单的线性规划
●知识梳理
3.对称问题除了用中点坐标公式及斜率关系来求以外,还可以用求轨迹的思想--代入法来求解.
拓展题例
[例1] 已知两点A(2,3)、B(4,1),直线l:x+2y-2=0,在直线l上求一点P.
(1)使|PA|+|PB|最小;
(2)使|PA|-|PB|最大.
解:(1)可判断A、B在直线l的同侧,设A点关于l的对称点A1的坐标为(x1,y1).
|
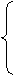
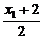 +2·
+2·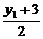 -2=0,
-2=0,
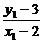 ·(-
·(-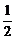 )=-1.
)=-1.
|
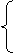 x1=-
x1=-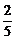 ,
,
y1=-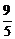 .
.
由两点式求得直线A1B的方程为y=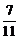 (x-4)+1,直线A1B与l的交点可求得为P(
(x-4)+1,直线A1B与l的交点可求得为P(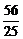 ,-
,-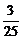 ).
).
由平面几何知识可知|PA|+|PB|最小.
(2)由两点式求得直线AB的方程为y-1=-(x-4),即x+y-5=0.
直线AB与l的交点可求得为P(8,-3),它使|PA|-|PB|最大.
[例2] 直线l经过点(1,1),若抛物线y2=x上存在两点关于直线l对称,求直线l斜率的取值范围.
解法一:设直线l的方程为y-1=k(x-1),弦的两个端点分别是A(x1,y1)、B(x2,y2),代入抛物线方程并作差得(y1+y2)(y1-y2)=x1-x2.
∵kAB=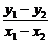 =-
=-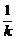 ,
,
∴y1+y2=-k.注意到AB的中点在直线l:y-1=k(x-1)上,∴x1+x2=1-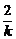 .
.
∴y12+y22=x1+x2=1-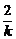 .
.
由y12+y22>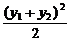 ,得1-
,得1-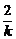 >
>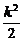
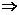
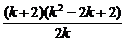 <0
<0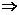 -2<k<0.
-2<k<0.
|
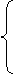 解法二:设抛物线上关于直线l:y-1=k(x-1)对称的两点为(y12,y1)、(y22,y2),
解法二:设抛物线上关于直线l:y-1=k(x-1)对称的两点为(y12,y1)、(y22,y2), 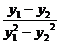 =-
=-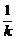
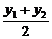 -1=k(
-1=k(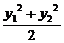 -1)
-1)
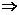
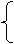 y1+y2=-k,
y1+y2=-k,
y1y2=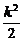 +
+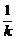 -
-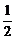 ,
,
∴y1、y2是方程y2+ky+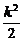 +
+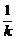 -
-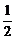 =0的两根.
=0的两根.
由Δ=k2-4(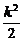 +
+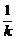 -
-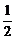 )>0
)>0
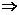
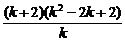 <0
<0
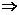 -2<k<0.
-2<k<0.
2.许多问题都隐含着对称性,要注意挖掘、充分利用对称变换来解决,如角平分线、线段中垂线、光线反射等.
1.对称问题的核心是点关于点的中心对称和点关于直线的轴对称,要充分利用转化的思想将问题转化为这两类对称中的一种加以处理.
3.本章的内容是解析几何最基本的概念、公式和法则,这些内容的综合应用是高考中经常考查的内容.
●教师下载中心
教学点睛
2.解决最值问题最常用的方法是目标函数法和几何法.
1.对称问题分为点对称及轴对称.点对称仅用中点坐标公式即可解决,轴对称因对称点连线的中垂线就是对称轴,根据中点坐标公式及斜率的关系即可解决.特别是关于原点对称、坐标轴对称、直线x±y=0对称都要熟练掌握.
9.(2003年新课程,理10)已知长方形的四个顶点A(0,0)、B(2,0)、C(2,1)和D(0,1),一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2、P3和P4(入射角等于反射角).设P4的坐标为(x4,0).若1<x4<2,求tanθ的取值范围.
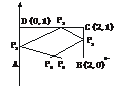
解:设P1B=x,∠P1P0B=θ,则CP1=1-x,
∠P1P2C、∠P3P2D、∠AP4P3均为θ,∴tanθ=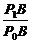 =x.
=x.
又tanθ=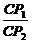 =
=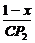 =x,
=x,
∴CP2=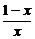 =
=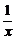 -1.
-1.
而tanθ=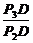 =
=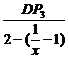 =
=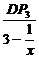 =x,
=x,
∴DP3=x(3-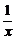 )=3x-1.
)=3x-1.
又tanθ=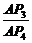 =
=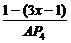 =
=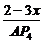 =x,
=x,
∴AP4=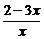 =
=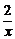 -3.
-3.
依题设1<AP4<2,即1<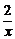 -3<2,
-3<2,
∴4<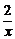 <5,
<5,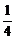 >
>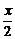 >
>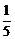 .
.
∴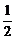 >tanθ>
>tanθ>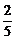 .
.
●思悟小结
8.(文)直线y=2x是△ABC中∠C的平分线所在的直线,若A、B坐标分别为A(-4,2)、B(3,1),求点C的坐标,并判断△ABC的形状.
解:由题意,点A关于直线y=2x的对称点A′在BC所在直线上,设A′点坐标为(x1,y1),则x1、y1满足
 =-
=-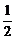 ,即x1=-2y1. ①
,即x1=-2y1. ①
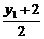 =2·
=2·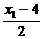 ,即2x1-y1-10=0. ②
,即2x1-y1-10=0. ②
解①②两式组成的方程组,得
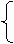 x1=4,
x1=4,
y1=-2.
∴BC所在直线方程为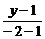 =
=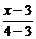 ,
,
即3x+y-10=0.
|
|
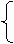 3x+y-10=0, x=2,
3x+y-10=0, x=2,
y=2x, y=4.
∴所求C点坐标为(2,4).
由题意|AB|2=50,|AC|2=40,|BC|2=10,
∴△ABC为直角三角形.
(理)若抛物线y=ax2-1上总存在关于直线x+y=0对称的两点,求实数a的取值范围.
解:设A(x1,y1)、B(x2,y2)是抛物线上关于直线x+y=0对称的两点,则AB的方程可设为y=x+b.
|
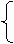 y=x+b,
y=x+b,
y=ax2-1,
得ax2-x-b-1=0,
可知Δ=1+4a(b+1)>0. ①
又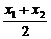 =
=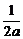 ,∴
,∴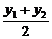 =-
=-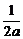 .
.
∴线段AB的中点M(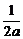 ,-
,-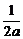 ).
).
∵M点在直线AB上,
∴-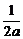 =
=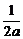 +b,即b=-
+b,即b=-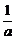 .
②
.
②
将②代入①得1+4a(1-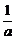 )>0.
)>0.
∴a>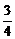 .
.
探究创新
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com