
5.(2002年全国)正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为1,侧棱长为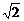 ,则这个棱柱的侧面对角线E1D与BC1所成的角是_____________.
,则这个棱柱的侧面对角线E1D与BC1所成的角是_____________.
解析:连结FE1、FD,则由正六棱柱相关性质可得FE1∥BC1,
在△EFD中,EF=ED=1,∠FED=120°,
∴FD=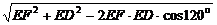 =
=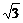 .
.
在△EFE1和△EE1D中,易得E1F=E1D=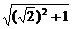 =
=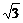 ,∴△E1FD是等边三角形,
,∴△E1FD是等边三角形,
∠FE1D=60°.而∠FE1D即为E1D与BC1所成的角.
答案:60°
说明:本题主要考查正六棱柱的性质及异面直线所成角的求法.
●典例剖析
[例1] 如下图,四面体ABCD中,E、G分别为BC、AB的中点,F在CD上,H在AD上,且有DF∶FC=2∶3,DH∶HA=2∶3.
求证:EF、GH、BD交于一点.
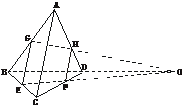
证明:连结GE、HF,
∵E、G分别为BC、AB的中点,
∴GE∥AC.
又∵DF∶FC=2∶3,DH∶HA=2∶3,
∴HF∥AC.∴GE∥HF.
故G、E、F、H四点共面.
又∵EF与GH不能平行,
∴EF与GH相交,设交点为O.
则O∈面ABD,O∈面BCD,而平面ABD∩平面BCD=BD.∴EF、GH、BD交于一点.
评述:证明线共点,常采用证两直线的交点在第三条直线上的方法,而第三条直线又往往是两平面的交线.
[例2] A是△BCD平面外的一点,E、F分别是BC、AD的中点,
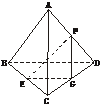
(1)求证:直线EF与BD是异面直线;
(2)若AC⊥BD,AC=BD,求EF与BD所成的角.
(1)证明:用反证法.设EF与BD不是异面直线,则EF与BD共面,从而DF与BE共面,即AD与BC共面,所以A、B、C、D在同一平面内,这与A是△BCD平面外的一点相矛盾.故直线EF与BD是异面直线.
(2)解:取CD的中点G,连结EG、FG,则EG∥BD,所以相交直线EF与EG所成的锐角或直角即为异面直线EF与BD所成的角.在Rt△EGF中,求得∠FEG=45°,即异面直线EF与BD所成的角为45°.
特别提示
①证明两条直线是异面直线常用反证法;②求两条异面直线所成的角,首先要判断两条异面直线是否垂直,若垂直,则它们所成的角为90°;若不垂直,则利用平移法求角,一般的步骤是“作(找)-证-算”.注意,异面直线所成角的范围是(0,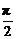 ].
].
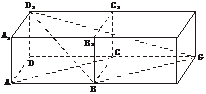
[例3] 长方体ABCD-A1B1C1D1中,已知AB=a,BC=b,AA1=c,且a>b,求:
(1)下列异面直线之间的距离:AB与CC1;AB与A1C1;AB与B1C.
(2)异面直线D1B与AC所成角的余弦值.
(1)解:BC为异面直线AB与CC1的公垂线段,故AB与CC1的距离为b.
AA1为异面直线AB与A1C1的公垂线段,故AB与A1C1的距离为c.过B作BE⊥B1C,垂足为E,则BE为异面直线AB与B1C的公垂线,BE=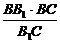 =
=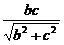 ,即AB与B1C的距离为
,即AB与B1C的距离为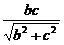 .
.
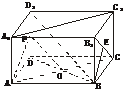
(2)解法一:连结BD交AC于点O,取DD1的中点F,连结OF、AF,则OF∥D1B,∴∠AOF就是异面直线D1B与AC所成的角.
∵AO=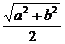 ,OF=
,OF=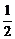 BD1=
BD1=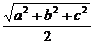 ,AF=
,AF=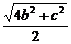 ,
,
∴在△AOF中,cos∠AOF=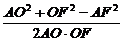 =
=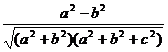 .
.
解法二:如下图,在原长方体的右侧补上一个同样的长方体,连结BG、D1G,则AC∥BG,∴∠D1BG(或其补角)为D1B与AC所成的角.
BD1=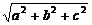 ,BG=
,BG=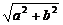 ,D1G=
,D1G=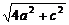 ,
,
在△D1BG中,cos∠D1BG=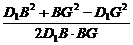 =-
=-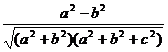 ,故所求的余弦值为
,故所求的余弦值为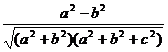 .
.
深化拓展
利用中位线平移和利用补形平移是处理长方体中异面直线所成角的重要方法.
●闯关训练
夯实基础
4.如下图,正方体ABCD-A1B1C1D1的棱长为a, 那么
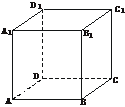
(1)哪些棱所在直线与直线BA1成异面直线?______________________.
(2)直线BA1与CC1所成角的大小为________.
(3)直线BA1与B1C所成角的大小为________.
(4)异面直线BC与AA1的距离为________.
(5)异面直线BA1与CC1的距离是________.
答案:(1)D1C1、D1D、C1C、C1B1、DC、AD
(2)45° (3)60° (4)a (5)a
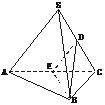
3.(2004年北京朝阳区模拟题)如下图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是
A.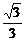 B.
B.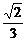 C.
C.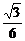 D.
D.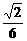
解析:取AC的中点E,连结DE、BE,则DE∥SA,∴∠BDE就是BD与SA所成的角.设SA=a,则BD=BE=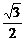 a,DE=
a,DE=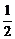 a,cos∠BDE=
a,cos∠BDE=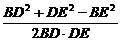 =
= 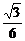 .
.
答案:C
2.如下图,直线a、b相交于点O且a、b成60°角,过点O与a、b都成60°角的直线有
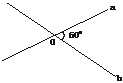
A.1条 B.2条 C.3条 D.4条
解析:在a、b所确定的平面内有一条,平面外有两条.
答案:C
1.若a,b是异面直线,则只需具备的条件是
A.a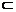 平面α,b
平面α,b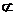 平面α,a与b不平行
平面α,a与b不平行
B.a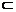 平面α,b
平面α,b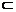 平面β,α∩β=l,a与b无公共点
平面β,α∩β=l,a与b无公共点
C.a∥直线c,b∩c=A,b与a不相交
D.a⊥平面α,b 是α的一条斜线
答案:C
4.两条异面直线所成的角及距离,求作异面直线所成的角时,往往取题中的特殊点.
●点击双基
3.空间两条直线的位置关系有且只有三种,即平行、相交及异面.
2.公理4及等角定理.
1.平面的基本性质,即三个公理及推论.
9.1 平面、空间两条直线
●知识梳理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com