
2.转化法则是把点面距离转化为线面距离,或把线面距离转化为面面距离,再转化为点面距离.
1.直接法是直接作出垂线,再通过解三角形求出距离.
9.(2003年南京质量检测题)如图,正三棱柱ABC-A1B1C1的底面边长为a,点M在边BC上,△AMC1是以点M为直角顶点的等腰直角三角形.
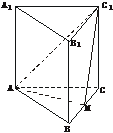
(1)求证:点M为边BC的中点;
(2)求点C到平面AMC1的距离.
(1)证明:∵△AMC1为以点M为直角顶点的等腰直角三角形,
∴AM⊥C1M且AM=C1M.
∵ABC-A1B1C1是正三棱柱,
∴CC1⊥底面ABC.
∴C1M在底面内的射影为CM,AM⊥CM.
∵底面ABC为边长为a的正三角形,
∴点M为BC边的中点.
(2)解:过点C作CH⊥MC1,
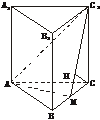
由(1)知AM⊥C1M且AM⊥CM,
∴AM⊥平面C1CM.
∵CH⊥AM,∴CH⊥平面C1AM,
由(1)知,AM=C1M=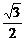 a,CM=
a,CM=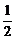 a且CC1⊥BC.∴CC1=
a且CC1⊥BC.∴CC1=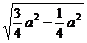 =
= 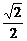 a.
a.
∴CH=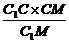 =
=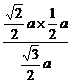 =
=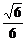 a.
a.
∴点C到平面AMC1的距离为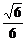 a.
a.
●思悟小结
求空间距离的方法可分为直接法、转化法、向量法.
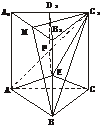
8.(2003年东城区一模题)如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
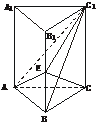
(1)求直线C1B与平面A1ABB1所成角的正弦值;
(2)求证:平面AEC1⊥平面ACC1A1;
(3)求点C1到平面AEC的距离.
(1)解:取A1B1中点M,连结C1M,BM.
∵三棱柱ABC-A1B1C1是正三棱柱,
∴C1M⊥A1B1,C1M⊥BB1.
∴C1M⊥平面A1ABB1.
∴∠C1BM为直线C1B与平面A1ABB1所成的角.
在Rt△BMC1中,C1M=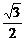 a,BC1=
a,BC1=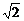 a,
a,
∴sin∠C1BM=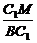 =
=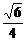 .
.
(2)证明:取A1C1的中点D1,AC1的中点F,连结B1D1、EF、D1F.则有D1F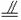
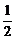 AA1,B1E
AA1,B1E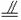
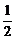 AA1.
AA1.
∴D1F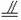 B1E.
B1E.
则四边形D1FEB1是平行四边形,
∴EF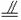 B1D1.
B1D1.
由于三棱柱ABC-A1B1C1是正三棱柱,
∴B1D1⊥A1C1.
又平面A1B1C1⊥平面ACC1A1于A1C1,且B1D1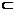 平面A1B1C1,∴B1D1⊥平面ACC1A1.
平面A1B1C1,∴B1D1⊥平面ACC1A1.
∴EF⊥平面ACC1A1.
∵EF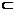 平面AEC1,则平面AEC1⊥平面ACC1A1.
平面AEC1,则平面AEC1⊥平面ACC1A1.
(3)由(2)知,EF⊥平面AC1,则EF是三棱锥E-ACC1的高.
由三棱柱各棱长都等于a,则EC=AE=EC1=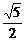 a,AC1=
a,AC1=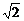 a.
a.
∴EF=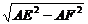 =
=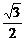 a.
a.
∵V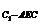 =V
=V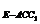 ,设三棱锥V
,设三棱锥V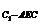 的高为h,则h为点C1到平面AEC的距离.
的高为h,则h为点C1到平面AEC的距离.
则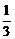 S
S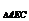 ·h=
·h=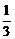 S
S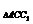 ·EF,
·EF,
即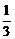 ×
×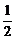 a2h=
a2h=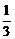 ×
×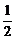 a2·
a2·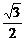 a.
a.
∴h=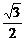 a,即点C1到平面AEC的距离是
a,即点C1到平面AEC的距离是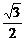 a.
a.
探究创新
7.已知直线l上有两定点A、B,线段AC⊥l,BD⊥l,AC=BD=a且AC与BD成120°角,求AB与CD间的距离.
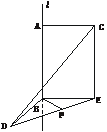
解法一:在面ABC内过B作BE⊥l于B,且BE=AC,则ABEC为矩形.
∴AB∥CE.
∴AB∥平面CDE.
则AB与CD的距离即为B到DE的距离.
过B作BF⊥DE于F,易求BF=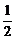 a.
a.
解法二:建系如图,
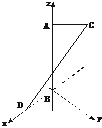
则A(0,0,b),C(-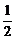 a,
a,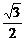 a,a),D(a,0,0),
a,a),D(a,0,0),
设AB与CD的公垂线的一个方向向量n=(x,y,z),
利用n·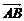 =0,n·
=0,n·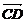 =0,
=0,
求出n,则d=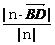 =
=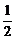 a.
a.
6.已知正方体ABCD-A1B1C1D1的边长为a,E、F分别是棱A1B1、CD的中点.
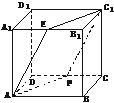
(1)证明:截面C1EAF⊥平面ABC1.
(2)求点B到截面C1EAF的距离.
(1)证明:连结EF、AC1和BC1,易知四边形EB1CF是平行四边形,从而EF∥B1C,直线B1C⊥BC1且B1C⊥AB,则直线B1C⊥平面ABC1,得EF⊥平面ABC1.而EF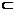 平面C1EAF,得平面C1EAF⊥平面ABC1.
平面C1EAF,得平面C1EAF⊥平面ABC1.
(2)解:在平面ABC1内,过B作BH,使BH⊥AC1,H为垂足,则BH的长就是点B到平面C1EAF的距离,在直角三角形中,BH=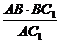 =
=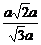 =
=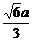 .
.
培养能力
5.ABCD是正方形,边长为7 cm,MN∥AB且交BC于点M,交DA于点N,若AN=3 cm,沿MN把正方形折成如图所示的二面角A-MN-D,大小为60°,求图中异面直线MN与BD间的距离.
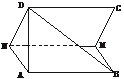
解:由题意易证MN∥平面ABD,MN与BD的距离可转化为点N到平面ABD的距离,作NE⊥AD,易证NE⊥平面ABD,故可求NE=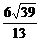 .
.
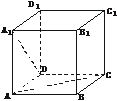
4.(B)已知正方体ABCD-A1B1C1D1的棱长为1,则直线DA1与AC间的距离为__________.
解析:设n=λ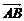 +μ
+μ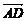 +
+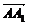 是A1D和AC的公垂线段上的向量,则n·
是A1D和AC的公垂线段上的向量,则n·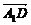 =(λ
=(λ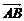 +μ
+μ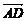 +
+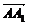 )·(
)·(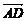 -
-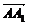 )=μ-1=0,∴μ=1.
)=μ-1=0,∴μ=1.
又n·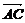 =(λ
=(λ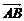 +μ
+μ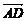 +
+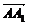 )·(
)·(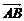 +
+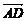 )=λ+μ=0,∴λ=-1.
)=λ+μ=0,∴λ=-1.
∴n=-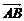 +
+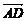 +
+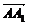 .故所求距离为
.故所求距离为
d=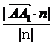 =|AA1·
=|AA1·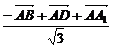 |=
|=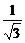 =
= 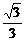 .
.
答案: 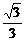
3.已知l1、l2是两条异面直线,α、β、γ是三个互相平行的平面,l1、l2分别交α、β、γ于A、B、C和D、E、F,AB=4,BC=12,DF=10,又l1与α成30°角,则β与γ的距离是__________;DE=__________.
解析:由直线与平面所成角的定义及平行平面距离定义易得β与γ间距离为6.由面面平行的性质定理可得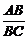 =
=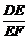 ,∴
,∴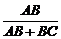 =
=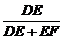 ,即
,即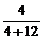 =
=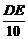 .∴DE=2.5.
.∴DE=2.5.
答案:6 2.5
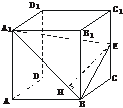
2.正方体ABCD-A1B1C1D1的棱长为a,E是CC1的中点,则E到A1B的距离是
A. 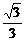 a B.
a B.
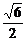 a C.
a C.
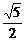 a D.
a D.
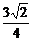 a
a
解析:连结A1E、BE,过E作EH⊥A1B于H,
在△A1BE中易求EH=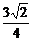 a.
a.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com