
1.两个平面平行的判定定理:如果一个平面的两条相交直线都与另一个平面平行,那么这两个平面平行.
9.4 两个平面平行
●知识梳理
2.通过例题的讲解给学生总结归纳证明线面垂直的常见方法:(1)证直线与平面内的两条相交直线都垂直;(2)证与该线平行的直线与已知平面垂直;(3)借用面面垂直的性质定理;(4)同一法.
拓展题例
[例1] (2003年全国)下列五个正方体图形中,l是正方体的一条对角线,点M、N、P分别是其所在棱的中点,能得出l⊥平面MNP的图形的序号是_____________.
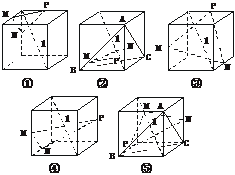
解析:对①,易用三垂线定理证明l⊥MN,l⊥PM,故l⊥平面MNP;对②,易知l⊥平面ABC,但点M、N位于该平面的两侧,故平面MNP不平行平面ABC,从而l不垂直平面MNP;同理,③也不垂直;对④,易证l⊥MN,l⊥MP,故④正确;对⑤,易知平面MNP∥平面ABC,而l⊥平面ABC,故⑤正确.
答案:①④⑤
[例2] (2004年春季上海)如下图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
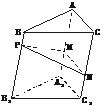
(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF·EFcos∠DFE.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
(1)证明:∵CC1∥BB1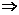 CC1⊥PM,CC1⊥PN,
CC1⊥PM,CC1⊥PN,
∴CC1⊥平面PMN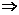 CC1⊥MN.
CC1⊥MN.
(2)解:在斜三棱柱ABC-A1B1C1中,有S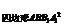 =S
=S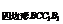 2+S
2+S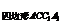 2-2S
2-2S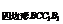 ·S
·S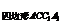 cosα,其中α为平面CC1B1B与平面CC1A1A所成的二面角.
cosα,其中α为平面CC1B1B与平面CC1A1A所成的二面角.
∵CC1⊥平面PMN,∴上述的二面角为∠MNP.
在△PMN中,PM2=PN2+MN2-2PN·MNcos∠MNP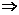 PM2CC12=PN2CC12+MN2CC12-
PM2CC12=PN2CC12+MN2CC12-
2(PN·CC1)·(MN·CC1)cos∠MNP.
由于S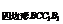 =PN·CC1,S
=PN·CC1,S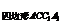 =MN·CC1,S
=MN·CC1,S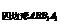 =PM·BB1,
=PM·BB1,
∴有S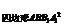 =S
=S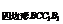 2+S
2+S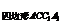 2-2S
2-2S ·S
·S cosα.
cosα.
1.使学生熟练掌握线面垂直的判定定理及性质定理.
3.运用三垂线定理及其逆定理的关键在于确定斜线在平面上的射影,而确定射影的关键又是“垂足”,如果“垂足”定了,那么“垂足”和“斜足”的连线就是斜线在平面上的射影.
●教师下载中心
教学点睛
2.注意线面垂直与线线垂直的关系和转化.
1.直线与平面垂直是直线与平面相交的一种特殊情况,应熟练掌握直线与平面垂直的定义、判定定理、性质定理,并能依据条件灵活运用.
9.正方形ABCD中,AB=2,E是AB边的中点,F是BC边上一点,将△AED及△DCF折起(如下图),使A、C点重合于A′点.
(1)证明:A′D⊥EF;
(2)当F为BC的中点时,求A′D与平面DEF所成的角;
(3)当BF=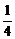 BC时,求三棱锥A′-EFD的体积.
BC时,求三棱锥A′-EFD的体积.
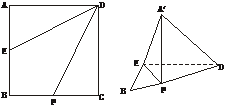
(1)证明:∵A′D⊥A′E,A′D⊥A′F,
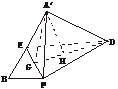
∴A′D⊥平面A′EF.∴A′D⊥EF.
(2)解:取EF的中点G,连结A′G、DG.
∵BE=BF=1,∠EBF=90°,∴EF=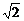 .
.
又∵A′E=A′F=1,
∴∠EA′F=90°,A′G⊥EF,得A′G=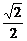 .
.
∵A′G⊥EF,A′D⊥EF,A′G∩A′D=A′,
∴EF⊥平面A′DG.
∴平面DEF⊥平面A′DG.
作A′H⊥DG于H,得A′H⊥平面DEF,
∴∠A′DG为A′D与平面DEF所成的角.
在Rt△A′DG中,A′G=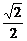 ,A′D=2,
,A′D=2,
∴∠A′DG=arctan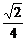 .
.
(3)解:∵A′D⊥平面A′EF,
∴A′D是三棱锥D-A′EF的高.
又由BE=1,BF=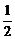 推出EF=
推出EF=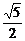 ,
,
可得S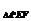 =
=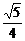 ,
,
VA′-EFD=VD-A′EF=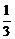 ·S
·S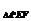 ·A′D=
·A′D=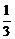 ·
·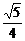 ·2=
·2=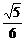 .
.
●思悟小结
8.在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,BC=a,又侧棱PA⊥底面ABCD.
(1)当a为何值时,BD⊥平面PAC?试证明你的结论.
(2)当a=4时,求证:BC边上存在一点M,使得PM⊥DM.
(3)若在BC边上至少存在一点M,使PM⊥DM,求a的取值范围.
分析:本题第(1)问是寻求BD⊥平面PAC的条件,即BD垂直平面PAC内两相交直线,易知BD⊥PA,问题归结为a为何值时,BD⊥AC,从而知ABCD为正方形.
(1)解:当a=2时,ABCD为正方形,则BD⊥AC.
又∵PA⊥底面ABCD,BD 平面ABCD,
平面ABCD,
∴BD⊥PA.∴BD⊥平面PAC.
故当a=2时,BD⊥平面PAC.
(2)证明:当a=4时,取BC边的中点M,AD边的中点N,连结AM、DM、MN.
∵ABMN和DCMN都是正方形,
∴∠AMD=∠AMN+∠DMN=45°+45°=90°,即DM⊥AM.又PA⊥底面ABCD,由三垂线定理得,PM⊥DM,故当a=4时,BC边的中点M使PM⊥DM.
(3)解:设M是BC边上符合题设的点M,
∵PA⊥底面ABCD,∴DM⊥AM.
因此,M点应是以AD为直径的圆和BC边的一个公共点,则AD≥2AB,即a≥4为所求.
评述:本题的解决中充分运用了平面几何的相关知识.因此,立体几何解题中,要注意有关的平面几何知识的运用.事实上,立体几何问题最终是在一个或几个平面中得以解决的.
探究创新
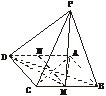
7.如下图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,
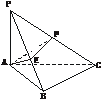
求证:(1)BC⊥平面PAB;
(2)AE⊥平面PBC;
(3)PC⊥平面AEF.
 证明:(1)PA⊥平面ABC
证明:(1)PA⊥平面ABC
|
AB⊥BC
PA∩AB=A
|
 (2)AE
(2)AE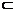 平面PAB,由(1)知AE⊥BC
平面PAB,由(1)知AE⊥BC
AE⊥PB
PB∩BC=B
|
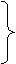 (3)PC
(3)PC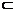 平面PBC,由(2)知PC⊥AE
平面PBC,由(2)知PC⊥AE
PC⊥AF
AE∩AF=A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com