1.本题用分析法直接去证可以吗?

2.由于高考试题不会出现单一的不等式的证明题，常常与函数、数列、三角、方程综合在一起，所以在教学中，不等式的证明除常用的三种方法外，还需介绍其他方法，如函数的单调性法、判别式法、换元法(特别是三角换元)、放缩法以及数学归纳法等.

拓展题例

[例1] 已知a、b为正数，求证：

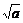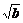(1)若+1＞，则对于任何大于1的正数x，恒有ax+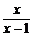＞b成立；

(2)若对于任何大于1的正数x，恒有ax+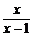＞b成立，则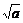+1＞.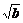

分析：对带条件的不等式的证明，条件的利用常有两种方法：①证明过程中代入条件；②由条件变形得出要证的不等式.

证明：(1)ax+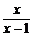=a(x－1)+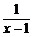+1+a≥2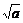+1+a=(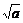+1)².

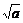∵+1＞b(b＞0)，

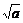∴(+1)²＞b².

(2)∵ax+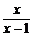＞b对于大于1的实数x恒成立，即x＞1时，［ax+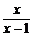］_min＞b，

而ax+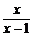=a(x－1)+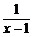+1+a≥2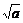+1+a=(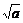+1)²，

当且仅当a(x－1)=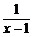，即x=1+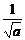＞1时取等号.

故［ax+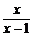］_min=(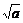+1)².

则(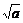+1)²＞b，即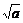+1＞b.

评述：条件如何利用取决于要证明的不等式两端的差异如何消除.

[例2] 求证：≤+.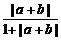

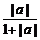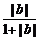剖析：|a+b|≤|a|+|b|，故可先研究f(x)=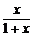(x≥0)的单调性.

证明：令f(x)=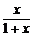(x≥0)，易证f(x)在［0，+∞)上单调递增.

|a+b|≤|a|+|b|，

∴f(|a+b|)≤f(|a|+|b|)，

即≤=≤.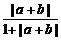

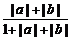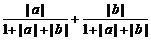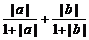思考讨论

1.在证明不等式的过程中，分析法和综合法是不能分离的，如果使用综合法证明不等式难以入手时，常用分析法探索证题途径，之后用综合法的形式写出它的证明过程，以适应学生习惯的思维规律.有时问题证明难度较大，常使用分析综合法，实现两头往中间靠以达到证题目的.

4.构造函数利用单调性证不等式或构造方程利用“Δ≥0”证不等式，充分体现相关知识间的联系.

●教师下载中心

教学点睛

3.探求不等式的证法一般用分析法，叙述证明过程用综合法较简，两法结合在证明不等式中经常遇到.

2.分析法就是“执果索因”，从所证不等式出发，不断用充分条件替换前面的不等式，直至找到成立的不等式.

1.综合法就是“由因导果”，从已知不等式出发，不断用必要条件替换前面的不等式，直至推出要证的结论.

8.已知a、b、c、d∈R，且a+b=c+d=1，ac+bd＞1.

求证：a、b、c、d中至少有一个是负数.

证明：假设a、b、c、d都是非负数，

∵a+b=c+d=1，∴(a+b)(c+d)=1.

∴ac+bd+bc+ad=1≥ac+bd.

这与ac+bd＞1矛盾.

所以假设不成立，即a、b、c、d中至少有一个负数.

●思悟小结

7.设a、b、c均为实数，求证：++≥++.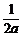

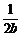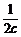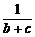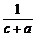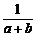证明：∵a、b、c均为实数，

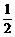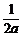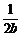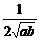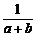∴(+)≥≥，当a=b时等号成立；

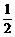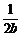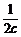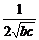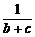(+)≥≥，当b=c时等号成立；

(+)≥≥．

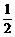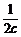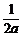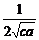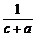三个不等式相加即得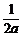++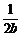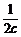≥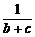++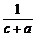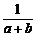，当且仅当a=b=c时等号成立.

探究创新

6.已知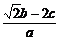=1，求证：方程ax²+bx+c=0有实数根.

证明：由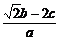=1，∴b=.

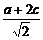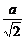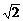∴b²=(+c)²=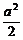+2ac+2c²=4ac+(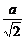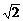－c)²≥4ac.

∴方程ax²+bx+c=0有实数根.