
1.应用不等式解决数学问题时,关键在于要善于把等量关系转化为不等量关系,以及不等关系的转化等,把问题转化为不等式的问题求解.
5.化归思想在本节占有重要位置,等式和不等式之间的转化、不等式和不等式之间的转化、函数与不等式之间的转化等,对于这些转化,一定要注意条件.
●教师下载中心
教学点睛
4.利用重要不等式求最值时,要注意条件:一正、二定、三相等,即在x+y≥2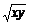 中,x和y要大于零,要有定积或定和出现;同时要求“等号”成立.
中,x和y要大于零,要有定积或定和出现;同时要求“等号”成立.
3.解不等式应用问题的三个步骤:
(1)审题,必要时画出示意图;
(2)建立不等式模型,即根据题意找出常量与变量的不等关系;
(3)利用不等式的有关知识解题,即将数学模型转化为数学符号或图形符号.
2.建立不等式的主要途径有:(1)利用问题的几何意义;(2)利用判别式;(3)利用函数的有界性;(4)利用函数的单调性.
1.不等式的应用大致可分为两类:一类是建立不等式求参数的取值范围或解决一些实际应用问题;另一类是建立函数关系,利用均值不等式求最值问题.
9.有点难度哟!
已知a>b>0,求a2+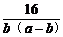 的最小值.
的最小值.
解:∵b(a-b)≤(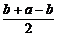 )2=
)2=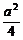 ,
,
∴a2+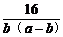 ≥a2+
≥a2+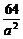 ≥16.
≥16.
当且仅当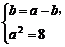 ,即
,即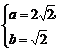 时取等号.
时取等号.
深化拓展
a>b>0,求b(a-b)·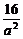 的最大值.
的最大值.
提示:b(a-b)≤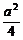 .
.
答案:4
●思悟小结
8.已知函数f(x)=x2+bx+c(b、c∈R)且当x≤1时,f(x)≥0,当1≤x≤3时,f(x)≤0恒成立.
(1)求b、c之间的关系式;
(2)当c≥3时,是否存在实数m使得g(x)=f(x)-m2x在区间(0,+∞)上是单调函数?若存在,求出m的取值范围;若不存在,请说明理由.
解:(1)由已知f(1)≥0与f(1)≤0同时成立,则必有f(1)=0,故b+c+1=0.
(2)假设存在实数m,使满足题设的g(x)存在.
∵g(x)=f(x)-m2x=x2+(b-m2)x+c开口向上,且在[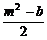 ,+∞)上单调递增,
,+∞)上单调递增,
∴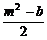 ≤0.∴b≥m2≥0.
≤0.∴b≥m2≥0.
∵c≥3,∴b=-(c+1)≤-4.
这与上式矛盾,从而能满足题设的实数m不存在.
探究创新
7.(2003年全国)已知c>0,设P:函数y=cx在R上单调递减,Q:不等式x+|x-2c|>1的解集为R.如果P和Q有且仅有一个正确,求c的取值范围.
解:函数y=cx在R上单调递减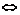 0<c<1.
0<c<1.
不等式x+|x-2c|>1的解集为R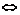 函数y=x+|x-2c|在R上恒大于1.
函数y=x+|x-2c|在R上恒大于1.
∵x+|x-2c|=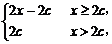
∴函数y=x+|x-2c|在R上的最小值为2c.
∴不等式x+|x-2c|>1的解集为R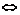 2c>1
2c>1 c>
c>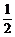 .
.
如果P正确,且Q不正确,则0<c≤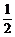 .
.
如果P不正确,且Q正确,则c≥1.
∴c的取值范围为(0,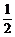 ]∪[1,+∞).
]∪[1,+∞).
6.(2004年春季上海)已知实数p满足不等式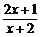 <0,试判断方程z2-2z+5-p2=0有无实根,并给出证明.
<0,试判断方程z2-2z+5-p2=0有无实根,并给出证明.
解:由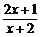 <0,解得-2<x<-
<0,解得-2<x<-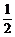 .
.
∴-2<p<-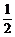 .
.
∴方程z2-2z+5-p2=0的判别式Δ=4(p2-4).
∵-2<p<-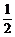 ,
,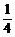 <p2<4,
<p2<4,
∴Δ<0.
由此得方程z2-2z+5-p2=0无实根.
培养能力
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com