
4.(2003年春季上海)若正三棱锥底面边长为4,体积为1,则侧面和底面所成二面角的大小等于_______.(结果用反三角函数值表示)
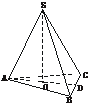
解析:取BC的中点D,连结SD、AD,则SD⊥BC,AD⊥BC.
∴∠SDA为侧面与底面所成二面角的平面角,设为α.在平面SAD中,作SO⊥AD与AD交于O,则SO为棱锥的高.
AO=2DO,∴OD=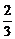
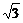 .
.
又VS-ABC=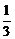 ·
·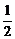 AB·BC·sin60°·h=1,
AB·BC·sin60°·h=1,
∴h=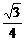 .∴tanα=
.∴tanα=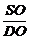 =
=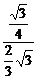 =
=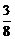 .
.
∴α=arctan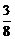 .
.
答案:arctan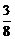
3.将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积为
A.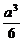 B.
B.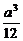 C.
C.
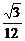 a3 D.
a3 D.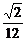 a3
a3
答案:D
2.如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在
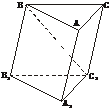
A.直线AB上 B.直线BC上 C.直线AC上 D.△ABC内部
解析:由AC⊥AB,AC⊥BC1,知AC⊥面ABC1,从而面ABC1⊥面ABC,因此,C1在底面ABC上的射影H必在两面的交线AB上.
答案:A
1.设M={正四棱柱},N={直四棱柱},P={长方体},Q={直平行六面体},则四个集合的关系为
A.M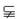 P
P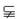 N
N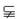 Q B.M
Q B.M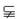 P
P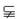 Q
Q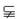 N C.P
N C.P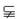 M
M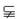 N
N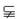 Q D.P
Q D.P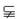 M
M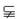 Q
Q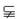 N
N
解析:理清各概念的内涵及包含关系.
答案:B
4.棱锥中与底面平行的截面与底面平行,并且它们面积的比等于对应高的平方比.
在正棱锥中,侧棱、高及侧棱在底面上的射影构成直角三角形;斜高、高及斜高在底面上的射影构成直角三角形.
●点击双基
3.一个面是多边形,其余各面是有一个公共顶点的三角形的多面体叫做棱锥.底面是正多边形并且顶点在底面上的射影是正多边形的中心的棱锥叫做正棱锥.
2.棱柱的各侧棱相等,各侧面都是平行四边形;长方体的对角线的平方等于由一个顶点出发的三条棱的平方和.
1.有两个面互相平行,其余各面的公共边互相平行的多面体叫做棱柱.侧棱与底面垂直的棱柱叫做直棱柱.底面是正多边形的直棱柱叫正棱柱.
9.10 棱柱与棱锥
●知识梳理
2.证明三点均在两个平面的交线上,可以推证三点共线;求异面直线所成的角,一般先取一个特殊点作它们的平行线,作出所求的角或其补角,再解三角形.
●教师下载中心
教学点睛
首先要使学生掌握本节的重点内容:平面的基本性质、异面直线的定义及判断、异面直线所成的角,其次结合例题讲清求异面直线所成的角的方法步骤.
拓展题例
[例1] 设异面直线a与b所成的角为50°,O为空间一定点,试讨论,过点O与a、b所成的角都是θ(0°≤θ≤90°)的直线l有且仅有几条?
解:过点O作a1∥a,b1∥b,则相交直线a1、b1确定一平面α.a1与b1夹角为50°或130°,设直线OA与a1、b1均为θ角,作AB⊥面α于点B,BC⊥a1于点C,BD⊥b1于点D,记∠AOB=θ1,∠BOC=θ2(θ2=25°或65°),则有cosθ=cosθ1·cosθ2.因为0°≤θ1≤90°,所以
0≤cosθ≤cosθ2.
当θ2=25°时,由0≤cosθ≤cos25°,得25°≤θ≤90°;
当θ2=65°时,由0≤cosθ≤cos65°,得65°≤θ≤90°.
故当θ<25°时,直线l不存在;当θ=25°时,直线l有且仅有1条;
当25°<θ<65°时,直线l有且仅有2条;
当θ=65°时,直线l有且仅有3条;
当65°<θ<90°时,直线l有且仅有4条;
当θ=90°时,直线l有且仅有1条.
说明:异面直线所成的角就是选点、平移后的平面角.上述解答首先将问题转化为:求过点O与a1、b1均成θ角的直线的条数,进而通过讨论θ的范围去确定直线l的条数.
[例2] 已知空间四边形ABCD,E、H分别是AB、AD的中点,F、G分别是边BC、DC的三等分点(如下图),求证:
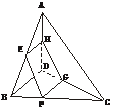
(1)对角线AC、BD是异面直线;
(2)直线EF和HG必交于一点,且交点在AC上.
证明:(1)假设对角线AC、BD在同一平面α内,则A、B、C、D都在平面α内,这与ABCD是空间四边形矛盾,∴AC、BD是异面直线.
(2)∵E、H分别是AB、AD的中点, ∴EH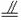
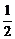 BD.
BD.
又F、G分别是BC、DC的三等分点,
∴FG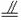
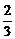 BD.∴EH∥FG,且EH<FG.
BD.∴EH∥FG,且EH<FG.
∴FE与GH相交.
设交点为O,又O在GH上,GH在平面ADC内,∴O在平面ADC内.
同理,O在平面ABC内.
从而O在平面ADC与平面ABC的交线AC上.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com