
5.化简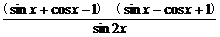 .
.
解:原式=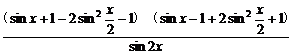
=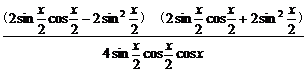
=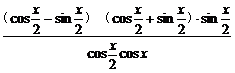
=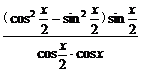 =
=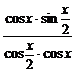 =tan
=tan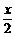 .
.
4.若tanx=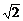 ,则
,则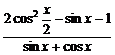 =_______.
=_______.
解析:原式=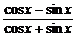 =
=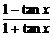 =
=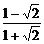 =
=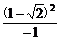 =2
=2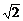 -3.
-3.
答案:2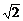 -3
-3
3.若8cos(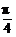 +α)cos(
+α)cos(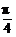 -α)=1,则sin4α+cos4α=_______.
-α)=1,则sin4α+cos4α=_______.
解析:由已知得8sin(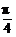 -α)cos(
-α)cos(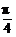 -α)=1,
-α)=1,
∴4sin( -2α)=1.∴cos2α=
-2α)=1.∴cos2α=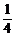 .
.
sin4α+cos4α=(sin2α+cos2α)2-2sin2αcos2α=1-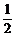 sin22α=1-
sin22α=1-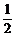 (1-cos22α)
(1-cos22α)
=1-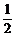 (1-
(1-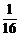 )=1-
)=1-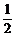 ×
×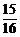 =
=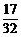 .
.
答案: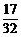
2.(2005年春季上海,14)在△ABC中,若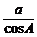 =
=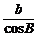 =
=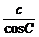 ,则△ABC是
,则△ABC是
A.直角三角形 B.等边三角形
C.钝角三角形 D.等腰直角三角形
解析:由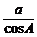 =
=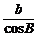 ,得
,得 =
=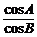 .
.
又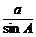 =
=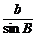 ,∴
,∴ =
=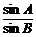 .
.
∴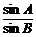 =
=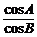 .∴sinAcosB=cosAsinB,
.∴sinAcosB=cosAsinB,
sin(A-B)=0,A=B.同理B=C.
∴△ABC是等边三角形.
答案:B
1.已知f(x)=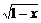 ,当θ∈(
,当θ∈(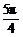 ,
, )时,f(sin2θ)-f(-sin2θ)可化简为
)时,f(sin2θ)-f(-sin2θ)可化简为
A.2sinθ B.-2cosθ C.-2sinθ D.2cosθ
解析:f(sin2θ)-f(-sin2θ)=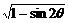 -
-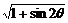 =|sinθ-cosθ|-|sinθ+
=|sinθ-cosθ|-|sinθ+
cosθ|.
∵θ∈(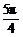 ,
, ),
),
∴-1<sinθ<-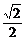 <cosθ<0.
<cosθ<0.
∴cosθ-sinθ>0,cosθ+sinθ<0.
∴原式=cosθ-sinθ+cosθ+sinθ=2cosθ.
答案:D
5.(2005年春季北京,11)已知sin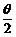 +cos
+cos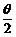 =
=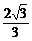 ,那么sinθ的值为____________,cos2θ的值为____________.
,那么sinθ的值为____________,cos2θ的值为____________.
解析:由sin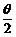 +cos
+cos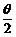 =
=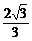 ,得
,得
1+sinθ=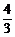 ,sinθ=
,sinθ=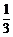 ,
,
cos2θ=1-2sin2θ=1-2·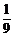 =
=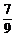 .
.
答案: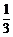
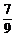
●典例剖析
[例1] 试求函数y=sinx+cosx+2sinxcosx+2的最大值和最小值,若x∈[0, ]呢?
]呢?
剖析:注意sinx+cosx与sinx·cosx之间的关系,进行换元可将原函数转化成一元二次函数来解.
解:令t=sinx+cosx=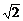 sin(x+
sin(x+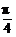 )∈[-
)∈[-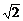 ,
,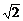 ],则y=t2+t+1∈[
],则y=t2+t+1∈[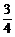 ,3+
,3+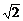 ],即最大值为3+
],即最大值为3+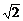 ,最小值为
,最小值为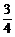 .当x∈[0,
.当x∈[0, ]时,则t∈[1,
]时,则t∈[1,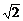 ],此时y的最大值是3+
],此时y的最大值是3+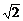 ,而最小值是3.
,而最小值是3.
评述:此题考查的是换元法,转化思想,在换元时要注意变量的取值范围.
[例2] 已知sin(x-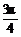 )cos(x-
)cos(x-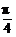 )=-
)=-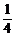 ,求cos4x的值.
,求cos4x的值.
剖析:4x为2x的二倍角,2x为x的二倍角.
解:由已知得sin(x- -
-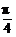 )cos(x-
)cos(x-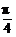 )=-
)=-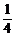 ,
,
∴cos2(x-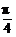 )=
)=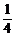 .
.
∴sin2x=cos( -2x)=2cos2(
-2x)=2cos2(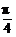 -x)-1=-
-x)-1=-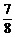 .
.
∴cos4x=1-2sin22x=1-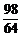 =-
=-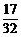 .
.
[例3] 已知α为第二象限角,cos +sin
+sin =-
=-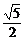 ,求sin
,求sin -cos
-cos 和sin2α+cos2α的值.
和sin2α+cos2α的值.
解:由cos +sin
+sin =-
=-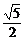 平方得
平方得
1+2sin cos
cos =
=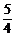 ,
,
即sinα=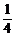 ,cosα=-
,cosα=-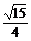 .
.
此时kπ+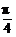 <
< <kπ+
<kπ+ .
.
∵cos +sin
+sin =-
=-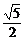 <0,
<0,
sin cos
cos =
=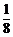 >0,
>0,
∴cos <0,sin
<0,sin <0.
<0.
∴ 为第三象限角.
为第三象限角.
∴2kπ+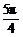 <
< <2kπ+
<2kπ+ ,k∈Z.
,k∈Z.
∴sin <cos
<cos ,
,
即sin -cos
-cos <0.
<0.
∴sin -cos
-cos =-
=-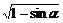 =-
=-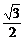 ,
,
sin2α+cos2α=2sinαcosα+1-2sin2α=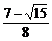 .
.
评述:由三角函数值判断 的范围是关键.
的范围是关键.
●闯关训练
夯实基础
4.(2005年春季上海,13)若cosα=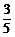 ,且α∈(0,
,且α∈(0, ),则tan
),则tan =____________.
=____________.
解析一:由cosα=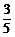 ,α∈(0,
,α∈(0, ),得sinα=
),得sinα=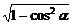 =
=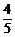 ,
,
tan =
=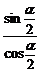 =
=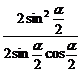 =
=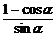 =
=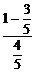 =
=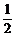 .
.
解析二:tan =
=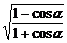 =
=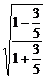 =
=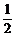 .
.
答案: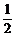
3.若f(tanx)=sin2x,则f(-1)的值是
A.-sin2 B.-1 C.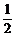 D.1
D.1
解析:f(-1)=f[tan(-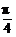 )]=-sin
)]=-sin =-1.
=-1.
答案:B
2.设a=sin14°+cos14°,b=sin16°+cos16°,c=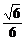 ,则a、b、c的大小关系是
,则a、b、c的大小关系是
A.a<b<c B.a<c<b
C.b<c<a D.b<a<c
解析:a=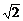 sin59°,c=
sin59°,c=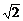 sin60°,b=
sin60°,b=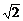 sin61°,∴a<c<b.
sin61°,∴a<c<b.
答案:B
1.下列各式中,值为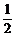 的是
的是
A.sin15°cos15° B.2cos2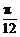 -1
-1
C.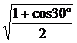 D.
D.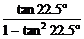
解析: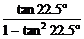 =
=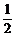 tan45°=
tan45°=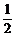 .
.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com