
题目列表(包括答案和解析)
3. 直线l1: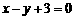 ,l2:
,l2: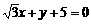 的夹角是( )
的夹角是( )
A.15° B.60° C.75° D. 105°
2. 已知M(– 4,3),N(2,15),则直线MN的斜率是( )
A.2 B.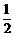 C.– 2 D.
C.– 2 D.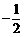
只有一项是符合题目要求的.
1. 若点A(7,3),B(– 1,– 1),则AB中点C的纵坐标为( )
A.3 B.1 C.(3,1) D.(6,2)
(17)(本小题满分10分)
在锐角△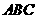 中,角
中,角 、
、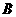 、
、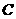 所对的边分别为
所对的边分别为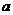 、
、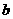 、
、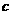 ,已知
,已知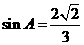 .
.
(Ⅰ)求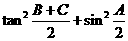 的值;
的值;
(Ⅱ)若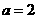 ,△
,△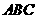 的面积为
的面积为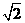 ,求
,求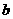 的值.
的值.
(18)(本小题满分12分)
袋中装有若干个质地均匀大小相同的红球和白球,白球数量是红球数量的两倍.每次从袋中摸出一个球,然后放回.若累计3次摸到红球则停止摸球,否则继续摸球直至第5次摸球后结束.
(Ⅰ)求摸球3次就停止的事件发生的概率;
(Ⅱ)记摸到红球的次数为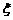 ,求随机变量
,求随机变量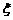 的分布列及其期望.
的分布列及其期望.
(19)(本小题满分12分)
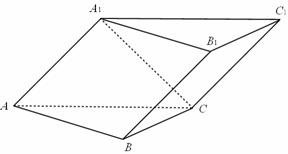 如图,三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,AB=BC=CA=4,且AA1⊥A1C,AA1=A1C.
如图,三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,AB=BC=CA=4,且AA1⊥A1C,AA1=A1C.
(Ⅰ)求侧棱AA1与底面ABC所成角的大小;
(Ⅱ)求侧面A1ABB1与底面ABC所成二面角的大小;
(Ⅲ)求顶点C到侧面A1ABB1的距离.
(20)(本小题满分12分)
已知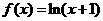 ,
,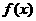 的反函数为
的反函数为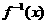 .
.
(I)求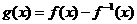 的单调区间;
的单调区间;
(II)若对任意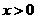 ,不等式
,不等式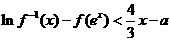 恒成立,求实数
恒成立,求实数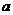 的取值范围.
的取值范围.
(21)(本小题满分12分)
设数列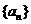 的前
的前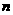 项和
项和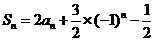 ,
,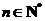 .
.
(Ⅰ)求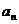 和
和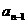 的关系式;
的关系式;
(Ⅱ)求数列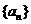 的通项公式;
的通项公式;
(Ⅲ)证明: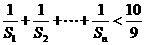 ,
,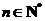 .
.
(22)(本小题满分12分)
已知直线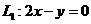 ,
,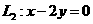 .动圆(圆心为M)被
.动圆(圆心为M)被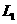 ,
,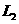 截得的弦长
分别为8,16.
截得的弦长
分别为8,16.
(Ⅰ)求圆心M的轨迹方程M;
(Ⅱ)设直线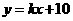 与方程M的曲线相交于A,B两点.如果抛物线
与方程M的曲线相交于A,B两点.如果抛物线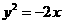 上存在点N使得
上存在点N使得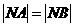 成立,求k的取值范围.
成立,求k的取值范围.
(13)不等式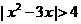 的解集是_________.
的解集是_________.
(14)正四棱锥的各棱长都为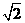 ,各顶点都在同一个球面上,则该球的表面积为________.
,各顶点都在同一个球面上,则该球的表面积为________.
(15)设双曲线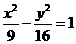 的右顶点为A,右焦点为F,过点F平行于双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为 .
的右顶点为A,右焦点为F,过点F平行于双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为 .
(16)关于函数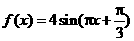 ,
, ,有下列命题:
①对任意
,有下列命题:
①对任意 ,有
,有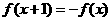 成立;
②
成立;
②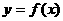 在区间
在区间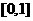 上的最小值为-4;
③
上的最小值为-4;
③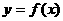 的图象关于点
的图象关于点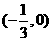 对称;
④
对称;
④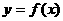 的图象关于直线
的图象关于直线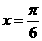 对称.
其中正确的命题的序号是_______.(注:把你认为正确的命题的序号都填上.)
对称.
其中正确的命题的序号是_______.(注:把你认为正确的命题的序号都填上.)
(1)已知集合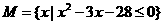 ,
,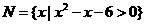 ,则M∩N
为
,则M∩N
为
(A)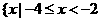 ,或
,或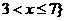 (B)
(B)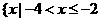 ,或
,或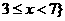
(C)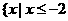 ,或
,或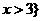 (D)
(D)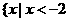 ,或
,或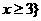
(2)函数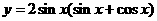 的最大值为
的最大值为
(A)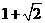 (B)
(B)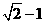 (C)
(C)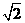 (D)2
(D)2
(3)设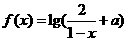 是奇函数,则使
是奇函数,则使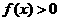 的
的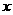 的取值范围是
的取值范围是
(A)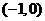 (B)
(B)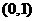 (C)
(C)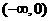 (D)
(D)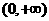
(4)以双曲线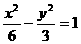 的右焦点为圆心与渐近线相切的圆的方程是
的右焦点为圆心与渐近线相切的圆的方程是
(A)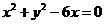 (B)
(B)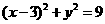
(C)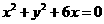 (D)
(D)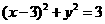
(5)为了得到函数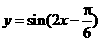 的图象,可以将函数
的图象,可以将函数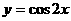 的图象
的图象
(A)向右平移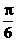 个单位长度 (B)向右平移
个单位长度 (B)向右平移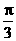 个单位长度
个单位长度
(C)向左平移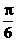 个单位长度 (D)向左平移
个单位长度 (D)向左平移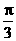 个单位长度
个单位长度
(6)设 ,
,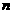 是不同的直线,
是不同的直线,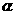 ,
,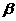 是不同的平面,给出下列命题:
是不同的平面,给出下列命题:
① 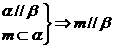 ②
② 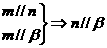
③
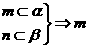 ,
,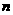 异面
④
异面
④ 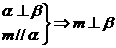
其中假命题有
(A)0个 (B)1个 (C)2个 (D)3个
(7)设椭圆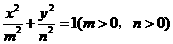 的右焦点与抛物线
的右焦点与抛物线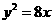 的焦点相同,离心率为
的焦点相同,离心率为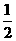 ,则此椭圆的方程为
,则此椭圆的方程为
(A)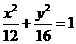 (B)
(B)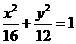 (C)
(C)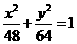 (D)
(D)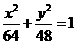
(8)在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为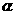 ,则
,则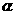 =
=
(A)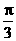 (B)
(B)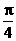 (C)
(C)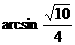 (D)
(D)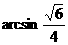
(9)若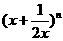 的展开式中前三项的系数成等差数列,则展开式中
的展开式中前三项的系数成等差数列,则展开式中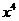 项的系数为
项的系数为
(A)6 (B)7 (C) 8 (D)9
(10)设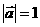 ,
,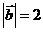 ,
,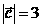 ,且
,且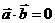 ,则
,则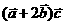 的最小值为
的最小值为
(A)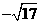 (B)
(B)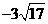 (C)
(C)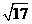 (D)
(D)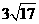
(11)设变量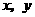 满足约束条件
满足约束条件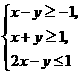 ,则目标函数
,则目标函数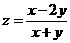 的最大值为
的最大值为
(A)-2 (B)0 (C)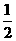 (D)
(D)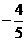
(12)经过平行六面体的任意两个顶点的直线共28条,其中异面直线有
(A)180对 (B)174对 (C)192对 (D)210对
第Ⅱ卷
21.(本小题满分14分)
在△ABC中,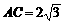 ,B是椭圆
,B是椭圆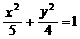 的上顶点,直线l的方程是
的上顶点,直线l的方程是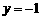 .当AC在直线l上运动时.
.当AC在直线l上运动时.
(Ⅰ)当点C运动到椭圆上时,求线段BC的长度;
(Ⅱ)求△ABC外接圆的圆心P的轨迹E的方程;
(Ⅲ)过定点F(0,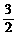 )作互相垂直的直线l1、l2,分别交轨迹E于M、N和R、Q.求四边形MRNQ的面积的最小值.
)作互相垂直的直线l1、l2,分别交轨迹E于M、N和R、Q.求四边形MRNQ的面积的最小值.
福建省龙岩一中09-10学年高二上学期第二学段
20. (本小题满分14分)
(本小题满分14分)
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且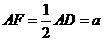 ,G是EF的中点.
,G是EF的中点.
(Ⅰ)求证平面AGC⊥平面BGC;
(Ⅱ)求GB与平面AGC所成角正弦值;
(Ⅲ)求二面角B-AC-G的平面角的正弦值
19.(本小题满分13分)
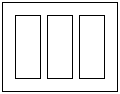
为了迎世博,要设计如图的一张矩形广告,该广告含有大小相等的左中右三个矩形栏目,这三栏的面积之和为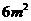 ,四周空白的宽度为
,四周空白的宽度为 ,栏与栏之间的中缝空白的宽度为
,栏与栏之间的中缝空白的宽度为 ,怎样确定广告矩形栏目高与宽的尺寸(单位:
,怎样确定广告矩形栏目高与宽的尺寸(单位: ),能使整个矩形广告面积最小.
),能使整个矩形广告面积最小.
18.(本小题满分13分)
已知椭圆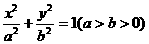 的离心率为
的离心率为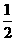 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为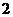 .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)若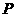 是该椭圆上的一个动点,
是该椭圆上的一个动点,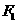 、
、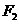 分别是椭圆的左、右焦点,求
分别是椭圆的左、右焦点,求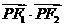 的最大值与最小值.
的最大值与最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com