
题目列表(包括答案和解析)
3、已知圆柱的底面半径为1,母线长为2,则圆柱的侧面积为 ( )
A. 2
B. 4 C.
 D.
D.
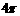
2、计算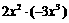 的结果是
( )
的结果是
( )
A. 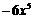 B.
B. 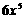 C.
C.
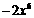 D.
D. 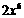
1、如果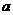 的相反数是2,那么
的相反数是2,那么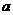 等于
( )
等于
( )
A. -2
B. 2 C.
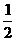 D.
D.
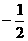
22、(2011•南充)抛物线y=ax2+bx+c与x轴的交点为A(m﹣4,0)和B(m,0),与直线y=﹣x+p相交于点A和点C(2m﹣4,m﹣6).
(1)求抛物线的解析式;
(2)若点P在抛物线上,且以点P和A,C以及另一点Q为顶点的平行四边形ACQP面积为12,求点P,Q的坐标;
(3)在(2)条件下,若点M是x轴下方抛物线上的动点,当△PQM的面积最大时,请求出△PQM的最大面积及点M的坐标.
考点:二次函数综合题;解二元一次方程组;二次函数的最值;待定系数法求二次函数解析式;平行四边形的性质。
专题:计算题;代数几何综合题。
分析:(1)把点A(m﹣4,0)和C(2m﹣4,m﹣6)代入直线y=﹣x+p上得到方程组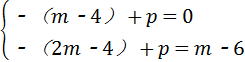 ,求出方程组的解
,求出方程组的解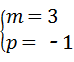 ,得出A、B、C的坐标,设抛物线y=ax2+bx+c=a(x﹣3)(x+1),把C(2,﹣3)代入求出a即可;
,得出A、B、C的坐标,设抛物线y=ax2+bx+c=a(x﹣3)(x+1),把C(2,﹣3)代入求出a即可;
(2)AC所在直线的解析式为:y=﹣x﹣1,根据平行四边形ACQP的面积为12,求出AC边上的高为2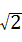 ,过点D作DK⊥AC与PQ所在直线相交于点K,求出DK、DN,得到PQ的解析式为
,过点D作DK⊥AC与PQ所在直线相交于点K,求出DK、DN,得到PQ的解析式为
y=﹣x+3或y=﹣x﹣5,求出方程组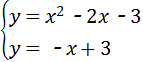 的解即可得到P1(3,0),P2(﹣2,5),根据ACPQ是平行四边形,求出Q的坐标;
的解即可得到P1(3,0),P2(﹣2,5),根据ACPQ是平行四边形,求出Q的坐标;
(3)设M(t,t2﹣2t﹣3),(﹣1<t<3),过点M作y轴的平行线,交PQ所在直线雨点T,则T(t,﹣t+3),求出MT=﹣t2+t+6,过点M作MS⊥PQ所在直线于点S,求出
MS=﹣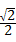 (t﹣
(t﹣ )2+
)2+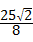 ,即可得到答案.
,即可得到答案.
解答:解:(1)∵点A(m﹣4,0)和C(2m﹣4,m﹣6)在直线y=﹣x+p上
∴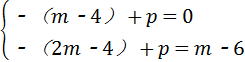
,解得: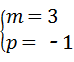 ,
,
∴A(﹣1,0),B(3,0),C(2,﹣3),
设抛物线y=ax2+bx+c=a(x﹣3)(x+1),
∵C(2,﹣3),代入得:﹣3=a(2﹣3)(2+1),
∴a=1
∴抛物线解析式为:y=x2﹣2x﹣3,
答:抛物线解析式为y=x2﹣2x﹣3.
(2)解:AC=3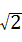 ,
,
AC所在直线的解析式为:y=﹣x﹣1,
∠BAC=45°,
∵平行四边形ACQP的面积为12,
∴平行四边形ACQP中AC边上的高为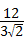 =2
=2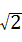 ,
,
过点D作DK⊥AC与PQ所在直线相交于点K,DK=2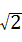 ,
,
∴DN=4,
∵ACPQ,PQ所在直线在直线ACD的两侧,可能各有一条,
∴PQ的解析式或为y=﹣x+3或y=﹣x﹣5,
∴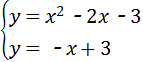 ,
,
解得: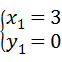 或
或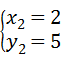 ,
,
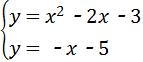 ,方程无解,
,方程无解,
即P1(3,0),P2(﹣2,5),
∵ACPQ是平行四边形,A(﹣1,0),C(2,﹣3),
∴当P(3,0)时,Q(6,﹣3),
当P(﹣2,5)时,Q(1,2),
∴满足条件的P,Q点是P1(3,0),Q1(6,﹣3)或P2(﹣2,5),Q2(1,2)
答:点P,Q的坐标是P1(3,0),Q1(6,﹣3)或P2(﹣2,5),Q2(1,2).
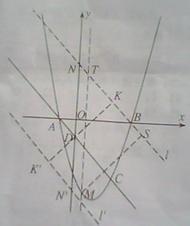 (3)解:设M(t,t2﹣2t﹣3),(﹣1<t<3),
(3)解:设M(t,t2﹣2t﹣3),(﹣1<t<3),
过点M作y轴的平行线,交PQ所在直线雨点T,则T(t,﹣t+3),
MT=(﹣t+3)﹣(t2﹣2t﹣3)=﹣t2+t+6,
过点M作MS⊥PQ所在直线于点S,
MS=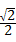 MT=
MT=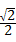 (﹣t2+t+6)=﹣
(﹣t2+t+6)=﹣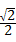 (t﹣
(t﹣ )2+
)2+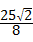 ,
,
∴当t= 时,M(
时,M( ,﹣
,﹣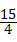 ),△PQM中PQ边上高的最大值为
),△PQM中PQ边上高的最大值为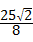 ,
,
答:△PQM的最大面积是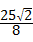 ,,点M的坐标是(
,,点M的坐标是( ,﹣
,﹣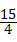 ).
).
点评:本题主要考查对用待定系数法求二次函数的解析式,二次函数的最值,平行四边形的性质,解二元一次方程组等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,此题是一个综合性比较强的题目,有一定的难度.
21、(2011•南充)如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
(1)求证:△MDC是等边三角形;
(2)将△MDC绕点M旋转,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,点E,F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
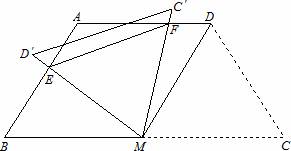
考点:等腰梯形的性质;全等三角形的判定与性质;等边三角形的判定与性质;旋转的性质。
专题:证明题;几何综合题。
分析:(1)过点D作DP⊥BC,于点P,过点A作AQ⊥BC于点Q,得到CP=BQ= AB,CP+BQ=AB,根据ADPQ是矩形,AD=PQ,推出BC=2AD,由点M是BC的中点,推出BM=CM=AD=AB=CD,根据等边三角形的判定即可得到答案;
AB,CP+BQ=AB,根据ADPQ是矩形,AD=PQ,推出BC=2AD,由点M是BC的中点,推出BM=CM=AD=AB=CD,根据等边三角形的判定即可得到答案;
(2)△AEF的周长存在最小值,理由是连接AM,由ABMD是菱形,得出△MAB,△MAD和△MC′D′是等边三角形,推出∠BME=∠AMF,证出△BME≌△AMF(ASA),得出BE=AF,ME=MF,推出△EMF是等边三角形,根据MF的最小值为点M到AD的距离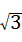 ,即EF的最小值是
,即EF的最小值是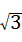 ,即可求出△AEF的周长.
,即可求出△AEF的周长.
解答:(1)证明:过点D作DP⊥BC,于点P,过点A作AQ⊥BC于点Q,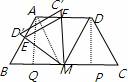
∵∠C=∠B=60°
∴CP=BQ= AB,CP+BQ=AB,
AB,CP+BQ=AB,
又∵ADPQ是矩形,AD=PQ,
故BC=2AD,
由已知,点M是BC的中点,
BM=CM=AD=AB=CD,
即△MDC中,CM=CD,∠C=60°,
故△MDC是等边三角形.
(2)解:△AEF的周长存在最小值,理由如下:
连接AM,由(1)平行四边形ABMD是菱形,
△MAB,△MAD和△MC′D′是等边三角形,
∠BMA=∠BME+∠AME=60°,∠EMF=∠AMF+∠AME=60°,
∴∠BME=∠AMF,
在△BME与△AMF中,BM=AM,∠EBM=∠FAM=60°,
∴△BME≌△AMF(ASA),
∴BE=AF,ME=MF,AE+AF=AE+BE=AB,
∵∠EMF=∠DMC=60°,故△EMF是等边三角形,EF=MF,
∵MF的最小值为点M到AD的距离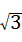 ,即EF的最小值是
,即EF的最小值是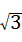 ,
,
△AEF的周长=AE+AF+EF=AB+EF,
△AEF的周长的最小值为2+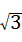 ,
,
答:存在,△AEF的周长的最小值为2+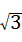 .
.
点评:本题主要考查对等边三角形的性质和判定,旋转的性质,全等三角形的性质和判定,等腰梯形的性质等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.
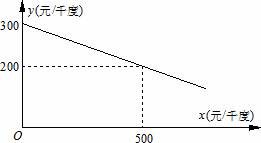
20、(2011•南充)某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图:
(1)当电价为600元千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=10m+500,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
考点:二次函数的应用;一次函数的应用。
专题:应用题。
分析:(1)把(0,300),(500,200)代入直线解析式可得一次函数解析式,把x=600代入函数解析式可得利润的值;
(2)利润=用电量×每千度电产生利润,结合该工厂每天用电量不超过60千度,得到利润的最值即可.
解答:解:(1)工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数解析式为:
y=kx+b.(1分)
该函数图象过点(0,300),(500,200),
∴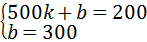 ,
,
解得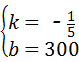 .
.
∴y=﹣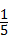 x+300(x≥0).(3分)
x+300(x≥0).(3分)
当电价x=600元/千度时,该工厂消耗每千度电产生利润y=﹣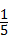 ×600+300=180(元/千度).(4分)
×600+300=180(元/千度).(4分)
(2)设工厂每天消耗电产生利润为w元,由题意得:
W=my=m(﹣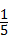 x+300)=[m﹣
x+300)=[m﹣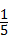 (10m+500)+300].(5分)
(10m+500)+300].(5分)
化简配方,得:w=﹣2(m﹣50)2+5000.(6分)
由题意,m≤60,
∴当m=50时,w最大=5000,
即当工厂每天消耗50千度电时,工厂每天消耗电产生利润为5000元.(8分)
点评:考查二次函数及一次函数的应用;得到总利润的等量关系是解决本题的关键;注意利用配方法解决二次函数的最值问题.
19、(2011•南充)如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABE∽△DFE
(2)若sin∠DFE=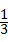 ,求tan∠EBC的值.
,求tan∠EBC的值.
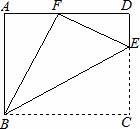
考点:相似三角形的判定与性质;矩形的性质;翻折变换(折叠问题);解直角三角形。
专题:应用题;证明题。
分析:(1)根据矩形的性质可知∠A=∠D=∠C=90°,△BCE沿BE折叠为△BFE,得出∠BFE=∠C=90°,再根据三角形的内角和为180°,可知∠AFB+∠ABF=90°,得出∠ABF=∠DFE,即可证明△ABE∽△DFE,
(2)sin∠DFE=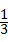 ,设DE=a,EF=3a,DF=
,设DE=a,EF=3a,DF=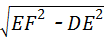 =2
=2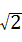 a,可得出CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,由(1)中△ABE∽△DFE,可得tan∠EBC=tan∠EBF=
a,可得出CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,由(1)中△ABE∽△DFE,可得tan∠EBC=tan∠EBF=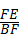 =
=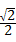 .
.
解答:(1)证明:∵四边形ABCD是矩形
∴∠A=∠D=∠C=90°,
∵△BCE沿BE折叠为△BFE,
∴∠BFE=∠C=90°,
∴∠AFB+∠DFE=180°﹣∠BFE=90°,
又∠AFB+∠ABF=90°,
∴∠ABF=∠DFE,
∴△ABE∽△DFE,
(2)解:在Rt△DEF中,sin∠DFE=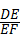 =
=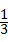 ,
,
∴设DE=a,EF=3a,DF=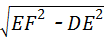 =2
=2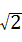 a,
a,
∵△BCE沿BE折叠为△BFE,
∴CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,
又由(1)△ABE∽△DFE,
∴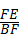 =
=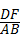 =
=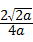 =
=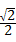 ,
,
∴tan∠EBF=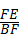 =
=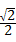 ,
,
tan∠EBC=tan∠EBF=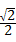 .
.
点评:本题考查了矩形的性质以及相似三角形的证明方法,以及直角三角形中角的函数值,难度适中.
18、(2011•南充)关于的一元二次方程x2+2x+k+1=0的实数解是x1和x2.
(1)求k的取值范围;
(2)如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.
考点:根与系数的关系;根的判别式;解一元一次不等式组。
专题:代数综合题。
分析:(1)方程有两个实数根,必须满足△=b2﹣4ac≥0,从而求出实数k的取值范围;
(2)先由一元二次方程根与系数的关系,得x1+x2=﹣2,x1x2=k+1.再代入不等式x1+x2﹣x1x2<﹣1,即可求得k的取值范围,然后根据k为整数,求出k的值.
解答:解:(1)∵方程有实数根,
∴△=22﹣4(k+1)≥0,(2分)
解得k≤0.
故K的取值范围是k≤0.(4分)
(2)根据一元二次方程根与系数的关系,得x1+x2=﹣2,x1x2=k+1(5分)
x1+x2﹣x1x2=﹣2﹣(k+1).
由已知,得﹣2﹣(k+1)<﹣1,解得k>﹣2.(6分)
又由(1)k≤0,
∴﹣2<k≤0.(7分)
∵k为整数,
∴k的值为﹣1和0.(8分)
点评:本题综合考查了根的判别式和根与系数的关系.在运用一元二次方程根与系数的关系解题时,一定要注意其前提是此方程的判别式△≥0.
17、如图,等腰梯形ABCD中,AD∥BC,点E,F在BC上,且BE=FC,连接DE,AF.求证:DE=AF.

考点:等腰梯形的性质;全等三角形的判定与性质。
专题:证明题。
分析:先根据等腰梯形的性质获得△ABF≌△DCE所需要的条件,再利用全等的性质得到DE=AF.
解答:证明:∵四边形ABCD为等腰梯形且AD∥BC,
∴AB=DC∠B=∠C,(1分)
又∵BE=FC,
∴BE+EF=FC+EF即BF=CE,(2分)
∴△ABF≌△DCE,(3分)
∴DE=AF.(4分)
点评:本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
16、(2011•南充)在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1,2,3,4.随机地摸取出一张纸牌然后放回,在随机摸取出一张纸牌,(1)计算两次摸取纸牌上数字之和为5的概率;
(2)甲、乙两个人进行游戏,如果两次摸出纸牌上数字之和为奇数,则甲胜;如果两次摸出纸牌上数字之和为偶数,则乙胜.这是个公平的游戏吗?请说明理由.
考点:游戏公平性;列表法与树状图法。
专题:计算题。
分析:(1)先列表展示所有可能的结果数为16,再找出两次摸取纸牌上数字之和为5的结果数,然后根据概率的概念计算即可;
(2)从表中找出两次摸出纸牌上数字之和为奇数的结果数和两次摸出纸牌上数字之和为偶数的结果数,分别计算这两个事件的概率,然后判断游戏的公平性.
解答:解:根据题意,列表如下:
|
甲 乙 |
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
5 |
|
2 |
3 |
4 |
5 |
6 |
|
.3 |
4 |
5 |
6 |
7 |
|
4 |
5 |
6 |
7 |
8 |
(2分)
由上表可以看出,摸取一张纸牌然后放回,再随机摸取出纸牌,可能结果有16种,它们出现的可能性相等.
(1)两次摸取纸牌上数字之和为5(记为事件A)有4个,P(A)=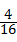 =
=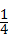 ;
;
(2)这个游戏公平,理由如下:
∵两次摸出纸牌上数字之和为奇数(记为事件B)有8个,P(B)=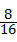 =
= ,
,
两次摸出纸牌上数字之和为偶数(记为事件C)有8个,P(C)=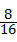 =
= ,
,
∴两次摸出纸牌上数字之和为奇数和为偶数的概率相同,所以这个游戏公平.
点评:本题考查了关于游戏公平性的问题:先利用图表或树形图展示所有可能的结果数,然后计算出两个事件的概率,若它们的概率相等,则游戏公平;若它们的概率不相等,则游戏不公平.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com