
题目列表(包括答案和解析)
12.解析:
f′(x)=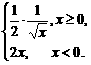 ∴f′(1)·f′(-1)=-1. 答案: C
∴f′(1)·f′(-1)=-1. 答案: C
11.解析: 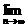 (a·
(a·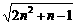 -nb)=
-nb)=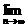
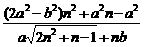 存在,
存在,
则2a2-b2=0. ①
∴原式=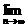
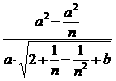 =1. ∴
=1. ∴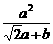 =1. ②
=1. ②
由①②可知,a=2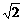 ,b=4.
∴ab=8
,b=4.
∴ab=8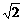 . 答案: A
. 答案: A
10.解析: 满足几何分布,∴Eξ=np=14.7.∴B满足. 答案: B
9.解析: 由已知|x|≤2,则-2≤x≤2.
当x=-2,2时,y=0.有2个;
当x=-1,1时,y=0,1.有4个;
当x=0时,y=0,1,2.有3个.
综上,共有9个,故选D.
8.解析: 令y=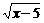 ,y=kx,显然k≤0时成立,
,y=kx,显然k≤0时成立,
由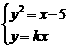
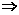 k2x2-x+5=0(k>0), 由Δ=0,得k=
k2x2-x+5=0(k>0), 由Δ=0,得k=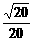 ; 由
; 由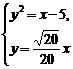 得x=10,而x≥15,
得x=10,而x≥15,
∴当x=15时,k=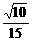 . ∴k≤0或k>
. ∴k≤0或k>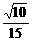 . 答案: C
. 答案: C
7.解析: 把棱长为3 cm的正方体分割成棱长为1 cm的正方体共有33=27个,如题意抽去三个方向上的正方体,余下的可分为两类.
第一类:处于正方体8个顶点上的8个小正方体,它们算入表面积的面各3个,共3×8=24(cm2);第二类:处于正方体各棱中间的正方体,每个正方体算入表面积的面各4个,共4×12=48(cm2),则总表面积为24+48=72(cm2).
注:此题另一种思路是:外表面积8×6=48(cm2),内表面积2×12=24(cm2),总表面积 72 cm2. 答案: B
6.解析: y=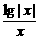 是奇函数,且当x=±1时,y=0,所以选D. 答案: D
是奇函数,且当x=±1时,y=0,所以选D. 答案: D
5.解析: 构造函数:an=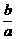 (1-
(1-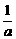 ·
·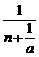 ), 由a>0,b<0知an是关于n的减函数, ∴an>an+1. 答案: A
), 由a>0,b<0知an是关于n的减函数, ∴an>an+1. 答案: A
4.解析: 由题设得4a·c-2b·c=4·3-2b·c=(-2,2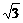 )·(1,
)·(1, 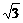 ),
),
故得b·c=4.
所以cosθ=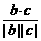 =
=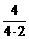 =
= 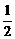
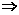 θ=
θ=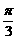 , 故选B
, 故选B
本题主要考查向量数量积的坐标运算及向量数量积公式的灵活应用.
3.解析: |AB|=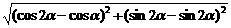 =2|sin
=2|sin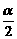 |=1. 答案: C
|=1. 答案: C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com