
题目列表(包括答案和解析)
8.“a>2且b>2”是“a+b>4且ab>4”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:当a=3,b=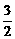 时,满足a+b>4且ab>4,但不满足a>2且b>2.
时,满足a+b>4且ab>4,但不满足a>2且b>2.
答案:A
7.如果命题“p或q”是真命题,命题“p且q”是假命题,那么
A.命题p和命题q都是假命题 B.命题p和命题q都是真命题
C.命题p和命题“非q”真值不同 D.命题p和命题“非q”真值相同
解析:p或q中有一个真命题,一个假命题.
答案:D
6.已知数列{an},那么“对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上”是“{an}为等差数列”的
A.必要而不充分条件 B.充分而不必要条件
C.充要条件 D.既不充分也不必要条件
解析:点Pn(n,an)都在直线y=2x+1上,即an=2n+1.
∴{an}为等差数列,但是{an}是等差数列却不一定就是an=2n+1.
∴是充分不必要条件.
答案:B
5.(2003年合肥模拟题)给出命题p:3≥3,q:函数f(x)=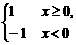 在R上是连续函数,则在下列三个复合命题“p且q”“p或q”“非p”中,真命题的个数为
在R上是连续函数,则在下列三个复合命题“p且q”“p或q”“非p”中,真命题的个数为
A.0 B.1 C.2 D.3
解析:p真q假.
答案:B
4.(2005年启东市高三年级第二次调研考试)已知集合A={x|x=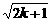 ,k∈N},B={x|x≤4,x∈Q},则A∩B为
,k∈N},B={x|x≤4,x∈Q},则A∩B为
A.{0,3} B.{1,3}
C.{1,4} D.{1,2,3,4}
解析:由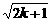 ≤4,得2k≤15,k≤7.5.又k∈N,∴k∈{0,1,2,3,4,5,6,7}.又只有k=0或k=4时能使x∈Q,∴A∩B={1,3}.
≤4,得2k≤15,k≤7.5.又k∈N,∴k∈{0,1,2,3,4,5,6,7}.又只有k=0或k=4时能使x∈Q,∴A∩B={1,3}.
答案:B
3.设M={1,2,m2-3m-1},P={-1,3},M∩P={3},则m的值为
A.4 B.-1 C.1,-4 D.4,-1
解析:∵M∩P={3},∴3∈M.
∴m2-3m-1=3.∴m=4或m=-1.
答案:D
2.下列四个命题,其中正确命题的个数为
①与1非常接近的全体实数能构成集合 ②{-1,(-1)2}表示一个集合 ③空集是任何一个集合的真子集 ④任何两个非空集合必有两个以上的子集
A.0 B.1 C.2 D.3
解析:命题②④正确.
答案:C
1.(2004年北京,1)设全集是实数集R,M={x|-2≤x≤2},N={x|x<1},则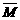 ∩N等于
∩N等于
A.{x|x<-2} B.{x|-2<x<1}
C.{x|x<1} D.{x|-2≤x<1}
解析:∵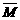 ={x|x<-2或x>2},∴
={x|x<-2或x>2},∴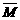 ∩N={x|x<-2}.
∩N={x|x<-2}.
答案:A
14.(14分)已知(1+3x)n的展开式中,末三项的二项式系数的和等于121,求展开式中系数最大的项及二项式系数最大的项.
解:末三项的二项式系数分别为C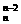 、C
、C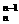 、C
、C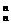 ,
,
由题设,得C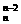 +C
+C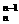 +C
+C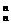 =121,
=121,
即C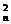 +C
+C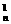 +1=121,∴n2+n-240=0.
+1=121,∴n2+n-240=0.
∴n=15(n=-16舍去).
∵T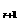 =C
=C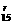 (3x)r=C
(3x)r=C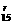 ·3rxr,
·3rxr,
设T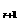 项与Tr项的系数分别为t
项与Tr项的系数分别为t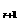 与tr,
与tr,
则t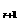 =C
=C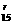 3r,tr=C
3r,tr=C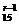 ·3
·3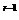 ,令
,令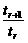 >1,
>1,
即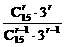 =
=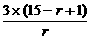 >1,
>1,
解得r<12.
也就是说,当r取小于12的自然数时,都有tr<t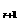 ,即第12项以前的各项,前面一项的系数都比后面一项的系数小.
,即第12项以前的各项,前面一项的系数都比后面一项的系数小.
又当r=12时,t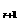 =tr,即t13=t12,
=tr,即t13=t12,
∴展开式中系数最大的项是T12=C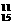 ·311·x11,T13=C
·311·x11,T13=C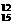 ·312·x12,
·312·x12,
当n=15时,二项式系数最大的是第8、9项,
分别为C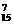 ·37·x7与C
·37·x7与C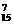 ·38·x8.
·38·x8.
评述:本题考查二项式系数的性质、二项式定理、二项式系数与项的系数以及运算能力.注意二项展开式中,项的系数与项的二项式系数是两个不同的概念,前者由指数、底数二者决定,而后者只与二项式次数有关,一般地,项的系数不具备二项式系数的性质,不能混用.在(a+b)n的展开式中,系数最大的项是中间项;但当a、b的系数不是1时,最大系数值的项的位置就不一定在中间,需要利用通项公式,根据系数值的增减性具体讨论而定.
13.(14分)7名学生站成一排,下列情况各有多少种不同排法?
(1)甲、乙必须排在一起;
(2)甲不在排头,乙不在排尾;
(3)甲、乙、丙互不相邻;
(4)甲、乙之间必须隔一人.
解:(1)(整体排列法)先将甲、乙看作一个人,有A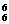 种排法,然后甲、乙换位,所以不同的排法有A
种排法,然后甲、乙换位,所以不同的排法有A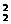 ·A
·A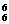 =1440种.
=1440种.
(2)(间接法)甲在排头或乙在排尾的排法共2A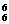 种,其中都包含甲在排头且乙在排尾的情形,故有不同的排法A
种,其中都包含甲在排头且乙在排尾的情形,故有不同的排法A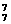 -2A
-2A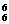 +A
+A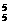 =3720种.
=3720种.
(3)(插空法)把甲、乙、丙插入其余4个元素产生的5个空,有A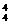 ·A
·A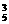 =1440种.
=1440种.
(4)先从其余5人中选1人有5种选法,放在甲、乙之间,将三人看作一个有A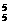 种,然后甲、乙换位有A
种,然后甲、乙换位有A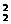 种,共有5A
种,共有5A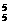 A
A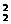 =1200种方法.
=1200种方法.
评述:解决“相邻”问题一般用整体法,解决不相邻问题一般用插空法,解决某些元素在某些位置用定位法,解决某些元素不在某些位置一般用间接法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com