
题目列表(包括答案和解析)
18.(1)解 由已知得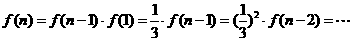
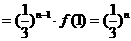 . (4分)
. (4分)
(2)证明 由(1)可 知 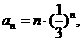 设
设
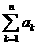
则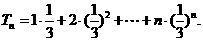
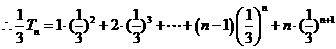 .
.
两式相减得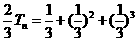 +…+
+…+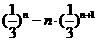
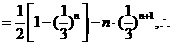

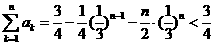 . (9分)
. (9分)
(3)解 由(1)可知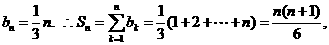
则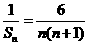 =
=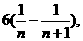
故有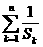
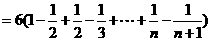 =6
=6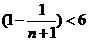 . (14分)
. (14分)
17.解(I)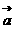 +
+
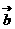 =(x,0)+
=(x,0)+ (1,y)=(x+
(1,y)=(x+ ,
, y),
y),
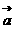 –
–
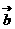 =(x, 0)
=(x, 0)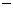
 (1,y)= (x
(1,y)= (x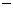
 ,–
,– y).
y). (
(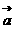 +
+
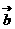 )
)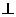 (
(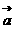
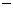

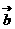 ),
),
 (
(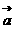 +
+
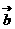 )·(
)·(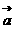
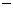

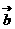 )=0,
)=0,  (x+
(x+ )( x
)( x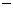
 )+
)+ y·(
y·(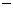
 y)=0,
y)=0,
故P点的轨迹方程为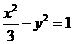 . (6分)
. (6分)
(II)考虑方程组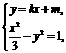 消去y,得(1–3k2)x2-6kmx-3m2-3=0
(*)
消去y,得(1–3k2)x2-6kmx-3m2-3=0
(*)
显然1-3k2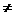 0,
0, 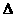 =(6km)2-4(1-3k2)( -3m2-3)=12(m2+1-3k2)>0.
=(6km)2-4(1-3k2)( -3m2-3)=12(m2+1-3k2)>0.
设x1,x2为方程*的两根,则x1+x2=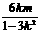 ,x0=
,x0=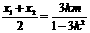 , y0=kx0+m=
, y0=kx0+m=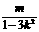 ,
,
故AB中点M的坐标为(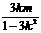 ,
,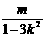 ),
),
 线段AB的垂直平分线方程为y
线段AB的垂直平分线方程为y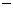
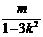 =(
=(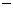
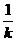 )
)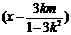 ,
,
将D(0,–1)坐标代入,化简得 4m=3k2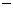 1,
1,
故m、k满足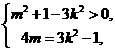 消去k2得 m2
消去k2得 m2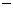 4m>0, 解得 m<0或m>4.
4m>0, 解得 m<0或m>4.
又 4m=3k2
4m=3k2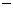 1>
1>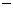 1,
1, 
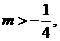 故m
故m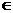 (
(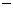
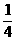 ,0)
,0)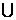 (4,+
(4,+ ). (12分)
). (12分)
16.(1)f1(0)=2,a1=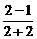 =
=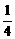 ,fn+1(0)=f1[fn(0)]=
,fn+1(0)=f1[fn(0)]=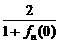 ,
,
an+1=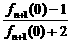 =
= =
=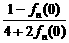 =-
=-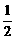
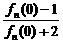 =-
=-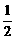 an, 4分
an, 4分
∴数列{an}是首项为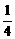 ,公比为-
,公比为-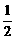 的等比数列,∴an=
的等比数列,∴an=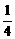 (-
(-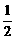 )n-1. 6分
)n-1. 6分
(2)T2n=a1+2a2+3a3+…+(2n-1)a2n-1+2na2n,
-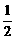 T2n=(-
T2n=(-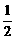 a1)+(-
a1)+(-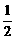 )2a2+(-
)2a2+(-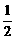 )3a3+…+(-
)3a3+…+(-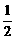 )(2n-1)a2n-1+(-
)(2n-1)a2n-1+(-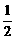 )·2na2n
)·2na2n
=a2+2a3+…+(2n-1)a2n-na2n, 8分
两式相减得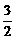 T2n=a1+a2+a3+…+a2n+na2n,
T2n=a1+a2+a3+…+a2n+na2n,
所以,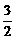 T2n=
T2n=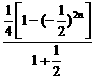 +n×
+n×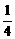 (-
(-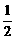 )2n-1=
)2n-1= -
- (-
(-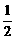 )2n+
)2n+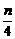 (-
(-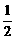 )2n-1, 10分
)2n-1, 10分
T2n=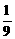 -
-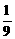 (-
(-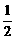 )2n+
)2n+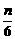 (-
(-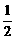 )2n-1=
)2n-1=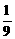 (1-
(1-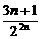 ).
∴9T2n=1-
).
∴9T2n=1-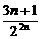 ,
,
Qn=1-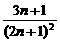 , 12分
, 12分
当n=1时,22n=4,(2n+1)2=9,∴9T2n<Qn;
当n=2时,22n=16,(2n+1)2=25,∴9T2n<Qn; 13分
当n≥3时,22n=[(1+1)n]2
=(C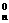 +C
+C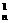 +C
+C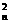 +…+C
+…+C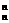 )2>(2n+1)2,∴9T2n>Qn. 14分
)2>(2n+1)2,∴9T2n>Qn. 14分
15.(1)设点M的坐标为(x,y),由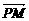 =-
=-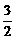
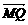 ,得P(0,-
,得P(0,-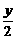 ),Q(
),Q(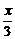 ,0), 2分
,0), 2分
由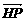 ·
·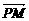 =0,得(3,-
=0,得(3,-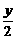 )(x,
)(x,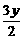 )=0,又得y2=4x, 5分
)=0,又得y2=4x, 5分
由点Q在x轴的正半轴上,得x>0,
所以,动点M的轨迹C是以(0,0)为顶点,以(1,0)为焦点的抛物线,除去原点. 6分
(2)设直线l:y=k(x+1),其中k≠0,代入y2=4x,得k2x2+2(k2-2)x+k2=0,① 7分
设A(x1,y1),B(x2,y2),
则x1,x2是方程①的两个实根,∴x1+x2=-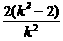 ,x1x2=1,
,x1x2=1,
所以,线段AB的中点坐标为(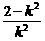 ,
,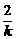 ), 8分
), 8分
线段AB的垂直平分线方程为y-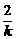 =-
=-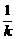 (x-
(x-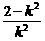 ), 9分
), 9分
令y=0,x0=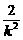 +1,所以点E的坐标为(
+1,所以点E的坐标为(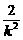 +1,0)
+1,0)
因为△ABE为正三角形,所以点E(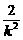 +1,0)到直线AB的距离等于
+1,0)到直线AB的距离等于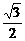 |AB|,
|AB|,
而|AB|=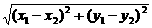 =
=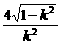 ·
·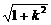 , 10分
, 10分
所以,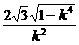 =
=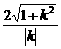 , 11分
, 11分
解得k=±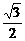 ,得x0=
,得x0=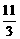 . 12分
. 12分
13.解析:(1)。,由根与系数的关系得,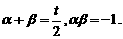
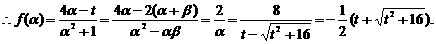
同法得f(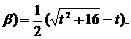
(2).证明: f/(x)=
f/(x)=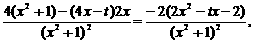 而当x
而当x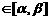 时,
时,
2x2-tx-2=2(x-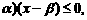 故当x
故当x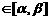 时, f/(x)≥0,
时, f/(x)≥0,
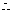 函数f(x)在[
函数f(x)在[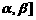 上是增函数。
上是增函数。
(3)。证明:
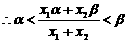 , 同理
, 同理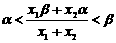 .
.
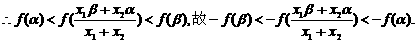
又f(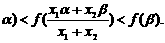 两式相加得:
两式相加得:
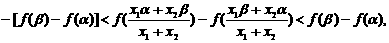
即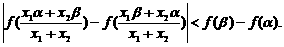
而由(1),f(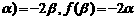 且f(
且f(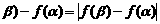 ,
,
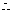
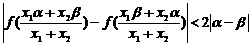 .
.
14(I)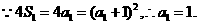 当
当 时,
时,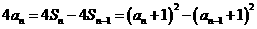 ,
,
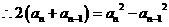 ,又{an}各项均为正数,
,又{an}各项均为正数,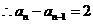 .数列
.数列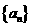 是等差数列,
是等差数列, 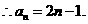
(II)  ,若
,若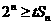 对于任意的
对于任意的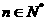 恒成立,则
恒成立,则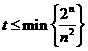 .令
.令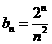 ,.当
,.当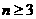 时,
时,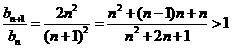 .又
.又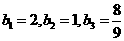 ,
,
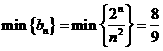 .
.
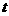 的最大值是
的最大值是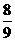 .
.
12.(1)由题意,有x2-2mx+2m2+>0对任意的x∈R恒成立 所以△=4m2-4(2m2+)<0 即-m2-<0 ∴>0 由于分子恒大于0,只需m2-3>0即可 所以m<-或m> ∴M={m|m<-或m>} ……4分 (2)x2-2mx+2m2+=(x-m)2+m2+≥m2+ 当且仅当x=m时等号成立. 所以,题设对数函数的真数的最小值为m2+ ……7分 又因为以3为底的对数函数为增函数 ∴f(x)≥log3(m2+) ∴当且仅当x=m(m∈M)时,f(x)有最小值为log3(m2+) ……10分 又当m∈M时,m2-3>0 ∴m2+=m2-3++3≥2+3=9 当且仅当m2-3=,即m=±时, log3(m2+)有最小值log3(6+)=log39=2 ∴当x=m=±时,其函数有最小值2.
11.设直线OA的斜率为k,显然k存在且不等于0 则OA的方程为y=kx 由解得A() ……4分 又由,知OA⊥OB,所以OB的方程为y=-x 由解得B(2pk2,-2pk) ……4分 从而OA的中点为A'(),OB的中点为B'(pk2,-pk) ……6分 所以,以OA、OB为直径的圆的方程分别为 x2+y2-=0 ……① x2+y2-2pk2x+2pky=0 ……② ……10分 ∵P(x,y)是异于O点的两圆交点,所以x≠0,y≠0 由①-②并化简得y=(k-)x ……③ 将③代入①,并化简得x(k2+-1)=2p ……④ 由③④消去k,有x2+y2-2px=0 ∴点P的轨迹为以(p,0)为圆心,p为半径的圆(除去原点). ……13分
9.解:(Ⅰ)设双曲线C的渐近线方程为y=kx,则kx-y=0
∵该直线与圆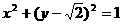 相切,
相切,
∴双曲线C的两条渐近线方程为y=±x.…………………………………………2分
故设双曲线C的方程为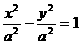 .
.
又双曲线C的一个焦点为 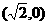
∴ ,
,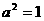 .
.
∴双曲线C的方程为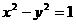 .………………………………………………4分
.………………………………………………4分
(Ⅱ)由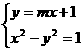 得
得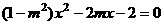 .
.
令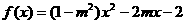
直线与双曲线左支交于两点,等价于方程f(x)=0在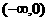 上有两个不等实根.
上有两个不等实根.
因此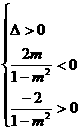 解得
解得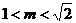 .
.
又AB中点为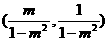 ,
,
∴直线l的方程为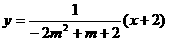 .………………………………6分
.………………………………6分
令x=0,得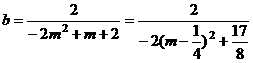 .
.
∵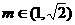 ,
,
∴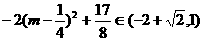
∴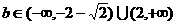 .………………………………………………8分
.………………………………………………8分
(Ⅲ)若Q在双曲线的右支上,则延长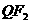 到T,使
到T,使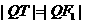 ,
,
若Q在双曲线的左支上,则在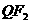 上取一点T,使
上取一点T,使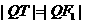 .
.
根据双曲线的定义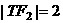 ,所以点T在以
,所以点T在以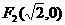 为圆心,2为半径的圆上,即点T的轨迹方程是
为圆心,2为半径的圆上,即点T的轨迹方程是
 ①…………………………………………10分
①…………………………………………10分
由于点N是线段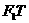 的中点,设
的中点,设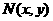 ,
,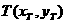 .
.
则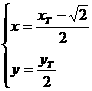 ,即
,即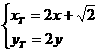 .
.
代入①并整理得点N的轨迹方程为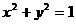 .
.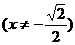 ………………12分
………………12分
10 解:(Ⅰ)因为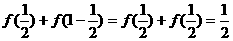 .所以
.所以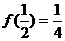 .……2分
.……2分
令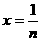 ,得
,得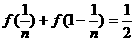 ,即
,即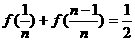 .……………4分
.……………4分
(Ⅱ)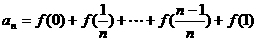
又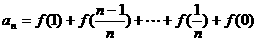 ………………5分
………………5分
两式相加
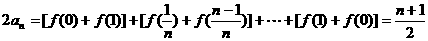 .
.
所以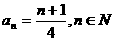 ,………………7分
,………………7分
又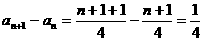 .故数列
.故数列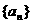 是等差数列.………………9分
是等差数列.………………9分
(Ⅲ)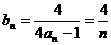

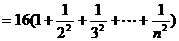
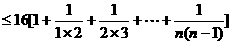 ………………10分
………………10分
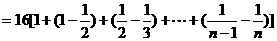 ………………12分
………………12分
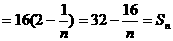
所以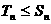 ……………………………………………………………………14分
……………………………………………………………………14分
8.(1)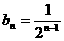
(2)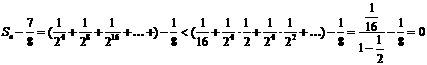
7、解:(1)设动点的坐标为P(x,y),则H(0,y),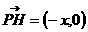 ,
,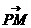 =(-2-x,-y)
=(-2-x,-y)
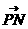 =(2-x,-y)
=(2-x,-y)
∴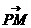 ·
·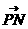 =(-2-x,-y)·(2-x,-y)=
=(-2-x,-y)·(2-x,-y)=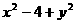
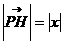
由题意得∣PH∣2=2·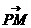 ·
·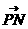
即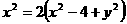
即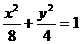 ,所求点P的轨迹为椭圆
,所求点P的轨迹为椭圆
(2)由已知求得N(2,0)关于直线x+y=1的对称点E(1,-1),则∣QE∣=∣QN∣
双曲线的C实轴长2a=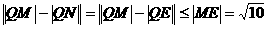 (当且仅当Q、E、M共线时取“=”),此时,实轴长2a最大为
(当且仅当Q、E、M共线时取“=”),此时,实轴长2a最大为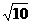
所以,双曲线C的实半轴长a=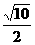
又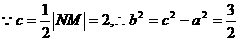
∴双曲线C的方程式为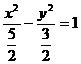
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com