
题目列表(包括答案和解析)
7.在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是
(A)BC//平面PDF (B)DF⊥平面PA E
(C)平面PDF⊥平面ABC (D)平面PAE⊥平面 ABC
6.对任意的锐角α,β,下列不等关系中正确的是
(A)sin(α+β)>sinα+sinβ (B)sin(α+β)>cosα+cosβ
(C)cos(α+β)<sinα+sinβ (D)cos(α+β)<cosα+cosβ
5.从原点向圆 x2+y2-12y+27=0作两条切线,则这两条切线的夹角的大小为
(A)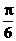 (B)
(B)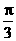 (C)
(C)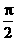 (D)
(D)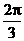
4.若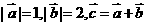 ,且
,且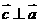 ,则向量
,则向量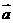 与
与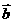 的夹角为
的夹角为
(A)30° (B)60° (C)120° (D)150°
3.“m=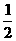 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
(A)充分必要条件 (B)充分而不必要条件
(C)必要而不充分条件 (D)既不充分也不必要条件
2.为了得到函数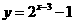 的图象,只需把函数
的图象,只需把函数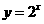 上所有点
上所有点
(A)向右平移3个单位长度,再向下平移1个单位长度
(B)向左平移3个单位长度,再向下平移1个单位长度
(C)向右平移3个单位长度,再向上平移1个单位长度
(D)向左平移3个单位长度,再向上平移1个单位长度
1.设P、Q为两个非空实数集合,定义集合P+Q=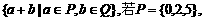
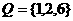 ,则P+Q中元素的个数是
,则P+Q中元素的个数是
A.9 B.8 C.7 D.6
20.(1)由y=x3-3ax2+b x, ①
得y′=3x2-6ax+b.
过曲线①上点P1(x1, y1)的切线l1的方程是
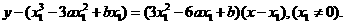
由它过原点,有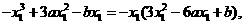
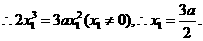
(2)过曲线①上点Pn+1(xn+1,yn+1)的切线ln+1的方程是
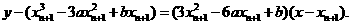
由ln+1过曲线①上点P n(x n, yn),有
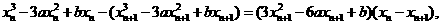
∵x n-xn+1≠0,以x n-xn+1除上式,得
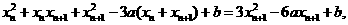
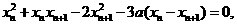 以x n-xn+1除之,得x n+2xn+1-3a=0.
以x n-xn+1除之,得x n+2xn+1-3a=0.
(3)解法1 由(2)得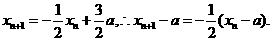
故数列{x n-a}是以x 1-a=为首项,公比为-的等比数列,
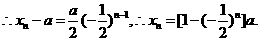
∵a>0,∴当n为正偶数时, 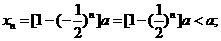
当n为正奇数时, 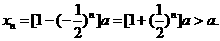
解法2 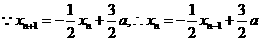 =
=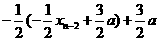
=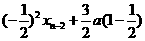 =
=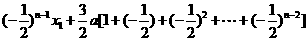
=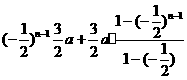 =
=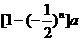 .以下同解法1.
.以下同解法1.
19. 解:(Ⅰ)设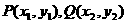 ,而Q1与Q关于x轴对称,则
,而Q1与Q关于x轴对称,则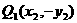
PQ直线方程为: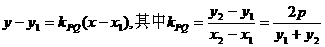
则PQ: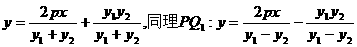
又PQ过点(m,0),则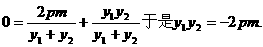
因此PQ1直线方程可改写为: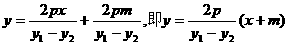
因此可知PQ1直线恒过点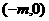
(Ⅱ)连结AQ1,因为Q与Q1关于x轴对称,A在x轴上
所以在△APQ1中,AB平分∠PAQ1.
由内角平分线定理可知: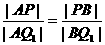
而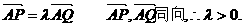
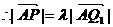 于是
于是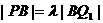
而又B,P,Q1三点共线,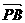 、
、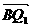 同向,
同向,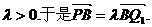
18、解:(1) 法一:由条件知△ABC为直角三角形,且∠BAC = 90°,
 ∵ PA = PB
= PC,
∵ PA = PB
= PC,
∴ 点P在平面ABC上的射影是△ABC的外心,
即斜边BC的中点E.
取AC中点D,连PD, DE, PE.
∵ PE⊥平面ABC,DE⊥AC (∵ DE∥AB),
∵ AC⊥PD.
∴ ∠PDE为二面角P-AC-B的平面角.
又PE = AC ,DE = AC ,(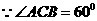 )
)
∴  tan ∠PDE = =
tan ∠PDE = =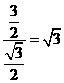 ,
,
∴ ∠PDE = 60°.
故二面角P-AC-B的大小为60°.
法二:由条件知△ABC为直角三角形,且∠BAC = 90°,
∵ PA = PB = PC,
∴ 点P在平面ABC上的射影是△ABC的外心,即斜边BC的中点.
设O为BC中点,则可证明PO⊥平面ABC.
建立如图直角坐标系,设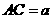 则
则
A( a, a, 0), B(-a, 0, 0), C(a, 0, 0), D(0, 0, a).
= (-a, a, 0), = ( -a, a, a).
取AC中点D,连PD, DO, PO.
∵ AB⊥AC,
又PA = PCÞ PD⊥AC.
∴ cos < , > 即为二面角P-AC-B的余弦值.
而 cos < , > = = .
∴ 二面角P-AC-B的大小为 60°.
(2) 法一:设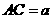 ,则PD = = = a.
,则PD = = = a.
S△APC = AC·PD = a 2.
设点B到平面PAC的距离为h,则由VP-ABC = VB-APC 得
S△ABC·PE = S△ABC·h Þ h = = = a.
故点B到平面PAC的距离为 a.
法二:点E到平面PAC的距离容易求得为 a,而点B到平面PAC的距离是其两倍.
∴ 点B到平面PAC的距离为 a.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com