
题目列表(包括答案和解析)
6.一个圆锥和一个半球有公共底面,如果圆锥的体积与半球的体积恰好相等,则圆锥轴截面顶角的余弦值是( )
A.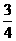 B.
B.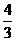 C.
C.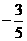 D.
D.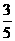
5.在△ABC中,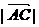 =5,
=5,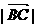 =3,
=3,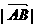 =6,则
=6,则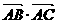 =( )
=( )
A.13 B.26 C.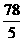 D.24
D.24
4.现用铁丝做一个面积为1平方米、形状为直角三角形的框架,有下列四种长度的铁丝各一根供选择,其中最合理(即够用,浪费最少)的一根是( ).
A.4.6米 B.4.8米 C.5.米 D.5.2米
3.将正方形ABCD沿对角线BD折成120°的二面角,C点到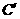 处,这时异面直线AD与
处,这时异面直线AD与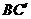 所成角的余弦值是( )
所成角的余弦值是( )
A.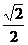 B.
B.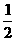 C.
C.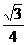 D.
D.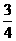
2.若直线mx+ny=4和⊙O∶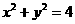 没有交点,则过(m,n)的直线与椭圆
没有交点,则过(m,n)的直线与椭圆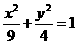 的交点个数( )
的交点个数( )
A.至多一个 B.2个
C.1个 D.0个
1.设a、b、c是任意的非零平面向量,且相互不共线,则( )
①(a·b)c-(c·a)b=0
②|a|-|b|<|a-b|;
③(b·c)a-(c·a)b不与c垂直;
④(3a+2b)·(3a-2b)=9|a|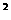 -4|b|
-4|b|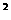 .
.
其中的真命题是( )
A.②④ B.③④ C.②③ D.①②
20.(1)由y=x3-3ax2+b x, ①
得y′=3x2-6ax+b.
过曲线①上点P1(x1, y1)的切线l1的方程是
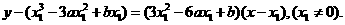
由它过原点,有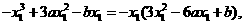
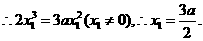 4分
4分
(2)过曲线①上点Pn+1(xn+1,yn+1)的切线ln+1的方程是
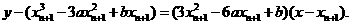
由ln+1过曲线①上点P n(x n, yn),有
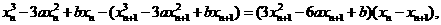
∵x n-xn+1≠0,以x n-xn+1除上式,得
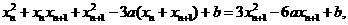
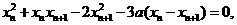 以x n-xn+1除之,得x n+2xn+1-3a=0.
9分
以x n-xn+1除之,得x n+2xn+1-3a=0.
9分
(3)解法1 由(2)得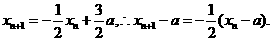
故数列{x n-a}是以x 1-a=为首项,公比为-的等比数列,
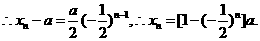
∵a>0,∴当n为正偶数时, 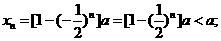
当n为正奇数时, 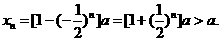 14分
14分
解法2 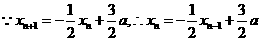 =
=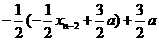
=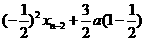 ==
==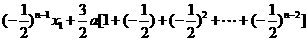 =
=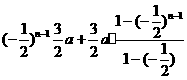 =
=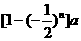 .以下同解法1.
.以下同解法1.
备用题:
已知函数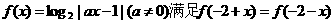 ,则实数a值是( )
,则实数a值是( )
A.1 B.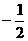 C.
C.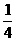 D.-1
D.-1
如图所示,过定点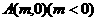 作一直线
作一直线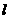 交抛物线C:
交抛物线C: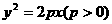 于P、Q两点,又Q关于x轴对称点为Q1,连结PQ1交x轴于B点.
于P、Q两点,又Q关于x轴对称点为Q1,连结PQ1交x轴于B点.
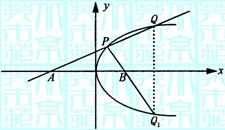 (1)求证:直线PQ1恒过一定点;
(1)求证:直线PQ1恒过一定点;
(2)若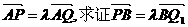 .
.
解:(1)设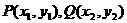 ,而Q1与Q关于x轴对称,则
,而Q1与Q关于x轴对称,则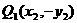 PQ直线方
PQ直线方
程为: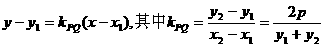
则PQ: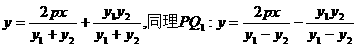
又PQ过点(m,0),则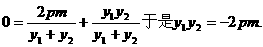
因此PQ1直线方程可改写为: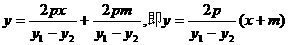
因此可知PQ1直线恒过点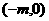 ……………………(8分)
……………………(8分)
(2)连结AQ1,因为Q与Q1关于x轴对称,A在x轴上
所以在△APQ1中,AB平分∠PAQ1. 由内角平分线定理可知: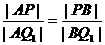
而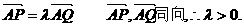
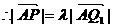 于是
于是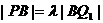
而又B,P,Q1三点共线,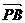 、
、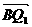 同向,
同向,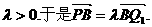 ………(14分)
………(14分)
19. 解:(Ⅰ)设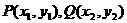 ,而Q1与Q关于x轴对称,则
,而Q1与Q关于x轴对称,则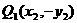 2分
2分
PQ直线方程为: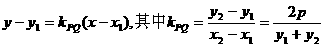
则PQ: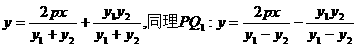
又PQ过点(m,0),则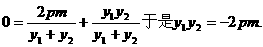
因此PQ1直线方程可改写为: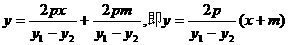
因此可知PQ1直线恒过点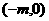 …
…………………(8分)
…
…………………(8分)
(Ⅱ)连结AQ1,因为Q与Q1关于x轴对称,A在x轴上
所以在△APQ1中,AB平分∠PAQ1. 由内角平分线定理可知: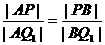
而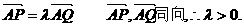
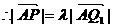 于是
于是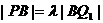
而又B,P,Q1三点共线,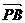 、
、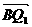 同向,
同向,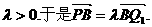 … ……(14分)
… ……(14分)
17、解:(1) 法一:由条件知△ABC为直角三角形,且∠BAC = 90°,
∵ PA = PB = PC,
∴ 点P在平面ABC上的射影是△ABC的外心,
即斜边BC的中点E. 2分
取AC中点D,连PD, DE, PE.
∵ PE⊥平面ABC,DE⊥AC (∵ DE∥AB),
∵ AC⊥PD. 4分
∴ ∠PDE为二面角P-AC-B的平面角. 5分
又PE = AC ,DE = AC ,(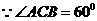 )
)
∴  tan ∠PDE = =
tan ∠PDE = =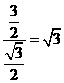 ,
,
∴ ∠PDE = 60°.
故二面角P-AC-B的大小为60°. 8分
法二:由条件知△ABC为直角三角形,且∠BAC = 90°,
∵ PA = PB = PC,
∴ 点P在平面ABC上的射影是△ABC的外心,即斜边BC的中点.
设O为BC中点,则可证明PO⊥平面ABC. 2分
建立如图直角坐标系,设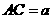 则
则
A( a, a, 0), B(-a, 0, 0), C(a, 0, 0), D(0, 0, a).
= (-a, a, 0), = ( -a, a, a). 4分
取AC中点D,连PD, DO, PO.
∵ AB⊥AC,
又PA = PCÞ PD⊥AC.
∴ cos < , > 即为二面角P-AC-B的余弦值. 6分
而 cos < , > = = .
∴ 二面角P-AC-B的大小为 60°. 8分
(2) 法一:设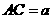 ,则PD = = = a.
,则PD = = = a.
S△APC = AC·PD = a 2. 10分
设点B到平面PAC的距离为h,则由VP-ABC = VB-APC 得
S△ABC·PE = S△ABC·h Þ h = = = a.
故点B到平面PAC的距离为 a. 14分
法二:点E到平面PAC的距离容易求得为 a,而点B到平面PAC的距离是其两倍.
∴ 点B到平面PAC的距离为 a. 14分
17、解(Ⅰ)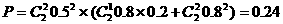 ……6分
……6分
(Ⅱ)两人都得零分的概率为 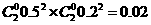
两人都得10分的概率为 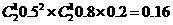
两人都得20分的概率为 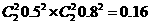
 ∴
∴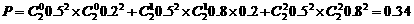 13分
13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com