15．(本小题满分12分)t x

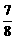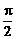已知cos2θ=，θ∈(，π).

(I)求sinθ的值；

(II)求sin (θ+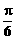)－sin2θ的值.

解：(I)∵ cos2θ=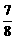，∴ 1－2sin²θ=，

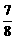∴ sin²θ=.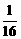

∵θ∈(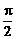，π)，∴ sinθ=.

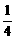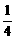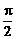(II)∵ sinθ=且θ∈(，π)，

∴ cosθ=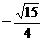，∴ sin2θ= 2sinθcosθ= 2××() =.

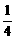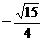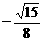∴ sin (θ+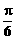)－sin2θ= sinθ·cos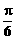+ cosθ·sin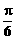－sin2θ

　　　　　　　　　　　　　　　　　 =×+ ()×－()

　　　　　　　　　　　　　　　　　 =.

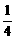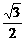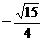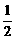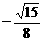14．在密码学中，你直接可以看到的内容为明码，对明码进行某种处理后得到的内容为密码，有一种密码，将英文的26个字母a、b、c，…，z(不论大小写)依次对应1，2，3，…，26，这26个自然数，见表格：

现给出一个变换公式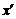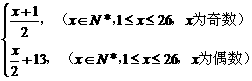：=，可将英文的明文(明码)转换成密码，按上述规定，若将某英文明文译成的密码是shxc，那么原来的明文是　　　　　 .(love)

13．已知m、n是直线，α、β、γ是平面，给出下列命题：① α⊥β，α∩β= m，m⊥n，则n⊥α或n⊥β；② 若α∥β，α∩γ= m，β∩γ= n，则m∥n；③ 如果直线m与平面β内的一条直线平行，那么m∥β；④ 若α∩β= m，n∥m，且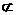nα，n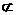β，则n∥α且n∥β. 所有正确命题的序号是　　　　　　 .(②④)

12．在等差数列{a_n}中，已知a₁₁ = 10，那么它的前21项的和S₂₁ = 　　　　　.(210)

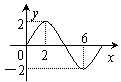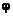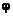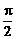
11．函数f (x ) = A sin (ωx +)(A＞0，ω＞0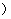，||＜的部分图象如图所示，则f (x )的解析式为　　　　　　 .(f (x ) = 2sin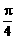x)

10．已知平面向量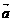= (0，1)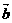，= (x，y)，若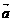⊥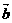，则实数y = 　　　　　.(0)

9．某学校有初中生1080人，高中生900人，教师120人，现对该学校的师生进行样本容量为n的分层抽样，已知抽取的高中生为60人，则样本容量n为　　　　 .(140)

8．4本不同的书全部分给3个同学，每人至少一本，则不同的分法有(　 C )

A．12种　　　　　　 B．24种　　　　　　 C．36种　　　　　　 D．48种

7．若二项式 (x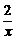－)ⁿ的展开式的第5项是常数项，则正整数n的值为( B　 )

A．7　　　　　 B．8　　　　 C．9　　　　　 D．10

6．如图，四面体P－DEF中，M是棱EF的中点，PD、PE、PF两两垂直，必有( C　 )

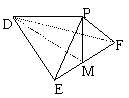A．DM⊥平面PEF

B．PM⊥平面DEF

C．平面PDE⊥平面PEF

D．平面PDE⊥平面DEF