
题目列表(包括答案和解析)
4.在空间中,下列命题中正确的是 ( )
①若两直线a、b分别与直线l平行,则a//b
②若直线a与平面β内的一条直线b平行,则a//β
③若直线a与平面β内的两条直线都垂直,则a⊥β
④若平面β内的一条直线a垂直平面γ,则β⊥γ
A.①②④ B.①④ C.①③④ D.①②③④
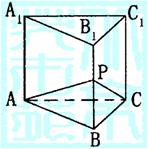 5.如图正三棱柱ABC-A1B1C1底面边长与高相等,截面PAC
5.如图正三棱柱ABC-A1B1C1底面边长与高相等,截面PAC
把棱柱分成两部分的体积之比为5∶1,则二面角P-AC-B
的大小为 ( )
A.30° B.45°
C.60° D.75°
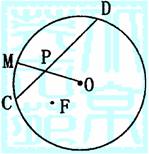 6.如图一圆形纸片的圆心为O,F是圆内一定点,M是圆周
6.如图一圆形纸片的圆心为O,F是圆内一定点,M是圆周
上一动点,把纸片折叠使M与F重合,然后抹平纸片,折
痕为CD,设CD与OM交于P,则点P的轨迹是( )
A.椭圆 B.双曲线
C.抛物线 D.圆
3.已知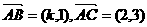 ,则下列k值中能使△ABC是直角三角形的值是 ( )
,则下列k值中能使△ABC是直角三角形的值是 ( )
A.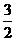 B.
B.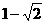 C.
C.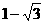 D.-5
D.-5
2.已知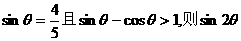 等于 ( )
等于 ( )
A.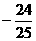 B.
B.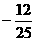 C.
C.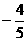 D.
D.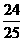
是符合题目要求的.
1.已知集合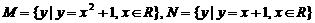 ,那么
,那么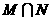 等于( )
等于( )
A.(0,1) B.(0,1),(1,2)C.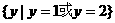 D.
D.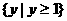
5、已知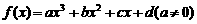 是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数f (x)的图象上是否存在一点M(x0,y0),使得f (x)在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;
(3)求| AC |的取值范围.
(1)解: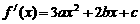
依题意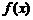 在
在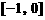 和[0,2]上有相反的单调性,
和[0,2]上有相反的单调性,
∴x = 0是f (x)的一个极值点,故 ,得c = 0
,得c = 0
(2)解:因为f (x)交x轴于点B(2,0)
∴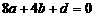 ,即
,即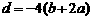
令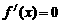 得
得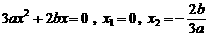
因为f (x)在[0,2]和[4,5]上有相反的单调性,∴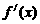 在[0,2]和[4,5]上有相反的
在[0,2]和[4,5]上有相反的
符号
故2≤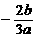 ≤4 Þ -6≤
≤4 Þ -6≤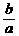 ≤-3
≤-3
假设存在点M(x0,y0)使得f (x)在点M的切线斜率为3b,则f / (x0) =3b,
即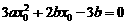

而-6≤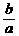 ≤-3,∴△<0
≤-3,∴△<0
故不存在点M(x0,y0),使得f (x)在点M的切线斜率为3b.
(3)解:设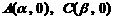 ,依题意可令
,依题意可令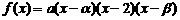
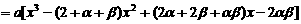
则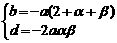 即
即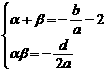
∴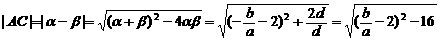
∵-6≤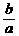 ≤-3,∴当
≤-3,∴当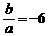 时,
时,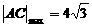 ;
;
当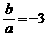 时,
时,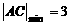 ,故3≤| AC |≤4
,故3≤| AC |≤4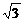
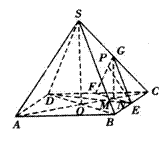
4、在正四棱锥S-ABCD中,E是BC的中点,P点在侧面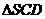 内及其边界上运动,并且总是保持PE
内及其边界上运动,并且总是保持PE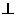 AC.
AC.
(1)指出动点P的轨迹(即说明动点P在满足给定的条件下运动时所形成的图形),证明你的结论;
(2)以轨迹上的动点P为顶点的三棱锥P-CDE的最大体积是正四棱锥S-ABCD体积的几分之几?
(3)设动点P在G点的位置时三棱锥P-CDE的体积取最大值V1,二面角G-DE-C的大小为 ,二面角G-CE-D的大小为
,二面角G-CE-D的大小为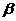 ,求
,求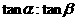 的值.
的值.
 (4)若将“E是BC的中点”改为“E是BC上异于B、C的一定点”,其它条件不变,请指出点P的轨迹,证明你的结论.
(4)若将“E是BC的中点”改为“E是BC上异于B、C的一定点”,其它条件不变,请指出点P的轨迹,证明你的结论.
解析:(1)如图,分别取CD、SC的中点F、G,连结EF、EG、FG、BD.设AC与BD的交点为O,连结SO,则动点P的轨迹是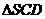 的中位线FG.
的中位线FG.
由正四棱锥可得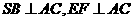 .又
.又
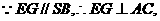
 平面EFG,
平面EFG,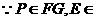 平面EFG,
平面EFG,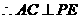 .
.
(2)由于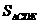 是定值,所以当P到平面CDE的距离最大时,
是定值,所以当P到平面CDE的距离最大时,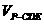 最大,易知当P与G重合时,P到平面CDE的距离最大,故
最大,易知当P与G重合时,P到平面CDE的距离最大,故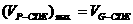 .又
.又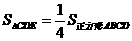 ,G到平面ABCD的距离是点S到平面ABCD的距离的
,G到平面ABCD的距离是点S到平面ABCD的距离的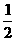 ,
,
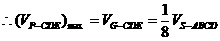 .
.
(3)令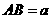 ,EF与AC交于N点,连结GN,则GN
,EF与AC交于N点,连结GN,则GN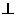 平面ABCD.
平面ABCD.
因此二面角G-DE-C和二面角G-CE-D的平面角的正切值的比就等于N到DE和CE的距离的倒数比.
 N是OC的中点,
N是OC的中点, N到BC的距离为
N到BC的距离为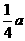 .
.
连结DE交OC于M,则M是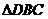 的重心,
的重心,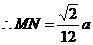 .
.
又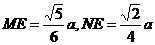 ,
,
在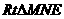 中,容易求得N到DE的距离为
中,容易求得N到DE的距离为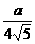 .
.
故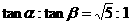 .
.
(4)动点P在侧面SCD内部及其边界上运动,且总保持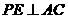 ,那么这些相交于定点E的直线系应位于某个与直线AC垂直的平面内,而由正四棱锥的性质可知,
,那么这些相交于定点E的直线系应位于某个与直线AC垂直的平面内,而由正四棱锥的性质可知,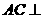 平面SBD,因此动直线PE集中在过E且平行于平面SBD的一个平面内.过E作E
平面SBD,因此动直线PE集中在过E且平行于平面SBD的一个平面内.过E作E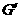 //SB,E
//SB,E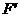 //BD,分别交SC于
//BD,分别交SC于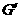 ,交CD于
,交CD于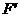 ,则平面E
,则平面E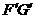 //平面SBD,从而
//平面SBD,从而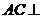 平面E
平面E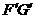 ,故点P的轨迹是线段
,故点P的轨迹是线段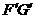 .
.
说明:本题全方位地考查了立体几何中的主要内容,如线面与线线的位置关系、体积问题、二面角问题等.在立体几何的问题中给出了探求点的轨迹问题,与平面几何、解析几何紧密联系,体现了对综合运用知识的能力要求,考查的知识点丰富,具有相当的难度和深度,达到了压轴题的水平,是一道优秀的创新型试题.
3.某一居民小区五幢住宅楼,由于有水紧缺,规定每一幢楼在一周内必须选择某一天停水(选择哪一天是等可能的)。假定每一楼之间的选择互不影响。
(1) 求个5幢楼均选择星期天停水的概率。
(2) 求至少有两幢选择同一天停水的概率。
(1)设5幢楼均选择星期天停水的事件为A,则
P(A)=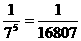 (6`)
(6`)
(2)设五幢楼选择的停电时间各不相同的事件为B,则
P(B)=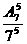 =
=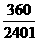 (12`)
(12`)
2、质地均匀的正方体木块的棱长为n,n为正整数且n≥2.在其表面涂上与材质颜色不同的蓝色后将木块分割成棱长为1的小正方体木块,假设从中任意取一块得到表面有蓝色的木块的概率为P,请研究P能否大于或小于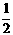 .
.
[解答]:当n=2时, P=1;
当n≥3时,有P=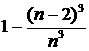 ,
,
P-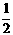 =
=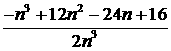 .
.
记y=g(x)=
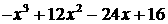 , x>2.
, x>2.
g′(x)=
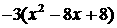 ,
,
可知在(2,+∞)上y= g(x)只有一个极大值点x=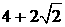 ,
,
所以函数y= g(x)在(2, 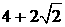 )上是增函数;在(
)上是增函数;在(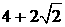 ,+∞)上是减函数.
,+∞)上是减函数.
又验证g(3)>0, g(9) >0, g(10)<0,
于是我们得到结论:当正整数2≤n≤9时, P>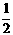 ;当正整数n≥10时, P<
;当正整数n≥10时, P<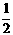 .
.
(2)以双曲线的焦点弦为直径的圆必与其相应的准线相交.
(3)以抛物线的焦点弦为直径的圆必与其相应的准线相切.
(理由):本题亦可出为选择题或解答题中其中一问证明。意在考查圆锥曲线的第二
定义及判定直线与圆的位置关系等相关概念和方法。
(详解):设圆锥曲线过焦点F的弦为AB,过A、B分别向相应的准线作垂线
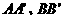 ,则由第二定义得:
,则由第二定义得:

∴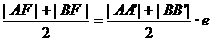
设以AB为直径的圆半径为r,圆心到准线的距离为d,即有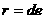
椭圆的离心率 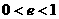 ,此时
,此时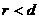 . 相离
. 相离
抛物线的离心率 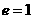 ,此时
,此时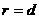 . 相切
. 相切
双曲线的离心率 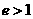 ,此时
,此时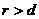 . 相交
. 相交
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com