
题目列表(包括答案和解析)
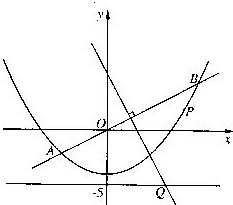
22、(上海)如图, 直线y=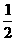 x与抛物线y=
x与抛物线y=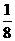 x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
(1) 求点Q的坐标;(2) 当P为抛物线上位于线段AB下方(含A、B) 的动点时, 求ΔOPQ面积的最大值.
21. (上海)圆心在直线x=2上的圆C与y轴交于两点A(0, -4),B(0, -2),则圆C的方程为
.
(上海)圆心在直线x=2上的圆C与y轴交于两点A(0, -4),B(0, -2),则圆C的方程为
.
20.(上海)设抛物线的顶点坐标为(2,0),准线方程为x=-1,则它的焦点坐标为 .
19、(辽宁)设椭圆方程为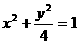 ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足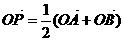 ,点N的坐标为
,点N的坐标为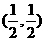 ,当l绕点M旋转时,求: (1)动点P的轨迹方程; (2)
,当l绕点M旋转时,求: (1)动点P的轨迹方程; (2)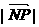 的最小值与最大值.
的最小值与最大值.
18、(辽宁)若经过点P(-1,0)的直线与圆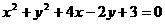 相切,则此直线在y轴上的截距是
.
相切,则此直线在y轴上的截距是
.
17、(辽宁)已知点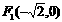 、
、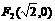 ,动点P满足
,动点P满足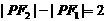 . 当点P的纵坐标是
. 当点P的纵坐标是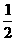 时,点P到坐标原点的距离是
( )
时,点P到坐标原点的距离是
( )
A.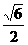 B.
B.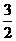 C.
C.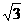 D.2
D.2
16.(江苏)已知椭圆的中心在原点,离心率为,一个焦点是F(-m,0)(m是大于0的常数).
(Ⅰ)求椭圆的方程;
(Ⅱ)设Q是椭圆上的一点,且过点F、Q的直线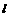 与y轴交于点M. 若
与y轴交于点M. 若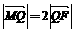 ,求直线
,求直线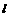 的斜率.
的斜率.
15.(江苏)制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和50﹪,可能的最大亏损率分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
14、(江苏)以点(1,2)为圆心,与直线4x+3y-35=0相切的圆的方程是________________.
13.(江苏)若双曲线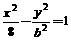 的一条准线与抛物线
的一条准线与抛物线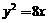 的准线重合,则双曲线的离心率为
( )
的准线重合,则双曲线的离心率为
( )
A.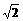 B.
B.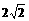 C. 4
D.
C. 4
D.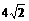
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com