
题目列表(包括答案和解析)
4.某企业生产一种电子产品,2003年的产量在2002年的基础上增长率为a,2004年又在2003年的基础上增长率为b(a,b>0)。若这两年的平均增长率为q,则 ( )
A.q=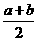 B.q≥
B.q≥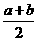 C.q≤
C.q≤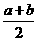 D.大小关系不定
D.大小关系不定
3.从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有 ( )
A.140种 B.120种 C.35种 D.34种
2.某物体一天中的温度T(单位:摄氏度)是时间t(单位:小时)的函数T(t)=t3-3t+60,t=0表示中午12:00,则下午3时的温度为 ( )
A.8℃ B.18℃ C.78℃ D.112℃
1.某村对200户家庭的生活水平进行调查,其中一项的统计结果是:有彩电的180户,有电冰箱的186户,两样都有的168户,则彩电和电冰箱至少有一样的户数是 ( )
A.197 B.198 C.199 D.200
6. 综合性性问题
例18 某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘,根据需要,软件至少买3片,磁盘至少买2盒,则不同的选购方式共有( )
A.5种 B.6种 C.7种 D.8种
讲解 设购买单片软件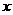 片, 磁盘
片, 磁盘 盒, 由题意得
盒, 由题意得
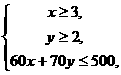
经检验可知,该不等式组的正整数解为:
当 时,
时,
当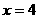 时,
时,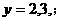
当 时,
时,
总共有7组, 故应选C.
例19 银行计划将某资金给项目M和N投资一年,其中40%的资金给项目M,60%的资金给项目N,项目M能获得10%的年利润,项目N能获得35%的年利润,年终银行必须回笼资金,同时按一定的回扣率支付给储户. 为了使银行年利润不小于给M、N总投资的10%而不大于总投资的15%,则给储户回扣率最小值为( )
A.5% B.10% C.15% D.20%
讲解 设共有资金为 , 储户回扣率
, 储户回扣率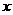 , 由题意得解出
, 由题意得解出
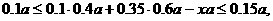
解出 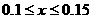 ,故应选B.
,故应选B.
例20 某电视台的颁奖礼盒用如下方法做成:先将一个奖品放入一个正方体内,再将正方体放在一个球内,使正方体内接于球;然后再将该球放入一个正方体内,球内切于该正方体,再将正方体放入一个球内,正方体内接于球,……如此下去,正方体与球交替出现. 如果正方体与球共有13个,最大正方体的棱长为162cm. 奖品为羽毛球拍、蓝球、乒乓球拍、手表、项链之一,则奖品只能是(构成礼品盒材料的厚度忽略不计)( ).
A . 项链 B. 项链或手表
C. 项链或手表,或乒乓球拍 D. 项链或手表,或乒乓球拍,或蓝球
讲解 因正方体的中心与外接球的中心相同,设正方体的棱长为a,外接球的半径为R,则有
 即
即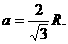
 半径为R的球的外切正方体的棱长
半径为R的球的外切正方体的棱长 ,
,
 相邻两个正方体的棱长之比为
相邻两个正方体的棱长之比为 
因为有7个正方体,设最小正方体的棱长为t,则
 得
得 .
.
故礼品为手表或项链. 故应选B.
高考中的数学选择题一般是容易题或中档题,个别题属于较难题,当中的大多数题的解答可用特殊的方法快速选择. 例如:估值选择法、特值检验法、顺推破解法、数形结合法、特征分析法、逆推验证法、提炼公式法等都是常用的解法. 解题时还应特别注意:数学选择题的四个选择支中有且仅有一个是正确的,因而在求解时对照选支就显得非常重要,它是快速选择、正确作答的基本前提.
5. 解析几何
例14 过抛物线y= x2(a> 0)的焦点F作一直线交抛物线于P、Q两点,若线段FP与FQ的长分别是p、q,则
x2(a> 0)的焦点F作一直线交抛物线于P、Q两点,若线段FP与FQ的长分别是p、q,则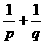 =( ).
=( ).
A. 2a B.  C. 4a D.
C. 4a D. 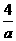
讲解 由题意知,对任意的过抛物线焦点F的直线,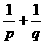 的值都是
的值都是 的表示式,因而取抛物线的通径进行求解,则p=q=
的表示式,因而取抛物线的通径进行求解,则p=q= ,所以
,所以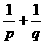 =
=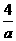 ,故应选D.
,故应选D.
例15 点P 到曲线
到曲线 (其中参数
(其中参数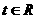 )上的点的最短距离是( ).
)上的点的最短距离是( ).
A. 0
B. 1
C. 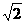 D. 2
D. 2
讲解 由两点间的距离公式,得点P 到曲线上的点Q
到曲线上的点Q 的距离为
的距离为
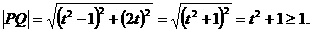
当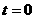 时,
时, 故应选B.
故应选B.
将曲线方程转化为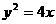 ,显然点P
,显然点P 是抛物线的焦点,由定义可知:抛物线上距离焦点最近的点为抛物线的顶点,故应选B.
是抛物线的焦点,由定义可知:抛物线上距离焦点最近的点为抛物线的顶点,故应选B.
例16 已知椭圆 =1(a>b>0),双曲线
=1(a>b>0),双曲线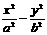 =1和抛物线y2=2px(p>0 )的离心率分别为e1、e2、e3,则( ).
=1和抛物线y2=2px(p>0 )的离心率分别为e1、e2、e3,则( ).
A.e1e2>e3 B.e1e2=e3
C.e1e2<e3 D.e1e2≥e3
讲解 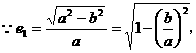


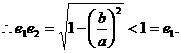
故应选C.
例17 平行移动抛物线 ,使其顶点的横坐标非负,并使其顶点到点
,使其顶点的横坐标非负,并使其顶点到点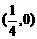 的距离比到y轴的距离多
的距离比到y轴的距离多 ,这样得到的所有抛物线所经过的区域是
,这样得到的所有抛物线所经过的区域是
A. xOy平面 B. 
C.  D.
D. 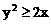
讲解 我们先求出到点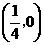 的距离比到y轴的距离多
的距离比到y轴的距离多 的点的轨迹.
的点的轨迹.
设P(x,y)是合条件的点,则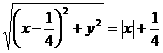 ,
,
两边平方并整理得

再设平移后抛物线的顶点为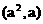 ,于是平移后抛物线的方程为
,于是平移后抛物线的方程为

按a整理得  .
.
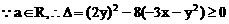 ,化简得
,化简得 .故应选B.
.故应选B.
4. 立体几何
 例12 如图,在多面体ABCDEF中,已知面ABCD是边长为3的
例12 如图,在多面体ABCDEF中,已知面ABCD是边长为3的
正方形,EF∥AB,EF与面AC的距离为2,则该多面体的体积为( )
A. B.5
C.6
D.
B.5
C.6
D.
讲解 本题的图形是非常规的多面体,需要对其进行必要的分割.
连EB、EC,得四棱锥E―ABCD和三棱锥E―BCF,这当中,四棱锥E―ABCD的体积易求得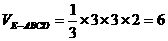 , 又因为一个几何体的体积应大于它的部分体积,所以不必计算三棱锥E―BCF的体积,就可排除A, B.,C.,故应选D.
, 又因为一个几何体的体积应大于它的部分体积,所以不必计算三棱锥E―BCF的体积,就可排除A, B.,C.,故应选D.
“体积变换”是解答立体几何题的常用方法,请予以关注.
例13 关于直线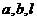 以及平面
以及平面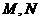 ,下面命题中正确的是( ).
,下面命题中正确的是( ).
A. 若 则
则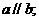
B. 若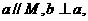 则
则

C. 若 且
且 则
则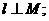
D. 若 则
则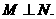
讲解 对于选支D, 过 作平面P交平面N于直线
作平面P交平面N于直线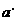 ,则
,则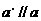 ,而
,而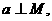 从而
从而
又 故
故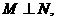 应选D.
应选D.
请读者举反例说明命题A, B, C, 均为假命题.
3. 数列与排列组合
例9
由 给出的数列
给出的数列 的第34项是( ).
的第34项是( ).
A.  B. 100
C.
B. 100
C. 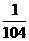 D.
D. 
讲解 对已知递推式两边取倒数, 得
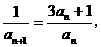
即 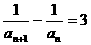 .
.
这说明数列 是以
是以 为首项, 3为公差的等差数列, 从而有
为首项, 3为公差的等差数列, 从而有
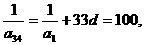
即 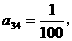 故应选B.
故应选B.
构造等差数列、等比数列是解决数列考题的常用方法, 值得我们重视.
例10 一种细胞,每三分钟分裂一次(一个分裂为两个),把一个这种细胞放入一个容器内,恰好一小时充满;如果开始时把两个这种细胞放入该容器内,那么细胞充满容器的时间为( ).
A. 57分钟 B. 30分钟 C. 27分钟 D.45分钟
讲解 设容器内细胞共分裂n次,则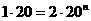 ,即
,即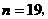 从而共花去时间为
从而共花去时间为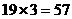 分钟,故应选A.
分钟,故应选A.
例11 从正方形的6个面中选取3个面,其中有2个面不相邻的选法共有( ).
A. 8种 B. 12种 C. 16种 D. 20种
讲解 采用补集思想求解. 从6个面中任取3个面的取法共有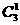 种方法,其中三个面交于一点共有8种可能,从而满足题意的取法共有
种方法,其中三个面交于一点共有8种可能,从而满足题意的取法共有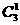
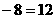 种,故应选B.
种,故应选B.
请读者思考:关系式: 的含义是什么?
的含义是什么?
2. 三角与复数
例5 如果函数y = sin2x + a cos2x的图象关于x=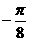 对称,则a=( ).
对称,则a=( ).
A.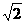 B.-
B.-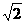 C. 1
D. -1
C. 1
D. -1
讲解 因为点(0,0)与点(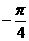 ,0)关于直线x=
,0)关于直线x=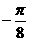 对称,所以a必满足:
对称,所以a必满足:
sin0 + a
cos0=sin( )+ a cos(
)+ a cos( ),
),
解出a=-1,从而可以排除A, B, C.,故应选D.
例6 在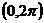 内,使
内,使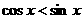 成立的
成立的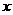 的取值范围是( ).
的取值范围是( ).
A. 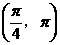 B.
B. 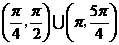
C.  D.
D. 
讲解 将原不等式转化为 由
由 ,知
,知 ,从而
,从而 ,故应选C.
,故应选C.
事实上,由 显然满足
显然满足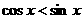 ,从而否定A, B, D, 故应选C.
,从而否定A, B, D, 故应选C.
亦可在同一坐标系中,作出函数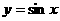 和
和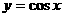 在
在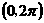 上的图象,进行直观求解.
上的图象,进行直观求解.
例7 复数 在复平面上对应的点不可能位于( ).
在复平面上对应的点不可能位于( ).
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
讲解 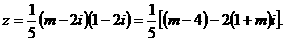
由 无解,可知应选A.
无解,可知应选A.
亦可取特值进行排除.事实上
记复数 对应的点为P.若取
对应的点为P.若取 ,点P在第二象限;若取
,点P在第二象限;若取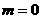 ,则点P在第三象限; 若取
,则点P在第三象限; 若取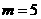 ,则点P在第四象限,故应选A.
,则点P在第四象限,故应选A.
例8 把曲线 先沿
先沿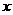 轴向右平移
轴向右平移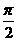 个单位,再沿
个单位,再沿 轴向下平移1个单位,得到的曲线方程是( ).
轴向下平移1个单位,得到的曲线方程是( ).
A.  B.
B. 
C. 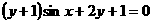 D.
D. 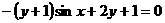
讲解 对 作变换
作变换
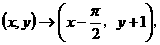
得
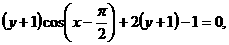
即
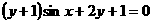 .
.
故应选C.
记住一些运动变换的小结论是有效的.本题是函数 向方程式的变式,较为新颖.
向方程式的变式,较为新颖.
1. 函数与不等式
例1
已知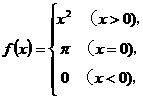 则
则 的值等于( ).
的值等于( ).
A. 0 B. 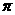 C.
C.  D. 9
D. 9
讲解 由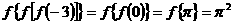 ,可知选C.
,可知选C.
例2 函数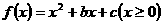 是单调函数的充要条件是( ).
是单调函数的充要条件是( ).
A.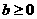 B.
B.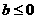 C.
C. 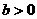 D.
D. 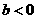
讲解 抛物线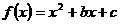 的开口向上,其对称轴为
的开口向上,其对称轴为 ,于是有
,于是有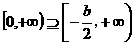 是递增区间,从而
是递增区间,从而 即
即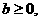 应选A.
应选A.
例3 不等式 的解集是( ).
的解集是( ).
A.  B.
B.  C.
C. 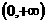 D.
D. 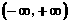
讲解 当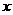 与
与 异号时,有
异号时,有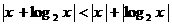 , 则必有
, 则必有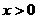 ,从而
,从而 ,解出
,解出 ,故应选A.
,故应选A.
例4
关于函数 ,有下面四个结论:
,有下面四个结论:
(1) 是奇函数;
是奇函数;
(2)当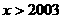 时,
时,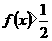 恒成立;
恒成立;
(3)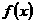 的最大值是
的最大值是 ;
;
(4) 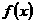 的最小值是
的最小值是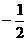 .
.
其中正确结论的个数是( ).
A. 1个 B. 2个 C. 3个 D. 4个
讲解 由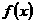 是偶函数,可知(1)错;
是偶函数,可知(1)错;
又当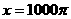 时,
时, ,所以错(2);
,所以错(2);
当 ,故(3)错;
,故(3)错;
从而对照选支应选A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com