
题目列表(包括答案和解析)
8.已知实数x、y满足x2+y2=1,则(1-xy)(1+xy)( )
A.有最小值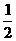 ,也有最大值1 B.有最小值
,也有最大值1 B.有最小值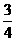 ,也有最大值1
,也有最大值1
C.有最小值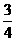 ,但无最大值 D.有最大值1,但无最小值
,但无最大值 D.有最大值1,但无最小值
7.若a、b、c、d满足条件:c<d且a+d<b+c和a+b=c+d,则下列不等式中正确的是( )
A.a<c<b<d B.b<c<d<a C.c<a<b<d D.a<c<d<b
6.x为实数,且|x-3|-|x-1|>m恒成立,则m的取值范围是( )
A.m>2 B.m<2 C.m>-2 D.m<-2
5.已知a2+b2+c2=1,那么下列不等式中成立的是( )
A.(a+b+c) 2≥1 B.ab+bc+ca≥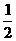
C.|abc|≤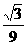 D.ab2>ab>a
D.ab2>ab>a
4.若a<0,-1<b<0,下面结论正确的是( )
A.a>ab>ab2 B.ab>ab2>a Cab>a>ab2 D.ab2>ab>a
3.a,b∈R且a>b,则下列不等式中恒成立的是( )
A.a2>b2 B.( 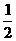 )
a <(
)
a <(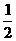 )b C.lg(a-b)>0 D.
)b C.lg(a-b)>0 D.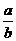 >1
>1
2.若a3<-5,则下列关系式中正确的是( )
A.a4>-5a
B.a2<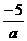 C.a6<25 D.a>
C.a6<25 D.a>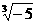
1.“x>y且m>n”是“x+m>y+n”成立的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.不充分不必要条件
2.证明不等式的常用方法
除了课本介绍了证明不等式的三种基本方法外,还有如下常用方法:
(1)放缩法
若证明“A≥B”,我们先证明“A≥C”,然后再证明“C≥B”,则“A≥B”。
(2)反证法
反证法是通过否定结论导致矛盾,从而肯定原结论正确的一种方法。
(3)数学归纳法
证明与自然数n有关的不等式时,常用数学归纳法。此法高考中已多次考查。
(4)变量代换法
变量代换是数学中一种常用的解题方法,对于一些结构比较复杂,变化较多而关系不太清楚的不等式,可适当地引进一些新的变量进行代换,以简化其结构,其代换技巧有局部代换、整体代换、三角代换、增量代换等。
(5)函数方法
通过利用函数的性质,如单调性、凸性、有界性、实根存在的条件证明不等式的方法称为函数方法。
(6)构造方法
不等式证明中的构造方法,主要是指通过引进合适的恒等式、数列、函数,图形及变量代换等辅助手段,促使命题转化,从而使不等式得证。此法技巧要求较高,高考试题中很少见。
例题解析
[例1] 证明下列不等式:
(1)若x,y,z∈R,a,b,c∈{x|x是正实数集},则
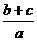 x2+
x2+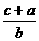 y2+
y2+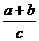 z2≥2(xy+yz+zx)
z2≥2(xy+yz+zx)
(2)若x,y,z∈{x|x是正实数集},且x+y+z=xyz,则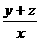 +
+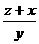 +
+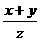 ≥2(
≥2(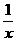 +
+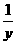 +
+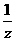 )2
)2
[解] (1)先考虑用作差证法
∵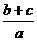 x2+
x2+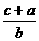 y2+
y2+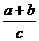 z2-2(xy+yz+zx)=
(
z2-2(xy+yz+zx)=
(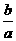 x2+
x2+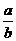 y2-2xy)+(
y2-2xy)+(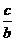 y2+
y2+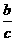 z2-2yz)+
z2-2yz)+
(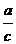 z2+
z2+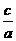 x2-2zx)=(
x2-2zx)=(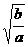 x
x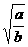 y)2+(
y)2+(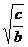 y-
y-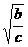 z)2+(
z)2+(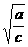 z-
z-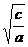 x)2≥0
x)2≥0
∴
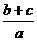 x2+
x2+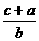 y2+
y2+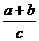 z2≥2(xy+yz+zx)
z2≥2(xy+yz+zx)
(2)采用等价转化法
所证不等式等价于
x2y2z2(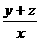 +
+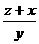 +
+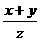 )≥2(xy+yz+zx)2
)≥2(xy+yz+zx)2
 xyz·[yz(y+z)+zx(z+x)+xy(x+y)]≥2(xy+yz+zx)2
xyz·[yz(y+z)+zx(z+x)+xy(x+y)]≥2(xy+yz+zx)2
 (x+y+z)(y2z+yz2+z2x+zx2+x2y+xy2)≥2(x2y2+y2z2+z2x2)+4(x2yz+xy2z+xyz2)
(x+y+z)(y2z+yz2+z2x+zx2+x2y+xy2)≥2(x2y2+y2z2+z2x2)+4(x2yz+xy2z+xyz2)
 y3z+yz3+z3x+zx3+x3y+xy3≥zx2yz+2xy2z+2xyz2
y3z+yz3+z3x+zx3+x3y+xy3≥zx2yz+2xy2z+2xyz2
 yz(y-z) 2 +zx(z-x) 2+xy(x-y)
2+x2 (y-z) 2+y2 (z-x)+z2
(x-y) 2≥0
yz(y-z) 2 +zx(z-x) 2+xy(x-y)
2+x2 (y-z) 2+y2 (z-x)+z2
(x-y) 2≥0
∵上式显然成立 ∴原不等式得证。
[注] (1)配方技巧的实现关键在于合理的分项,正是这种分项我们对(1)还可证明如下:
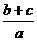 x2+
x2+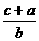 y2+
y2+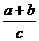 z2
z2
=(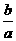 x2+
x2+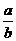 y2)+(
y2)+(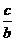 y2+
y2+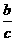 x2)+(
x2)+(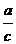 z2+
z2+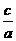 x2)
x2)
≥2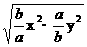 +2
+2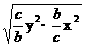 +2
+2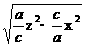
≥2(xy+yz+zx)
(2)的证法要害是:化分式为整式,活用条件,即用x+y+z代换xyz,以及配方技术。事实上,这个代数不等式的实质是如下三角不等式:
在锐角△ABC中,求证:
cotA(tanB+tanC)+cotB·(tanC+tanA)+cotC·(tanA+tanB)≥2(cotA+cotB+cotC)2
[例2] x,y,z∈R,且x+y+z=1,x2+y2+z2=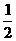 ,则x,y,z,∈[0,
,则x,y,z,∈[0,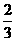 ]
]
[证法一]由x+y+z=1,x2+y2+z2=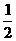 ,得:x2+y2+(1-x-y)2=
,得:x2+y2+(1-x-y)2=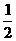
整理成关于y的一元二次方程得:
2y2-2(1-x)y+2x2-2x+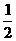 =0
=0
∵y∈R,故Δ≥0。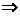
4(1-x)2-4×2(2x2-2x+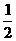 )≥0
)≥0
解之得:0≤x≤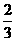 ∴x∈[0,
∴x∈[0,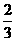 ]
]
同理可得:y,z∈[0,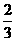 ]
]
[证法二] 设x=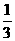 +x′,y=
+x′,y=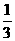 +y′,z=
+y′,z=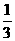 +z′,则x′+y′+z′=0
+z′,则x′+y′+z′=0
于是
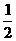 =(
=(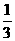 +x′)2+(
+x′)2+(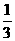 +y′)2+(
+y′)2+(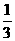 +z′)2
+z′)2
=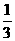 +x′2+y′2+z′2+
+x′2+y′2+z′2+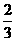 (x′+y′+z′)
(x′+y′+z′)
=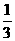 +x′2+y′2+z′2
+x′2+y′2+z′2
≥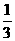 +x′2+
+x′2+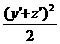
=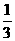 +
+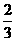 x′2
x′2
故x′2≥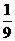 ,x′∈[-
,x′∈[-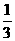 ,
,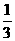 ],x∈[0,
],x∈[0, 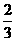 ]同理,y,z∈[0,
]同理,y,z∈[0, 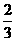 ]
]
[证法三]反证法
设x、y、z三数中若有负数,不妨设x<0,则x2>0,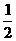 =x2+y2+z2≥x2+
=x2+y2+z2≥x2+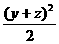 =
=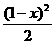 +x2=
+x2=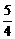 x2-x+
x2-x+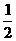 >
>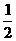 矛盾。
矛盾。
x,y,z,三数中若有最大者大于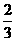 ,不妨设x>
,不妨设x>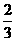 ,则:
,则:
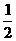 =x2+y2+z2≥x2+
=x2+y2+z2≥x2+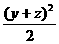
=x2+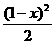 =
=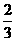 x2-x+
x2-x+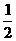
=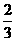 x·(x-
x·(x-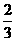 )+
)+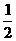 >
>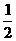 ,矛盾。
,矛盾。
故x,y,z∈[0, 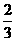 ]。
]。
[注]本题证法甚多,最易接受的方法是证法一的判别式法。因为该法思路明晰,易于操作。技巧性不强。
[例3]已知i、m、n是正整数,且1<i≤m<n。
(1)证明:niAmi<miAni;
(2)证明:(1+m)n>(1+n)m。
[证明] (1)对于1<i≤m,且Ami=m……(m-i+1),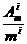 =
=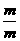 ·
·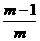 ……
……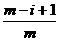 ,
,
同理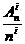 =
= ·
·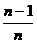 ……
……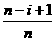
由于m<n,对于整数k=1,2,…,i-1,有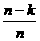 >
>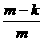 ,所以
,所以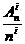 >
>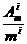
即 miAni>niAmi
(2)由二项式定理有
(1+m)n=1+Cn1m+Cn2m2+…+Cnnmn
(1+n)m=1+Cm1n+Cm2n2+…+Cmmnn
由(1)知miAni>niAmi (1<i≤n)
而Cmi=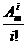 ,
Cni=
,
Cni=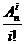 ,
,
∴miCni>niCmi (1<m<n)
∴m0Cn0= n0Cn0=1, mCn1= nCm1=m·n, m2Cn2> n0Cm0,…mmCnm> nmCmm, mm+1Cnm+1 >0,…, mmCnn >0,
∴1+ Cn1m + Cn2m2+…+ Cnnmn >1+ Cm1n+ Cm2n2 +…+ Cmmnn。即
(1+m)n>(1+n)m成立。
[注] 本题是2001年全国高考数学试题,上述证明方法关键是配对。除了上述证法外,本题还有许多另外的证法,下面另举两种证法。
(1)法一:令n=m+k,k∈N
对自然数k=1,2,…,i-1,t<m,有
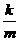 <
<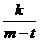 ,从而得:1+
,从而得:1+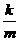 <1+
<1+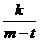
∴(1+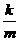 )i<(1+
)i<(1+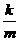 )(1+
)(1+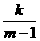 )…(1+
)…(1+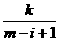 )
)
∴(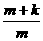 )i<
)i<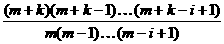
∴(m+k)im(m-1)…(m-i+1)<mi(m+k)(m+k+1)…(m+k-i+1)即
niAmi<miAnI
法二:因为i、m、n是正整数,且1<i≤m<n,不妨设n=m+k(其中k∈N)。下面对正整数i实施数学归纳法。
(i)当i=2时,左边=n2Am2=n2m(m-1)=n2
(m2-m)=(m+k) 2 (m2-m)=m2·(m+k) 2-m·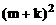 ,右边=m2An2=m2n(n-1)=m2
(m+k)(m+k-1)=m2 (m+k) 2-m2 (m+k)
,右边=m2An2=m2n(n-1)=m2
(m+k)(m+k-1)=m2 (m+k) 2-m2 (m+k)
∵(m+k) 2>m·(m+k) ∴m(m+k) 2<m2 (m+k)
故m2 (m+k) 2-m(m+k) 2<m2 (m+k) 2-m2 (m+k),即左边<右边,这说明i=2时,原不等式成立。
(ii)假设i=l时,nlAml<ml·Anl(1<l≤m<n)成立。∵n(m-l)<m·(n-l)
∴nl+1Aml·(m-l)<ml+1·Anl·(n-l)
∴nl+1Aml+1<ml+1·Anl+1(1<l+1≤m<n)
这说明i=l+1时,也成立。
由(i)(ii)可知,对于满足条件1<i≤m的所有自然数i,原不等式成立。
(2)法一:令f(k)=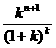 (k≥3,k∈N)
(k≥3,k∈N)
∵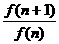 =
=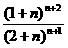 ·
·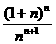
=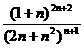 =
=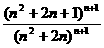 >1
>1
∴f(n+1)>f(n)
∴当k≥3,k∈N时,f(k)单调递增。
∴kk+1>(k+1)k,即k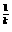 >(k+1)
>(k+1)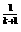
于是经过有限次传递,必有:
(n+1) 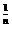 >(m+1)
>(m+1)
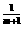
∴(1+m)n>(1+n)m
法二:(1+m)n>(1+n)m nlg(1+m)>mlg(1+n)
nlg(1+m)>mlg(1+n)

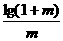 >
>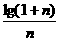
令f(n)= 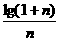 ,n≥2
,n≥2
又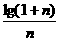 >
>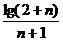
 (1+n)n+1>(2+n)n
(1+n)n+1>(2+n)n
 (
(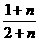 )n>
)n>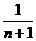
 (1-
(1-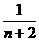 )n>
)n>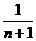
∵n≥2,- 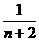 >-1
>-1
∴由贝努利不等式得(1-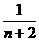 )n>1-
)n>1-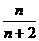 =
=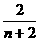 >
>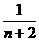
∴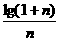 >
>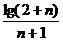 递减,又m<n
递减,又m<n
∴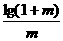 >
>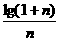
∴(1+m)n>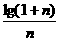
[例4]解下列关于x的不等式:
(1)a2x+1≤ax+2+ax-2(a>0);
(2)loga(1-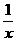 )>1(a>0且a≠1)。
)>1(a>0且a≠1)。
[解]在解指、对数不等式时,常要对底数a进行分类,然后依据其函数的单调性来实现转化,在转化过程中注意不等式解的等价性。
(1)原不等式等价于
a2x-(a2+a-2)ax+1≤0
 (ax-a2)(ax-a-2)
≤0
(ax-a2)(ax-a-2)
≤0
(i)当0<a<1时,a2<a-2,∴a2≤ax≤a-2
即-2≤x≤2
(ii)当a>1时,a2>a-2,∴a-2≤ax≤a2
即-2≤x≤2
(iii)当a=1时,x为一切实数。
综上所述:当0<a<1,原不等式的解为{x|-2≤x≤2};当a=1时,解集为 R。
(2)(i)当a>1时,原不等式等价于
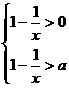
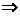 1-
1-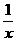 >a
>a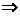 1-a>
1-a>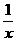
∵1-a<0 ∴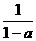 <x<0
<x<0
(ii)当0<a<1时,原不等式等价于
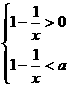
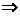
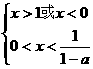
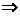 1<x<
1<x<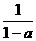
综上所述:当a>1时,原不等式解集是{x|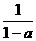 <x<0};当0<a<1时,原不等式的解集是{x|1<x<
<x<0};当0<a<1时,原不等式的解集是{x|1<x<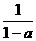 }。
}。
[注] (1)本题求解过程中易漏掉a=1的情形,希望同学们加以注意。
(2)如果应用性质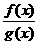 <0
<0 f(x)·g(x)<0,就能简化上述解法。事实上
f(x)·g(x)<0,就能简化上述解法。事实上
(i)当a>1时,原不等式等价于
1-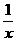 >a
>a
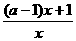 <0
<0
 x(x-
x(x-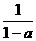 )<0
)<0
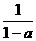 <x<0
<x<0
(ii)当0<a<1时,原不等式等价于
0<1-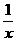 <a
<a (1-
(1-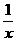 )(1-
)(1-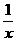 -a)<0
-a)<0

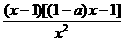 <0
<0
 (x-1)(x-
(x-1)(x-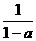 )<0
)<0
 1<x<
1<x<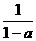
记住一些有用的小结论,有利于优化解题过程。
[例5] 设函数f(x)=logb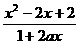 (b>0且b≠1)。
(b>0且b≠1)。
(1)求f(x)的定义域;
(2)当b>1时,求使f(x)>0的所有x的值。
[解] (1)∵x2-2x+2恒正,
∴f(x)的定义域是1+2ax>0。
即当a=0时,f(x)定义域是全体实数。
当a>0时,f(x)的定义域是(-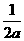 ,+∞)
,+∞)
当a<0时,f(x)的定义域是(-∞,+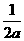 )
)
(2)当b>1时,在f(x)的定义域内,f(x)>0
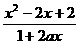 >1
>1 x2-2x+2>1+2ax
x2-2x+2>1+2ax
 x2-2(1+a)x+1>0
x2-2(1+a)x+1>0
其判别式Δ=4(1+a)2-4=4a(a+2)
(i)当Δ<0时,即-2<a<0
∵x2-2(1+a)x+1>0
∴f(x)>0 x<-
x<-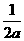
(ii)当Δ=0时,即a=-2或0
若a=0,f(x)>0 (x-1)2>0
(x-1)2>0
 x∈R且x≠1
x∈R且x≠1
若a=-2,f(x)>0 (x+1)2>0
(x+1)2>0
 x<
x<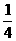 且x≠-1
且x≠-1
(iii)当△>0时,即a>0或a<-2
方程x2-2(1+a)x+1=0的两根为
x1=1+a-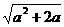 ,x2=1+a+
,x2=1+a+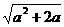
若a>0,则x2>x1>0>-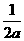
f(x)>0 x<1+a-
x<1+a-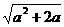 或1+a+
或1+a+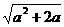 <x<-
<x<-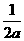
综上所述:当-2<a<0时,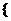 x|x<-
x|x<-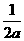
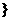
当a=0时,R,
当a=-2时: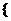 x|x<-1或-1<x<
x|x<-1或-1<x<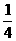
当a>0时,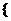 x|x>1+a+
x|x>1+a+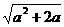 或-
或-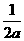 <x<1+a-
<x<1+a-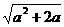
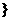
当a<-2时,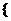 x|x<1+a-
x|x<1+a-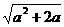 或1+a+
或1+a+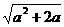 <x<-
<x<-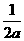
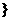
[注] 解题时要注意函数的定义域。
[例6] 解不等式
(1)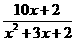 ≥x+1;
≥x+1;
(2)|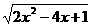 -x|<1的解集。
-x|<1的解集。
[解] (1)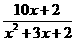 ≥x+1
≥x+1

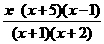 ≤0
≤0
 x·(x-1)(x+1)(x+2)(x+5)≤0,且x≠-1,-2,由图可知,原不等式的解集为:
x·(x-1)(x+1)(x+2)(x+5)≤0,且x≠-1,-2,由图可知,原不等式的解集为:
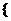 x|x≤-5或-2<x<-1或0≤x≤1
x|x≤-5或-2<x<-1或0≤x≤1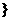
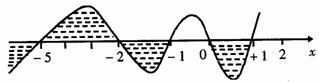
(2)|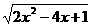 -x|<1
-x|<1
 x-1<
x-1<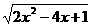 <x+1
<x+1
而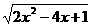 <x+1
<x+1
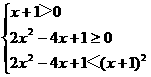 解之得:
解之得: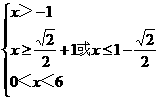
所以,0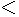 x≤1-
x≤1-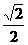 或1+
或1+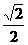 ≤x
≤x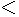 6
6
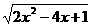 >x-1
>x-1
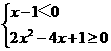 或
或 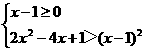
解之得:x≤1-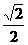 或x>2
或x>2
所以原不等式的解集为 0,1-
0,1-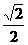
 (2,6)
(2,6)
[注] (1)解高次不等式时常采用数轴标根法,其做法是:先将每个因式分别等于零的根标在数轴上,然后按由上而下,由右向左的次序画图穿过各个零点,选出符合条件的区间。如有重因式,特别注意重因式的零点。如:(x-a)2n·f(x)≥0 f(x)≥0或x=a,(x-a)2n·f(x) >0
f(x)≥0或x=a,(x-a)2n·f(x) >0 f(x)>0且x≠a;(x-a)2n-1·f(x)≥0
f(x)>0且x≠a;(x-a)2n-1·f(x)≥0 (x-a)f(x)≥0。
(x-a)f(x)≥0。
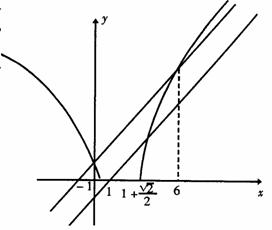
(2)本题的第(2)小题的几何解释是:在同一个坐标系中分别作出函数y=x-1,y=x+1和y=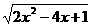 的图像。于是,不等式x-1<
的图像。于是,不等式x-1<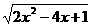 <x+1的解集就是使函数y=
<x+1的解集就是使函数y=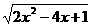 的图像(双曲线2(x-1)2-y2=1,位于x轴上方的部分)夹在直线y=x-1与y=x+1之间的x集合(如图)。
的图像(双曲线2(x-1)2-y2=1,位于x轴上方的部分)夹在直线y=x-1与y=x+1之间的x集合(如图)。
[例7] 已知当x∈[0,1]时,不等式
x2cos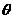 -x·(1-x)+(1-x)2sin
-x·(1-x)+(1-x)2sin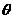 >0
>0
恒成立,试求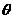 的取值范围。
的取值范围。
[解] 令f(x)=x2cos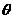 -x·(1-x)+(1-x)2sin
-x·(1-x)+(1-x)2sin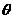 ,对x∈[0,1],f(x)>0恒成立。
,对x∈[0,1],f(x)>0恒成立。
∴cos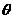 =f(1)>0,sin
=f(1)>0,sin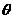 =f(0)>0 (1)
=f(0)>0 (1)
f(x)=(1+cos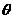 +sin
+sin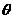 )x2-(1+2sin
)x2-(1+2sin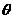 )x+sin
)x+sin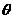
其对称轴,x=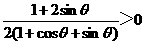 ,且小于1。
,且小于1。
所以:(1+2xin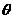 )2-4·(1+cos
)2-4·(1+cos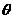 +sin
+sin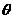 )·sin
)·sin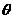 <0 (2)
<0 (2)
反之(1)、(2)成立,f(x)>0 x∈[0,1]恒成立。
故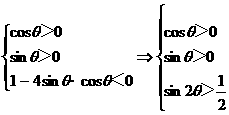
解之得:2kπ+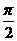 <
<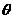 <2kπ+
<2kπ+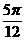 ,k∈Z。
,k∈Z。
[注] 二次函数的在区间上最大值、最小值,只要考虑两个端点处及区间中对称轴所在的位置之点。
[例8] 设函数f(x)=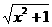 -ax
-ax
(1)解不等式f(x)≤1
(2)求a的取值范围,使函数f(x)在区间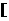 0,+∞
0,+∞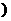 上是单调函数。
上是单调函数。
[解] (1)不等式f(x)≤1即
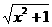 ≤1+ax
≤1+ax
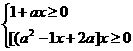
所以:(i)当0<a<1,所给不等式的解集是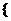 x|0≤x≤
x|0≤x≤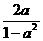
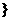
(ii)a≥1时,所给不等式的解集是{x|x≥0}
(iii)当a=0时,所给不等式的解集是{0}
(iv)当-1<a<0时,所给不等式的解集是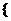 x|
x|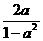 ≤x≤0
≤x≤0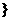
(v)当a≤-1时,所给不等式的解集是{x|x≤0}
(2)在区间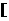 0,+∞
0,+∞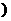 上任取x1,x2,使得x1<x2
上任取x1,x2,使得x1<x2
f(x1)-f(x2)=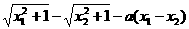
=(x1-x2)(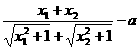 )
)
而f(x)在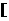 0,+∞
0,+∞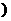 上单调
上单调
∴f(x1)-f(x2)在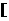 0,+∞
0,+∞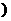 上恒正或恒负。
上恒正或恒负。
又∵x2-x1>0,x1·x2∈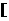 0,+∞
0,+∞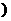
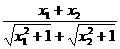 ∈(0,1)
∈(0,1)
∴a≥1或a≤0
[例9] 设函数f(x)=ax2+8x+3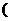 a<0
a<0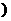 。对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5都成立。
。对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5都成立。
问:a为何值时l(a)最大?求出这个最大的l(a),证明你的结论。
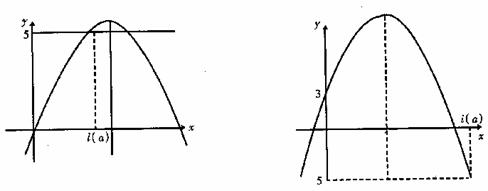
[解] f(x)=a·(x+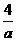 )2+3-
)2+3-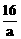 ∵a<0,所以f(x)max=3-
∵a<0,所以f(x)max=3-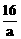
(i)当3-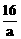 >5,即-8<a<0,此时0<l(a)<-
>5,即-8<a<0,此时0<l(a)<-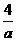
所以,l(a)是方程
ax2+8x+3=-5的较小根。
l(a)=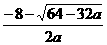
=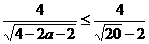 =
=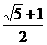
当且仅当a=-8时,等号成立。
由于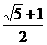 >
>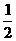 ,因此当且仅当a=-8时,l(a)取最大值
,因此当且仅当a=-8时,l(a)取最大值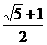 。
。
[注] 本题是一个典型的函数、方程、不等式的综合题。数形结合利于开拓思路,找到解法。
[例10] 设{an}是由正数组成的等比数例,Sn是其前n项和,
(1)证明: <lgSn+1;
<lgSn+1;
(2)是否存在常数C>0,使得
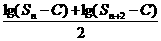 =lg(Sn+1-C)
=lg(Sn+1-C)
成立?证明你的结论。
[解] (1)∵{an}是由正数组成的等比数列。
∴a1>0,q>0
当q=1时,Sn=na1,Sn+2=(n+2)a1
Sn+1=(n+1)a2
Sn·Sn+2=na1·(n+2)a1=n2a12+2na12<n2a12+2na12+a12=[(n+1)a1]2=S2n+1
∴S n·Sn+2<S2n+1
当q≠1时
Sn=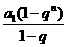 Sn+2=
Sn+2=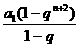 Sn+1=
Sn+1=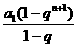
S n·Sn+2=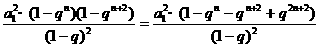
S2n+1=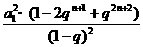
于是,S2n+1-Sn·Sn+2=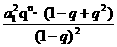 =a12·qn>0
=a12·qn>0
综上所述:S2n+1>Sn·Sn+2

 <lgSn+1
<lgSn+1
(2)证法一:
(1)当q=1时
(Sn-C)(Sn+2-C)-(Sn+1-C)2
=(na1-C)[(n+2)a1-C]-[(n+1)a1-C]2=-a12<0故这样的C>0不存在。
(2)当q≠1时
(Sn-C)(Sn+2-C)-(Sn+1-C)2
=-a1qn·[a1-C(1-q)]
∵a1>0,q>0,a1·qn≠0 ∴C=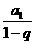
∵C>0,∴0<q<1,但0<q<1时,an-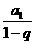 <0,这与条件(2)矛盾,故这样的C>0不存在。
<0,这与条件(2)矛盾,故这样的C>0不存在。
证法二:(反证法)假设存在常数C>0,使得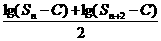 =lg(Sn+1-C)成立,则必有
=lg(Sn+1-C)成立,则必有
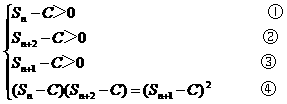
由④式得:
Sn·Sn+2-S2n+1=C·(Sn+Sn+2-2Sn+1)
另一方面:
Sn+Sn+2-2Sn+1=(Sn-C)+(Sn+2-C)-2(Sn+1-C)≥2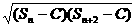 -2(Sn+1-C)=0
-2(Sn+1-C)=0
∴Sn·Sn+2≥Sn+12矛盾
故这样的C>0不存在。
[注]本题是一道数列、不等式、函数的综合性题。解题过程中特别要注意q=1与q≠1的讨论。
(2)中的反证法,综合体现了不等式知识的灵活实用,具有较高的能力要求。
跟踪练习
1.不等式中常见的基本思想方法
(1)等价转化。具体地说,就是无理化为有理,分式化为整式,高次化为低次,绝对值化为非绝对值,指数、对数化为代数式等。
(2)分类讨论。分类讨论的目的是处理问题解决过程中遇到的障碍,在无障碍时不要提前进行分类讨论。
(3)数形结合。有些不等式的解决可能化为两个函数图像间的位置关系或几何问题。
(4)函数方程思想。解不等式可化为解方程及函数图像与x轴交点问题,然后根据题意判断所求解的区间。如“标根法”实际上是一种函数、方程思想。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com