
题目列表(包括答案和解析)
4.已知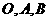 是平面上的三点,直线
是平面上的三点,直线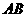 上有一点
上有一点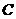 ,满足
,满足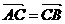 ,则
,则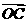 等于 ( )
等于 ( )
A. 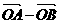 B.
B. 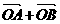 C.
C. 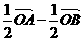 D.
D. 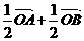
3.若平面向量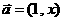 和
和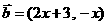 互相平行,其中
互相平行,其中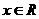 .则
.则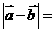 ( )
( )
A.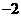 或0;
B.
或0;
B. 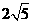 ;
C.2或
;
C.2或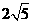 ; D.
; D.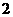 或
或 .
.
2.设向量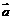 =(-2,1),
=(-2,1),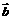 =(λ,-1) (λ∈R),若
=(λ,-1) (λ∈R),若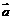 、
、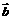 的夹角为钝角,则λ的取值范围是( )
的夹角为钝角,则λ的取值范围是( )
A.(-∞, 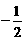 ) B. (
) B. (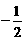 , +∞) C.(
, +∞) C.(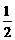 , +∞) D. (-
, +∞) D. (-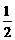 , 2)∪(2, +∞)
, 2)∪(2, +∞)
1.已知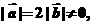 且关于
且关于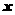 的方程
的方程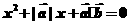 有实数根,则
有实数根,则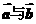 的夹角的取值范围是
( )
的夹角的取值范围是
( )
A.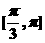 B.
B.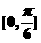 C.
C.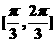 D.
D.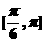
6.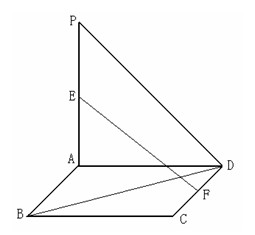 (本小题满分14分)如图,平面
(本小题满分14分)如图,平面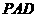 ⊥平面
⊥平面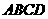 ,
,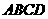 为正方形,
为正方形,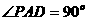 ,且
,且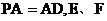 分别是线段
分别是线段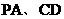 的中点.
的中点.
(Ⅰ)求证: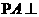 平面
平面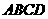 ;
;
(Ⅱ)求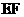 和平面
和平面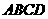 所成的角
所成的角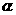 ;
;
(Ⅲ)求异面直线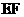 与
与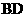 所成的角
所成的角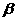 .
.
5.(本题满分15分,第1小题7分,第2小题8分)
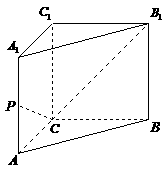 如图,在直三棱柱
如图,在直三棱柱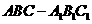 中,
中,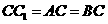 ,
,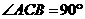 ,
,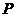 是
是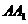 的中点,
的中点,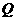 是
是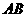 的中点.
的中点.
(1)求异面直线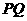 与
与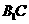 所成角的大小;
所成角的大小;
(2)若直三棱柱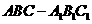 的体积为
的体积为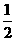 ,求四棱锥
,求四棱锥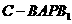 的体积.
的体积.
4.(本题满分15分,第1小题6分,第2小题9分)
如图,在直三棱柱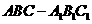 中,
中,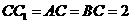 ,
,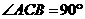 .
.
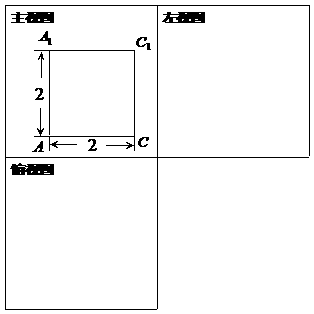
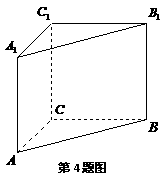 (1) 下图给出了该直三棱柱三视图中的主视图,请据此画出它的左视图和俯视图;
(1) 下图给出了该直三棱柱三视图中的主视图,请据此画出它的左视图和俯视图;
(2) 若 是
是 的中点,求四棱锥
的中点,求四棱锥 的体积.
的体积.
3.(本题满分16分)第1小题满分6分,第2小题满分10分.
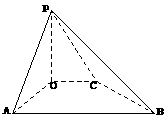
已知四边形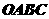 为直角梯形,
为直角梯形,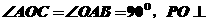 平面
平面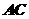 ,且
,且
(理)若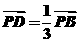 ,求:(1)点
,求:(1)点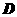 的坐标;
的坐标;
(2)异面直线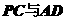 所成的角
所成的角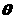 (用反三角函数值表示).
(用反三角函数值表示).
(文)(1)求证: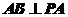 ;(2)求异面直线
;(2)求异面直线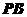 与
与 所成的角
所成的角 (用反三角函数值表示).
(用反三角函数值表示).
2.(本题满分14分)第1小题8分,第2小题6分.
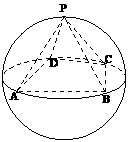 如图,正四棱锥
如图,正四棱锥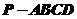 底面的四个顶点
底面的四个顶点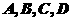 在球
在球 的同一个大圆上,点
的同一个大圆上,点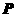 在球面上,且已知
在球面上,且已知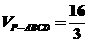 .
.
(1)求球 的表面积;
的表面积;
(2)设 为
为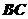 中点,求异面直线
中点,求异面直线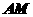 与
与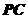 所成角的大小.
所成角的大小.
1.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图,在四棱锥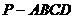 中,底面
中,底面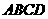 是边长为
是边长为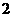 的菱形,
的菱形,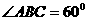 ,
,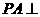 平面
平面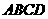 ,
,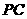 与平面
与平面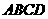 所成角的大小为
所成角的大小为 ,
,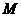 为
为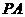 的中点.
的中点.
(1)求四棱锥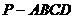 的体积;
的体积;
(2)求异面直线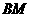 与
与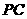 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com