6．三个元件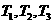正常工作的概率分别为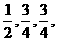将它们中某两个元件并联后再和第三元件串联接入电路.

(Ⅰ)在如图的电路中，电路不发生故障的概率是多少？

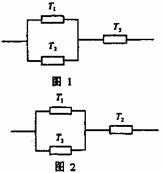
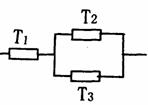　 (Ⅱ)三个元件连成怎样的电路，才能使电路中不发生故障的概率最大？请画出此时电路图，并说明理由.

解：记“三个元件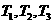正常工作”分别为事件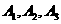，则

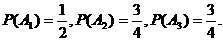
(Ⅰ)不发生故障的事件为.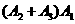

∴不发生故障的概率为

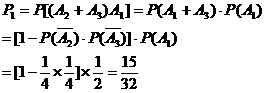
(Ⅱ)如图，此时不发生故障的概率最大.证明如下：

图1中发生故障事件为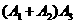

∴不发生故障概率为

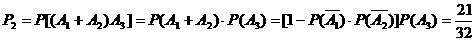
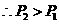
图2不发生故障事件为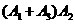，同理不发生故障概率为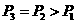

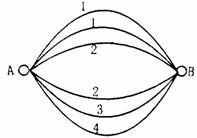
5．如图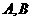，两点之间有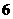条网线并联，它们能通过的最大信息量分别为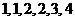.现从中任取三条网线且使每条网线通过最大的信息量.

　 　 (I)设选取的三条网线由到可通过的信息总量为，当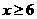时，则保证信息畅通.求线路信息畅通的概率；

　 (II)求选取的三条网线可通过信息总量的数学期望.

解：(I)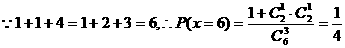

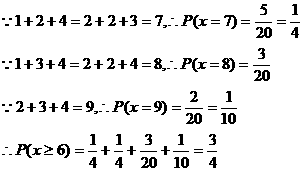
　 (II)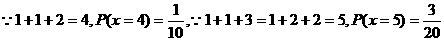

　　　　 ∴线路通过信息量的数学期望

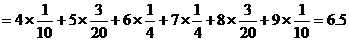
答：(I)线路信息畅通的概率是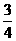.　 (II)线路通过信息量的数学期望是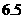

4．某学生语、数、英三科考试成绩，在一次考试中排名全班第一的概率：语文为，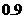

数学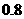为，英语为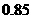，问一次考试中

　 　(Ⅰ)三科成绩均未获得第一名的概率是多少？

　 (Ⅱ)恰有一科成绩未获得第一名的概率是多少

解：分别记该生语、数、英考试成绩排名全班第一的事件为，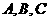

则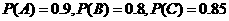　

　 (Ⅰ)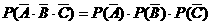

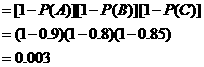
答：三科成绩均未获得第一名的概率是

　 (Ⅱ)()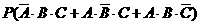

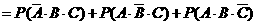
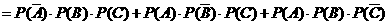
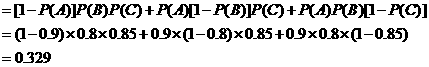
答：恰有一科成绩未获得第一名的概率是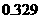

3． 奖器有个小球，其中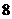个小球上标有数字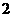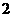，个小球上标有数字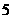，现摇出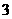个小球，规定所得奖金(元)为这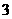个小球上记号之和，求此次摇奖获得奖金数额的数学期望

解：设此次摇奖的奖金数额为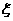元，

当摇出的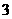个小球均标有数字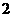时，；

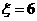当摇出的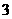个小球中有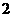个标有数字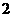，1个标有数字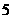时，；

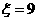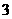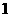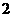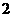当摇出的个小球有个标有数字，个标有数字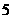时，。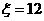

所以，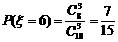　　 　　　

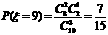
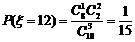
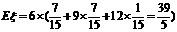
　 答：此次摇奖获得奖金数额的数字期望是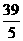元　

2． 出租车司机从饭店到火车站途中有六个交通岗，假设他在各交通岗到红灯这一事件是相互独立的，并且概率都是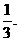

　 (1)求这位司机遇到红灯前，已经通过了两个交通岗的概率；

　 (2)求这位司机在途中遇到红灯数ξ的期望和方差。

解：(1)因为这位司机第一、二个交通岗未遇到红灯，在第三个交通岗遇到红灯，

所以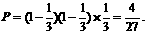　

(2)易知　 ∴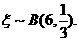　

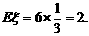
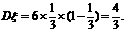
1． 人忘记了电话号码的最后一个数字，因而他随意地拨号，假设拨过了的号码不再重复，试求下列事件的概率：

　 (1)第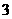次拨号才接通电话；　

(2)拨号不超过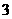次而接通电话.

解：设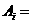{第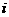次拨号接通电话}，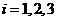

(1)第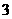次才接通电话可表示为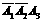于是所求概率为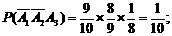

(2)拨号不超过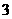次而接通电话可表示为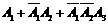：于是所求概率为

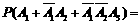
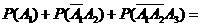
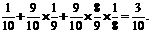
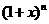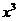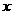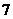6．(1)若的展开式中，的系数是的系数的倍，求；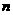

(2)已知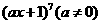的展开式中, 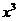的系数是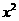的系数与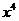的系数的等差中项,求;

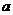(3)已知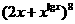的展开式中,二项式系数最大的项的值等于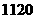,求.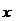

离散型随机变量解答题精选(选修2--3)

5．求证：.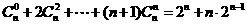

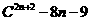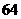4．用二次项定理证明能被整除.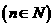

3．求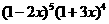展开式中按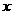的降幂排列的前两项.