
题目列表(包括答案和解析)
31.(2009江西卷理)已知向量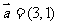 ,
,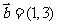 ,
,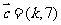 ,若
,若 ∥
∥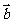 ,则
,则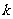 =
.
=
.
答案: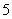
[解析]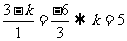
30.(2009江西卷文)已知向量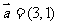 ,
,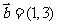 ,
,
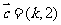 ,若
,若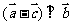 则
则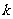 =
.
=
.
答案: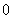
[解析]因为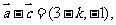 所以
所以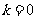 .
.
29.(2008海南卷13)已知向量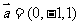 ,
,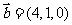 ,
,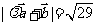 且
且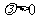 ,则
,则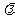 = _____3
= _____3
解析:由题意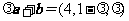
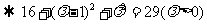
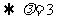

28.(2008浙江卷11)已知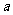 >0,若平面内三点A(1,-
>0,若平面内三点A(1,-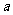 ),B(2,
),B(2,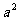 ),C(3,
),C(3,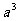 )共线,则
)共线,则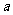 =________。
=________。
解析:本小题主要考查三点共线问题。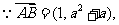
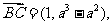
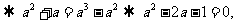
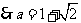 (舍负).
(舍负).
27.(2008江西卷13)直角坐标平面上三点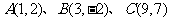 ,若
,若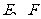 为线段
为线段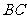 的三等分点,则
的三等分点,则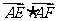 = .22
= .22

解析:由已知得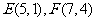 ,则
,则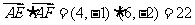
26. (2008天津卷14)已知平面向量
(2008天津卷14)已知平面向量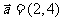 ,
,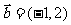 .若
.若 ,则
,则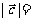 _____________.
_____________.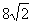
解析:令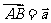 ,
,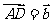 ,则
,则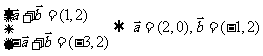
所以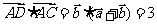 .
.
25.(2008北京卷10)已知向量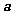 与
与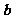 的夹角为
的夹角为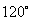 ,且
,且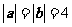 ,那么
,那么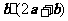 的值为 .
的值为 .
[标准答案]: 0
[试题分析]: 利用数形结合知,向量a与2a+b垂直。
[高考考点]: 向量运算的几何意义
[易错提醒]: 如果使用直接法,易出现计算错误。
[备考提示]: 向量的共线、平行、垂直、构成特殊三角形、特殊四边形等希望引起考生注意。
24.(2008全国二13)设向量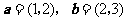 ,若向量
,若向量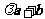 与向量
与向量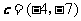 共线,则
共线,则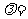 .
.
解析: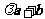 =
=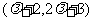 则向量
则向量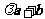 与向量
与向量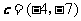 共线
共线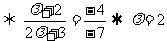
23.(2008陕西卷15)关于平面向量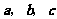 .有下列三个命题:
.有下列三个命题:
①若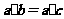 ,则
,则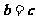 .②若
.②若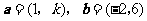 ,
,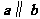 ,则
,则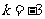 .
.
③非零向量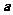 和
和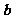 满足
满足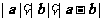 ,则
,则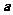 与
与 的夹角为
的夹角为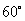 .
.
其中真命题的序号为 .(写出所有真命题的序号)
解析:①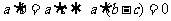 ,向量
,向量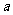 与
与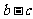 垂直
垂直
②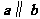
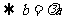
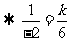
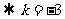
③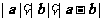
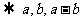 构成等边三角形,
构成等边三角形,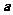 与
与 的夹角应为
的夹角应为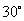

所以真命题只有②。
22.(2009湖北卷文)若向量a=(1,1),b=(-1,1),c=(4,2),则c=
A.3a+b B. 3a-b C.-a+3b D. a+3b
[答案]B
[解析]由计算可得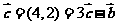 故选B
故选B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com