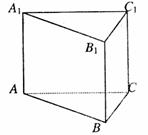
13. 已知正三棱柱ABC-A₁B₁C₁的底边长为1，高为h(h>3)，点M在侧棱BB₁上移动，到底面ABC的距离为x，且AM与侧面BCC₁所成的角为α；

　 　 (Ⅰ)(本问6分)若α在区间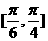上变化，求x的变化范围；

　 (Ⅱ)(本问6分)若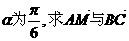所成的角.

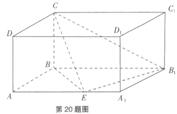
12. 已知长方体ABCD-A₁B₁C₁D₁中，E为AA₁上一点，平面B₁CE⊥平面BCE，AB=BC=1，AA₁=2。

(1)求平面B₁CE与平面B₁BE所成二面角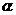的大小；(文科只要求求tan)

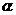(2)求点A到平面B₁CE的距离。

11. 如图，在正方体ABCD-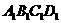中，E、F分别是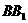，CD的中点．

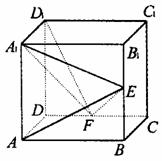　(1)证明：AD⊥；

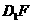　(2)求AE与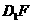所成的角；

　(3)证明：面AED⊥面；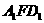

　(4)设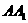＝2，求三棱锥F-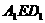的体积．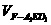

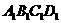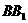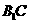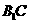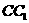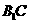10. 已知长方体ABCD-中，棱AB＝BC＝3，＝4，连结，过B点作的垂线交于E，交于F．

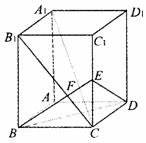
　(1)求证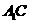：⊥平面EBD；

　(2)求ED与平面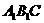所成角的大小；

　(3)求二面角E-BD-C的大小．

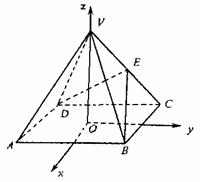
9. 如图，以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz，其中Ox∥BC，Oy∥AB，E为VC中点，正四棱锥底面边长为2a，高为h．

(1)求cos(，)；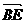

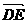(2)记面BCV为 ，面DCV为，若∠BED是二面角VC-的平面角，求∠BED．

8. 如图．已知斜三棱柱ABC-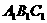的各棱长均为2，侧棱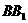与底面ABC所成角为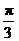，且侧面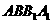垂直于底面ABC．

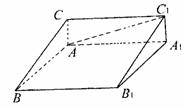(1)求证：点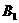在平面ABC上的射影为AB的中点；

(2)求二面角C-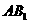-B的大小；

(3)判断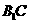与是否垂直，并证明你的结论．

7. 如图，已知正四棱柱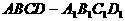的底面边长为3，侧棱长为4，连结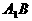，过A作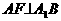，垂足为F，且AF的延长线交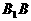于E。

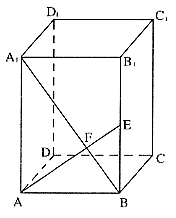
　　 (I)求证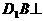：平面AEC

　　 (II)求三棱锥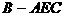的体积

　　 (III)求二面角的正切值。

6. 在直角梯形ABCD中，∠A=∠D=90°，AB＜CD，SD⊥平面ABCD，AB=AD=a，

S D=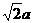，在线段SA上取一点E(不含端点)使EC=AC，截面CDE与SB交于点F。

(Ⅰ)求证：四边形EFCD为直角梯形；

(Ⅱ)求二面角B-EF-C的平面角的正切值；

(Ⅲ)设SB的中点为M，当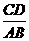的值是多少时，能使△DMC为直角三角形？请给出证明。

5. 已知直三棱柱ABC-A₁B₁C₁中，△ABC为等腰直角三角形，∠BAC＝90°，且AB＝AA₁，D、E、F分别为B₁A、C₁C、BC的中点。

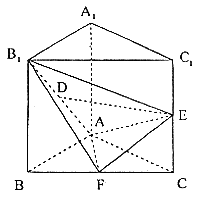
　　 (I)求证：DE∥平面ABC；

　　 (II)求证：B₁F⊥平面AEF；

　　 (III)求二面角B₁-AE-F的大小(用反三角函数表示)。

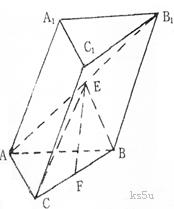
4. 如图，斜三棱柱ABC-A₁B₁C₁的底面是直角三角形，AC⊥CB，∠ABC=45°，侧面

A₁ABB₁是边长为a的菱形，且垂直于底面ABC，∠A₁AB=60°，E、F分别是AB₁、

BC的中点.

　 (1)求证EF//平面A₁ACC₁；

　 (2)求EF与侧面A₁ABB₁所成的角；

　 (3)求三棱锥A-BCE的体积.