
题目列表(包括答案和解析)
(1)平面向量的实际背景及基本概念
通过力和力的分析等实例,了解向量的实际背景,理解平面向量和向量相等的含义,理解向量的几何表示;
(2)向量的线性运算
①通过实例,掌握向量加、减法的运算,并理解其几何意义;
②通过实例,掌握向量数乘的运算,并理解其几何意义,以及两个向量共线的含义;
③了解向量的线性运算性质及其几何意义
(3)平面向量的基本定理及坐标表示
①了解平面向量的基本定理及其意义;
②掌握平面向量的正交分解及其坐标表示;
③会用坐标表示平面向量的加、减与数乘运算;
④ 理解用坐标表示的平面向量共线的条件
5.突出向量与其它数学知识的交汇
“新课程增加了新的现代数学内容,其意义不仅在于数学内容的更新,更重要的是引入新的思维方法,可以更有效地处理和解决数学问题和实际应用问题”。因此,新课程卷中有些问题属于新教材与旧教材的结合部,凡涉及此类问题,高考命题都采用了新旧结合,以新带旧或以新方法解决的方法进行处理,从中启示我们在高考学习中,应突出向量的工具性,注重向量与其它知识的交汇与融合,但不宜“深挖洞”。我们可以预测近两年向量高考题的难度不会也不应该上升到压轴题的水平
4.注重数学思想方法的教学
①.数形结合的思想方法。
由于向量本身具有代数形式和几何形式双重身份,所以在向量知识的整个学习过程中,都体现了数形结合的思想方法,在解决问题过程中要形成见数思形、以形助数的思维习惯,以加深理解知识要点,增强应用意识。
②.化归转化的思想方法。
向量的夹角、平行、垂直等关系的研究均可化归为对应向量或向量坐标的运算问题;三角形形状的判定可化归为相应向量的数量积问题;向量的数量积公式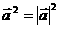 ,沟通了向量与实数间的转化关系;一些实际问题也可以运用向量知识去解决。
,沟通了向量与实数间的转化关系;一些实际问题也可以运用向量知识去解决。
③.分类讨论的思想方法。
如向量可分为共线向量与不共线向量;平行向量(共线向量)可分为同向向量和反向向量;向量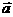 在
在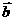 方向上的投影随着它们之间的夹角的不同,有正数、负数和零三种情形;定比分点公式中的
方向上的投影随着它们之间的夹角的不同,有正数、负数和零三种情形;定比分点公式中的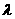 随分点P的位置不同,可以大于零,也可以小于零。
随分点P的位置不同,可以大于零,也可以小于零。
3.向量知识,向量观点在数学.物理等学科的很多分支有着广泛的应用,而它具有代数形式和几何形式的“双重身份”能融数形于一体,能与中学数学教学内容的许多主干知识综合,形成知识交汇点,所以高考中应引起足够的重视. 数量积的主要应用:①求模长;②求夹角;③判垂直;
2.平面向量数量积的运算律
特别注意:
(1)结合律不成立: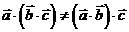 ;
;
(2)消去律不成立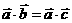 不能得到
不能得到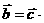 ;
;
(3)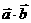 =0不能得到
=0不能得到 =
=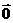 或
或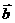 =
=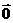 。
。
1.两个向量的数量积与向量同实数积有很大区别
(1)两个向量的数量积是一个实数,不是向量,符号由cosq的符号所决定;
(2)两个向量的数量积称为内积,写成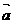 ·
·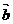 ;今后要学到两个向量的外积
;今后要学到两个向量的外积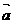 ×
×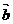 ,而
,而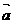 ×
× 是两个向量的数量的积,书写时要严格区分.符号“· ”在向量运算中不是乘号,既不能省略,也不能用“×”代替;
是两个向量的数量的积,书写时要严格区分.符号“· ”在向量运算中不是乘号,既不能省略,也不能用“×”代替;
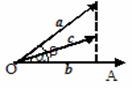 (3)在实数中,若a¹0,且a×b=0,则b=0;但是在数量积中,若
(3)在实数中,若a¹0,且a×b=0,则b=0;但是在数量积中,若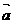 ¹0,且
¹0,且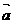 ×
×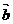 =0,不能推出
=0,不能推出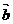 =
=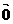 。因为其中cosq有可能为0;
。因为其中cosq有可能为0;
(4)已知实数a、b、c(b¹0),则ab=bc Þ a=c。但是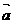 ×
×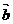 =
= 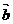 ×
×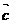
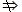
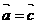 ;
;
如右图: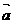 ×
×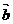 = |
= |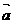 |
|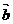 |cosb = |
|cosb = |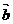 ||OA|,
||OA|,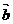 ×c = |
×c = |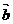 |c|cosa = |
|c|cosa = |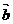 ||OA|Þ
||OA|Þ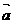 ×
×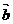 =
=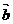 ×
×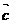 ,但
,但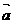 ¹
¹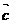 ;
;
(5)在实数中,有(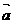 ×
×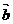 )
)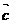 =
= 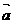 (
(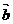 ×
×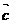 ),但是(
),但是(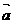 ×
×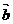 )
)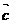 ¹
¹ 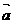 (
(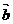 ×
×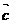 ),显然,这是因为左端是与c共线的向量,而右端是与
),显然,这是因为左端是与c共线的向量,而右端是与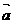 共线的向量,而一般
共线的向量,而一般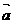 与c不共线。
与c不共线。
20. 在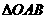 中,
中,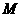 为
为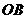 的中点,
的中点,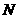 为
为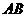 的中点,
的中点,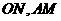 交于点
交于点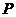 ,若
,若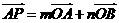 (
(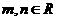 ),则
),则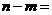 1
1
19. 已知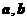 是两个互相垂直的单位向量, 且
是两个互相垂直的单位向量, 且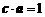 ,
,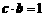 ,
,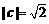 ,则对任意的正实数
,则对任意的正实数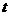 ,
,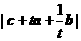 的最小值是
的最小值是 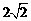 .
.
18. 若正方形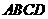 边长为1,点
边长为1,点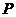 在线段
在线段 上运动,则
上运动,则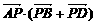 的取值范围是 .[-2,
的取值范围是 .[-2,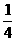 ]
]
17. 在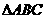 中,
中,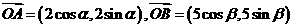 ,若
,若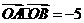 ,
,
则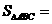
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com