
题目列表(包括答案和解析)
5.设函数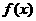 的导数为
的导数为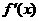 ,且
,且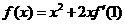 ,则
,则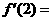
 已知曲线
已知曲线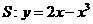
(1)求曲线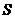 在点
在点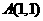 处的切线方程;(2)求过点
处的切线方程;(2)求过点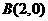 并与曲线
并与曲线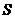 相切的直线方程.
相切的直线方程.
4.若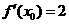 ,则
,则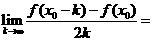
3.设点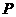 是曲线
是曲线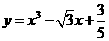 上的任意一点,点
上的任意一点,点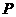 处切线的倾斜角为
处切线的倾斜角为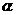 ,则角
,则角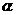 的取值范围是
( )
的取值范围是
( )

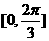

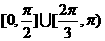

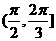

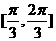
2.已知质点运动的方程为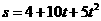 ,则该质点在
,则该质点在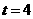 时的瞬时速度为( )
时的瞬时速度为( )

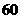
 120
120
 80
80  50
50
1.曲线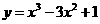 在点
在点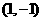 处的切线方程为 ( )
处的切线方程为 ( )

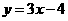

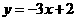

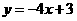

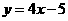
例1.(1)设函数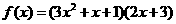 ,求
,求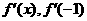 ;
;
(2)设函数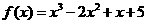 ,若
,若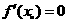 ,求
,求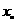 的值.
的值.
(3)设函数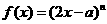 ,求
,求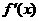 .
.
解:(1)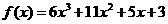 ,∴
,∴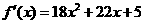
(2)∵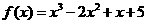 ,∴
,∴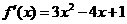
由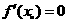 得:
得: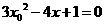 ,解得:
,解得: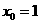 或
或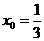
(3)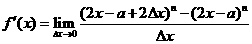
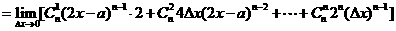
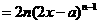
例2.物体在地球上作自由落体运动时,下落距离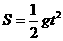 其中
其中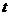 为经历的时间,
为经历的时间,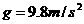 ,若
,若 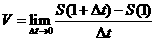
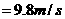 ,则下列说法正确的是(
,则下列说法正确的是(  )
)
(A)0-1s时间段内的速率为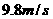
(B)在1-1+△ts时间段内的速率为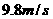
(C)在1s末的速率为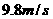
(D)若△t>0,则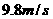 是1-1+△ts时段的速率;
是1-1+△ts时段的速率;
若△t<0,则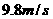 是1+△ts-1时段的速率.
是1+△ts-1时段的速率.
小结:本例旨在强化对导数意义的理解,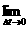
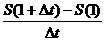 中的△t可正可负
中的△t可正可负
例3.(1)曲线 :
: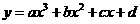 在
在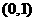 点处的切线为
点处的切线为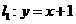 在
在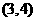 点处的切线为
点处的切线为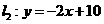 ,求曲线
,求曲线 的方程;
的方程;
(2)求曲线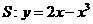 的过点
的过点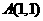 的切线方程.
的切线方程.
解:(1)已知两点均在曲线C上. ∴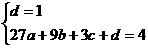
∵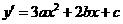
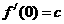
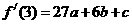
∴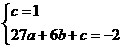 ,
可求出
,
可求出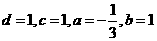
∴曲线 :
: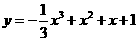
(2)设切点为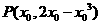 ,则斜率
,则斜率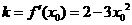 ,过切点的切线方程为:
,过切点的切线方程为: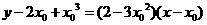 ,
,
∵过点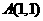 ,∴
,∴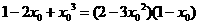
解得: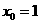 或
或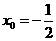 ,当
,当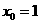 时,切点为
时,切点为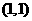 ,切线方程为:
,切线方程为: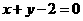
当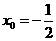 时,切点为
时,切点为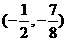 ,切线方程为:
,切线方程为: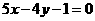
例4.设函数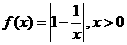 (1)证明:当
(1)证明:当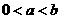 且
且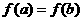 时,
时,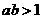 ;
;
(2)点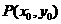 (0<x0<1)在曲线
(0<x0<1)在曲线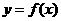 上,求曲线上在点
上,求曲线上在点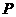 处的切线与
处的切线与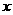 轴,
轴,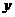 轴正向所围成的三角形面积的表达式.(用
轴正向所围成的三角形面积的表达式.(用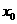 表示)
表示)
解:(1)∵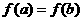 ,∴
,∴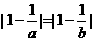 ,两边平方得:
,两边平方得:
即: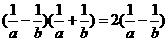 ,
,
∵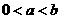 ,∴
,∴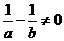 ,∴
,∴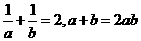
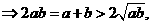 ∴
∴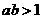
(2)当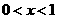 时,
时,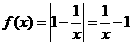 ,
,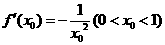
曲线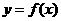 在点
在点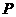 处的切线方程为:
处的切线方程为: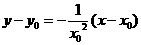 ,
,
即: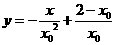
∴切线与与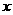 轴,
轴,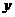 轴正向的交点为
轴正向的交点为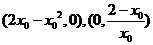
∴所求三角形的面积为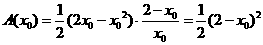
例5.求函数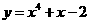 图象上的点到直线
图象上的点到直线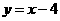 的距离的最小值及相应点的坐标.
的距离的最小值及相应点的坐标.
解:首先由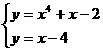 得
得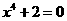 知,两曲线无交点.
知,两曲线无交点.
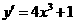 ,要与已知直线平行,须
,要与已知直线平行,须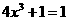 ,
,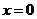
故切点:(0 , -2). 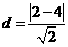
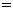
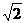 .
.
6.曲线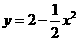 与
与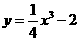 在交点处的切线的夹角是
在交点处的切线的夹角是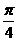 .
.
5.已知曲线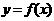 在
在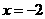 处的切线的倾斜角为
处的切线的倾斜角为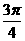 ,则
,则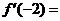
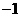 ,
,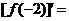
 .
.
4.若函数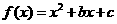 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数 的图象是(
的图象是(  )
)
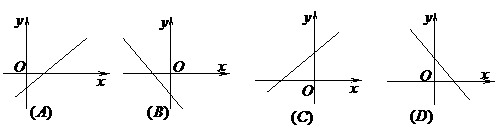
3.曲线 上两点
上两点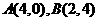 ,若曲线上一点
,若曲线上一点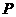 处的切线恰好平行于弦
处的切线恰好平行于弦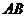 ,则点
,则点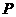 的坐标为
(
的坐标为
( 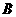 )
)




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com