
题目列表(包括答案和解析)
23.用总长44.8m的钢条制做一个底面是等腰三角形的直三棱柱容器的框架,如果所制做容器的底面的腰长比底边长的一半长1m,那么底面的底边,腰及容器的高为多少时容器的容积最大?(参考数据2.662=7.0756,3.342=11.1556)
解:设容器底面等腰三角形的底边长为2xm,则腰长为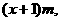 (1分)高为
(1分)高为
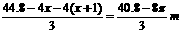 (2分)设容器的容积为Vm3,底面等腰三角形底边上的高
(2分)设容器的容积为Vm3,底面等腰三角形底边上的高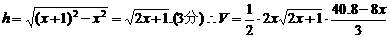
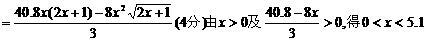
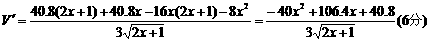
令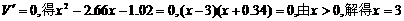
当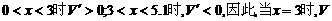 有最大值.
有最大值.
这时容器的底面等腰三角形的底边长为6m,腰长为4m,容器的高为5.6m。
|

|
版权所有:()
版权所有:()
22.已知椭圆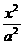 +
+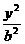 =1,(a>b>0)的长轴为AB,以AB为底边作椭圆的内接等腰梯形ABCD,求此等腰梯形面积的最大值。
=1,(a>b>0)的长轴为AB,以AB为底边作椭圆的内接等腰梯形ABCD,求此等腰梯形面积的最大值。
答案: 。
。
21.设函数f(x)=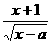 (a∈R),为使f(x)在区间(0,+∞)上为增函数,求a的取值范围。
(a∈R),为使f(x)在区间(0,+∞)上为增函数,求a的取值范围。
答案:a≤-1/2。
20.(本大题满分12分)
做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积价格为b元,问锅炉的直每径与高的比为多少时,造价最低?
答案:b/a。
19.设x=-2与x=4是函数f(x)=x3+ax2+bx的两个极值点。
(1)求常数a、b的值;
(2)判断函数在x=-2,x=4处的值是函数的极大值还是极小值,并说明理由。
答案:a=13 b=-24 f(-2)为极大值 f(4)极小值。
18.已知f(x)是R上的可导函数.
(1)f(-x)在x=a处的导数值与f(x)在x=-a处的导数值有什么关系?
(2)若f(x)为偶函数,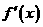 的奇偶性如何?
解:(1)互为相反数.
(2)f(-x)在x=-a处的导数值为:
的奇偶性如何?
解:(1)互为相反数.
(2)f(-x)在x=-a处的导数值为:
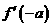 =
=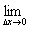
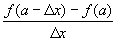 =-
=-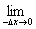
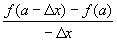 =-
=-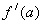
是奇函数,这是因为f(x)为偶函数,故可进而写为:
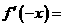
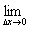
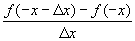 =-
=-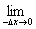
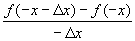 =-
=-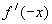 .
.
17. 已知函数f(x)=x2(x-1),若 =x0,求x0的值.
=x0,求x0的值.
解:f(x)=x3-x2,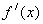 =3x2-2x, 令3x
=3x2-2x, 令3x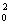 -2x0=x0知x0=0或1.
-2x0=x0知x0=0或1.
16.已知函数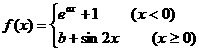 在R上可导,则a= ,b= .
在R上可导,则a= ,b= .
(a=2,b=2)
15.函数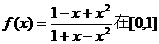 上的最小值是
. (
上的最小值是
. (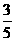 )
)
14.设函数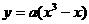 的递减区间为
的递减区间为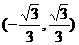 ,则a的取值范围是
,则a的取值范围是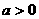
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com