
题目列表(包括答案和解析)
3.(2009韶关一模)已知函数 ,若实数
,若实数 是方程
是方程 的解,且
的解,且 ,则
,则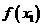 的值为
的值为
A.恒为正值 B.等于 C.恒为负值 D.不大于
C.恒为负值 D.不大于
答案 A
2.(2009枣庄一模)如果函数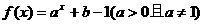 的图象经过第一、二、四象限,不经过第三象限,那么一定有 ( )
的图象经过第一、二、四象限,不经过第三象限,那么一定有 ( )
A. B.
B.
C. D.
D.
答案 B
1.(2009宣威六中第一次月考)已知函数 在区间
在区间 上是减函数,那么
上是减函数,那么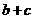 ( B )
( B )
A.有最大值 B.有最大值
B.有最大值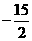 C.有最小值
C.有最小值 D.有最小值
D.有最小值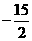
答案 B
6. (玉溪一中期中理)(本小题12分)已知函数 .
.
(Ⅰ) 设 .试证明
.试证明 在区间
在区间
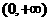 内是增函数;
内是增函数;
(Ⅱ) 若存在唯一实数 使得
使得 成立,求正整数
成立,求正整数 的值;
的值;
(Ⅲ) 若 时,
时, 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值.
证明:
(1) 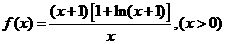

∴ 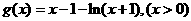 , 则
, 则 ∴
∴  在
在 内单调递增 解:(2) ∵
内单调递增 解:(2) ∵ ,
, ,∴由(1)可得
,∴由(1)可得 在
在 内单调递增, 即
内单调递增, 即 存在唯一根
存在唯一根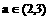 ∴
∴ 
解:(3) 由 得
得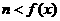 且
且  恒成立,由(2)知存在唯一实数
恒成立,由(2)知存在唯一实数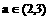 ,
,
使 且当
且当 时,
时, ,∴
,∴  ,当
,当 时,
时, ,∴
,∴ .
.
∴ 当 时,
时, 取得最小值
取得最小值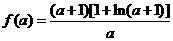
∵  ,
∴
,
∴  .
于是,
.
于是, ∵
∵ 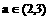 ,
,
∴ ∴
∴ ,故正整数
,故正整数 的最大值为3.
的最大值为3.
5. (三明市三校联考)(本小题满分14分)
已知函数 。
。
(I)求函数 的单调区间;
的单调区间;
(Ⅱ)若 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;
(Ⅲ)证明:① 上恒成立
上恒成立
②
解:(I)函数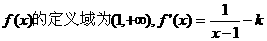
当 时
时 ,则
,则 上是增函数
上是增函数
当 时,若
时,若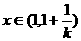 时有
时有
若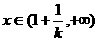 时有
时有 则
则 上是增函数,在
上是增函数,在 上是减函数
……………………(4分)
上是减函数
……………………(4分)
(Ⅱ)由(I)知 ,时
,时 递增,而
递增,而 不成立,故
不成立,故
又由(I)知 ,要使
,要使 恒成立,
恒成立,
则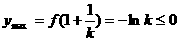 即可。 由
即可。 由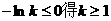 …………………(8分)
…………………(8分)
(Ⅲ)由(Ⅱ)知,当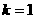 时有
时有 恒成立,且
恒成立,且 上是减函数,
上是减函数, ,
, 恒成立,
恒成立,
即 上恒成立
。……………………(11分)
上恒成立
。……………………(11分)
令 ,则
,则 ,即
,即 ,从而
,从而 ,
,
 成立……(14分)
成立……(14分)
4.(本小题满分13分)(安徽两地三校国庆联考)
定义在R上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)f(b),
求证:f(0)=1;
求证:对任意的x∈R,恒有f(x)>0;
(3)证明:f(x)是R上的增函数;
(4)若f(x)·f(2x-x2)>1,求x的取值范围。
解 (1)令a=b=0,则f(0)=[f(0)]2∵f(0)≠0 ∴f(0)=1
(2)令a=x,b=-x则 f(0)=f(x)f(-x)
∴
由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0
∴ 又x=0时,f(0)=1>0
又x=0时,f(0)=1>0
∴对任意x∈R,f(x)>0
(3)任取x2>x1,则f(x2)>0,f(x1)>0,x2-x1>0
∴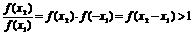
∴f(x2)>f(x1) ∴f(x)在R上是增函数
(4)f(x)·f(2x-x2)=f[x+(2x-x2)]=f(-x2+3x)又1=f(0),
f(x)在R上递增
∴由f(3x-x2)>f(0)得:3x-x2>0 ∴ 0<x<3
3.(本小题满分12分)(安徽两地三校国庆联考)
已知a是实数,函数 ,如果函数
,如果函数 在区间
在区间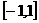 上有零点,求a的取值范围.
上有零点,求a的取值范围.
解:若 ,
, 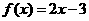 ,显然在
,显然在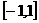 上没有零点, 所以
上没有零点, 所以  .
.
令  , 解得
, 解得 
①当  时,
时, 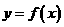 恰有一个零点在
恰有一个零点在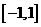 上;
上;
②当 ,即
,即 时,
时,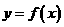 在
在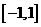 上也恰有一个零点.
上也恰有一个零点.
③当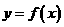 在
在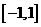 上有两个零点时, 则
上有两个零点时, 则
 或
或
解得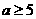 或
或
综上所求实数 的取值范围是
的取值范围是  或
或  .
.
2.(本小题满分12分)(安徽两地三校国庆联考)
机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值);
(3)使用若干年后,对机床的处理方案有两种:
(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
解 (1)依题得: (x
(x N*)
N*)
(2)解不等式
∵x N*,∴3≤x≤17,故从第3年开始盈利。
N*,∴3≤x≤17,故从第3年开始盈利。
(3)(Ⅰ)
当且仅当 时,即x=7时等号成立.
时,即x=7时等号成立.
 到2008年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.
到2008年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.
(Ⅱ)y=-2x2+40x-98=-(x-10)2+102,当x=10时,ymax=102
故到2011年,盈利额达到最大值,工厂获利102+12=114万元
盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理.
1.(本题满分14分)已知函数
⑴求函数 的周期;
的周期;
⑵函数 的图象可由函数
的图象可由函数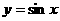 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
解:(1)

所以 函数 的周期是
的周期是
(2)将函数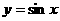 的图象向左平移
的图象向左平移 个单位,再将所得图象上每一点的横坐标变为原来的
个单位,再将所得图象上每一点的横坐标变为原来的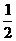 倍(纵坐标不变式),得函数
倍(纵坐标不变式),得函数 的图象
的图象
8.(昆明一中二次月考理)直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f(x)的图象恰好通过k(k∈N*)个格点,则称函数f(x)为k阶格点函数。下列函数:
①f(x)=sinx; ②f(x)=π(x-1)2+3; ③ ④
④ ,
,
其中是一阶格点函数的有 .
答案:①②④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com