
题目列表(包括答案和解析)
2.(2009昆明市期末)在△ABC中,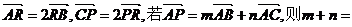
( )
A.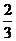 B
B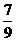
C.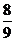 D.1
D.1
答案 B
3、(2009临沂一模)已知向量m=(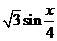 ,1),n=(
,1),n=(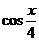 ,
,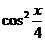 )。
)。
(1)若m•n=1,求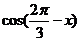 的值;
的值;
(2)记f(x)=m•n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足
(2a-c)cosB=bcosC,求函数f(A)的取值范围。
解:(I)m•n=
=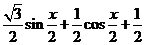
=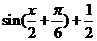
∵m•n=1
∴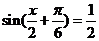 ┉┉┉┉┉┉┉┉┉┉┉┉┉4分
┉┉┉┉┉┉┉┉┉┉┉┉┉4分
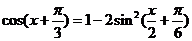
=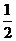
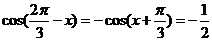 ┉┉┉┉┉┉┉6分
┉┉┉┉┉┉┉6分
(II)∵(2a-c)cosB=bcosC
由正弦定理得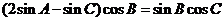 ┉┉┉┉┉┉7分
┉┉┉┉┉┉7分
∴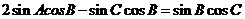
∴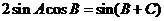
∵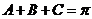
∴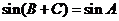 ,且
,且
∴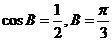 ┉┉┉┉┉┉8分
┉┉┉┉┉┉8分
∴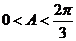 ┉┉┉┉┉┉9分
┉┉┉┉┉┉9分
∴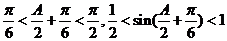 ┉┉┉┉┉┉10分
┉┉┉┉┉┉10分
又∵f(x)=m•n=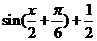 ,
,
∴f(A)=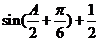 ┉┉┉┉┉┉11分
┉┉┉┉┉┉11分
故函数f(A)的取值范围是(1,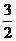 )┉┉┉┉┉┉12分
)┉┉┉┉┉┉12分
2009年联考题
2、(2009南华一中12月月考)已知A、B、C的坐标分别为A(4,0),B(0,4),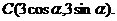
(1)若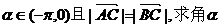 的值;
的值;
(2)若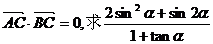 的值.
的值.
解:
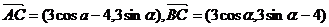 ,
,
(1)由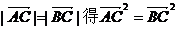 ,……………………… 2分
,……………………… 2分
即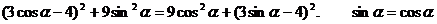
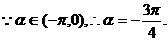 ……………………… 5分
……………………… 5分
(2)由 ,得
,得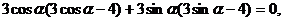
解得 两边平方得
两边平方得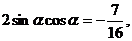 ……… 7分
……… 7分
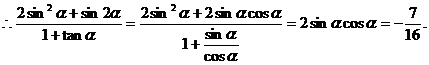 ………… 10分
………… 10分
1、(2009滨州一模)已知向量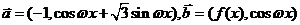 ,
,
其中 >0,且
>0,且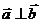 ,又
,又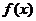 的图像两相邻对称轴间距为
的图像两相邻对称轴间距为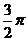 .
.
(Ⅰ)求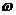 的值;
的值;
(Ⅱ) 求函数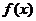 在[-
在[-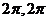 ]上的单调减区间.
]上的单调减区间.
(Ⅰ) 由题意

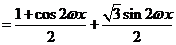

由题意,函数周期为3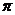 ,又
,又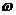 >0,
>0,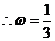 ;
;
(Ⅱ) 由(Ⅰ)知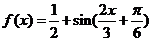
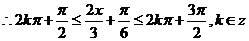
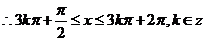
又x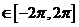 ,
,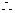
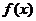 的减区间是
的减区间是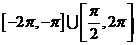 .
.
5、(2009闵行三中模拟)已知 ,
,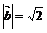 ,
,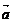 与
与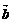 的夹角为
的夹角为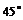 ,要使
,要使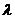
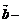
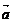 与
与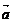 垂直,则
垂直,则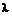 =
。
=
。
答案 2
4、(2009上海九校联考)若向量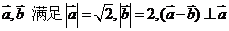 ,则向量
,则向量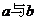 的夹角等于
的夹角等于
答案 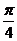
3、(2009上海卢湾区4月模考)在平面直角坐标系中,若 为坐标原点,则
为坐标原点,则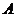 、
、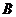 、
、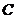 三点在同一直线上的充要条件为存在惟一的实数
三点在同一直线上的充要条件为存在惟一的实数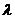 ,使得
,使得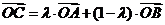 成立,此时称实数
成立,此时称实数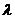 为“向量
为“向量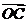 关于
关于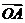 和
和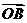 的终点共线分解系数”.若已知
的终点共线分解系数”.若已知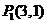 、
、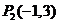 ,且向量
,且向量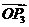 是直线
是直线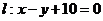 的法向量,则“向量
的法向量,则“向量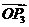 关于
关于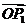 和
和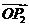 的终点共线分解系数”为
.
的终点共线分解系数”为
.
答案 -1
2、(2009上海十校联考)已知平面上直线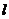 的方向向量
的方向向量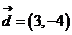 ,点
,点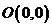 和
和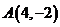 在
在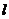 上的射影分别是
上的射影分别是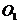 和
和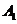 ,则
,则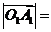 ________________
________________
答案4
1、(2009上海普陀区)设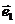 、
、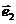 是平面内一组基向量,且
是平面内一组基向量,且 、
、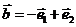 ,则向量
,则向量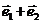 可以表示为另一组基向量
可以表示为另一组基向量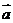 、
、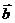 的线性组合,即
的线性组合,即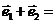
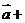
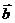 .
.
答案 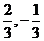 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com