
题目列表(包括答案和解析)
2.(2010湖南文)7.在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,c= a,则
a,则
A.a>b B.a<b
C. a=b D.a与b的大小关系不能确定

[命题意图]本题考查余弦定理,特殊角的三角函数值,不等式的性质,比较法,属中档题。
1.(2010上海文)18.若△ 的三个内角满足
的三个内角满足 ,则△
,则△
(A)一定是锐角三角形. (B)一定是直角三角形.
(C)一定是钝角三角形. (D)可能是锐角三角形,也可能是钝角三角形.
[答案]C
解析:由 及正弦定理得a:b:c=5:11:13
及正弦定理得a:b:c=5:11:13
由余弦定理得 ,所以角C为钝角
,所以角C为钝角
2010年高考题
10.(广东地区2008年01月份期末试题) 如图,直四棱柱
ABCD-A1B1C1D1的高为3,底面是边长为4
且∠DAB=60°的菱形,AC∩BD=O,A1C1∩B1D1=O1,
E是O1A的中点.
(1)求二面角O1-BC-D的大小;
(2)求点E到平面O1BC的距离.
解 (1)∵OO1⊥平面AC,
∴OO1⊥OA,OO1⊥OB,又OA⊥OB,
建立如图所示的空间直角坐标系(如图)
∵底面ABCD是边长为4,∠DAB=60°的菱形,
∴OA=2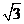 ,OB=2,
,OB=2,
则A(2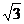 ,0,0),B(0,2,0),C(-2
,0,0),B(0,2,0),C(-2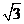 ,0,0),
,0,0),
O1(0,0,3)
设平面O1BC的法向量为 =(x,y,z),
=(x,y,z),
则 ⊥
⊥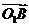 ,
, ⊥
⊥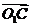 ,
,
∴ ,则z=2,则x=-
,则z=2,则x=-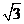 ,y=3,
,y=3,
∴ =(-
=(-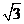 ,3,2),而平面AC的法向量
,3,2),而平面AC的法向量 =(0,0,3)
=(0,0,3)
∴cos< ,
, >=
>= ,
,
设O1-BC-D的平面角为α, ∴cosα=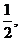 ∴α=60°.
∴α=60°.
故二面角O1-BC-D为60°.
(2)设点E到平面O1BC的距离为d,
∵E是O1A的中点,∴ =(-
=(-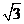 ,0,
,0, ),
),
则d= ,∴点E到面O1BC的距离等于
,∴点E到面O1BC的距离等于 .
.
9. (北京市西城区2008年4月高三抽样测试)如图,在三棱锥 中,
中,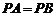 ,
,
 ,平面
,平面 平面
平面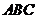 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求异面直线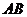 和
和 所成角的大小.
所成角的大小.
 作
作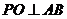 于点
于点 ,
,
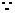 平面
平面 平面
平面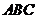 ,
,
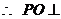 平面
平面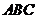 .
.
过点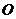 作
作 的平行线,交
的平行线,交 于点
于点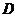 .
.
如图,以 为原点,直线
为原点,直线 分别为
分别为 轴,
轴,
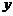 轴,
轴, 轴,建立空间直角坐标系 .
轴,建立空间直角坐标系 .
 .
. 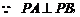
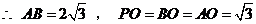 .
.
 ,
,
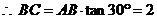 .
.



(Ⅰ)证明 

 .
.
又

 .
.
(Ⅱ)解 作 于点
于点 ,连结
,连结 .
.
 平面
平面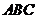 , 根据三垂线定理得
, 根据三垂线定理得  ,
,
 是二面角
是二面角 的平面角.
的平面角.
在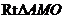 中,
中,  ,
,
 从而
从而 ,
,
 ,
,
即二面角 的大小是
的大小是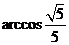 .
.

 (Ⅲ)解
(Ⅲ)解 ,
,
 ,
,
 异面直线
异面直线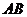 和
和 所成角的大小为arccos
所成角的大小为arccos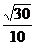 .
.
8. (北京市十一学校2008届高三数学练习题)如图,
在正四棱锥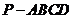 中,
中, ,点
,点 在
在
棱 上.
上.
(Ⅰ)问点 在何处时,
在何处时, ,并加以证明;
,并加以证明;
(Ⅱ)当 时,求点
时,求点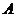 到平面
到平面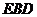 的距离;
的距离;
(Ⅲ)求二面角 的大小.
的大小.
解 (Ⅰ)当E为PC中点时, .
.
连接AC,且 ,由于四边形ABCD为正方形,
,由于四边形ABCD为正方形,
∴O为AC的中点,又E为中点,
∴OE为△ACP的中位线,
∴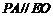 ,又
,又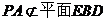 ,
,
∴ .
.
(Ⅱ)作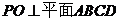 ,依题意
,依题意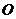 是正方形
是正方形 的中心,如图建立空间坐标系.
的中心,如图建立空间坐标系.
则 ,
, ,
, 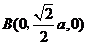 ,
, ,
, .
.
 ∴
∴ ,
, ,
,
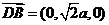 ,
, ,
,
设面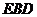 的法向量为
的法向量为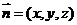

 ,
,
点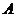 到平面
到平面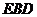 的距离为
的距离为 .
.
(Ⅲ)设二面角 的平面角为
的平面角为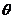 ,平面
,平面 的法向量为
的法向量为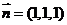 . 设平面
. 设平面 的法向量为
的法向量为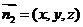 ,
,  .
.

 .
. 
7. (北京市东城区2008年高三综合练习二)如图,在四棱锥P-ABCD中,
(北京市东城区2008年高三综合练习二)如图,在四棱锥P-ABCD中,
平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,
△PAB等边三角形.
(1)求二面角B-AC-P的大小;
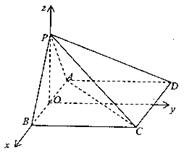 (2)求点A到平面PCD的距离.
(2)求点A到平面PCD的距离.
解 (1)建立如图的空间直角坐标系O-xyz,
则A(-1,0,0),B(1,0,0),
则P(0,0,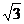 ),C(1,2,0)
),C(1,2,0)
设 为平面PAC的一个法向量,
为平面PAC的一个法向量,
则
又
 令z=1,得
令z=1,得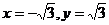
得
又 是平面ABC的一个法向量,
是平面ABC的一个法向量,
设二面角B-AC-P的大小为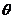 ,
,
则

(2)设 为平面PCD的一个法向量.
为平面PCD的一个法向量.
则 由D(-1,2,0),可知
由D(-1,2,0),可知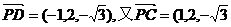 ),
), 可得a=0,令
可得a=0,令 ,则c=2.
,则c=2.
得 ,
,
设点A到平面PCD的距离为d,则
 ∴点A到平面PCD的距离为
∴点A到平面PCD的距离为
6. (安徽省巢湖市2008届高三第二次教学质量检测)如图,
 、
、 分别是正四棱柱
分别是正四棱柱 上、下底面的中
上、下底面的中
心, 是
是 的中点,
的中点, .
.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)当 时,求直线
时,求直线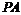 与平面
与平面 所成角的大小;
所成角的大小;
 (Ⅲ) 当
(Ⅲ) 当 取何值时,
取何值时, 在平面
在平面 内的射影恰好为
内的射影恰好为 的重心?
的重心?
以点 为原点,直线
为原点,直线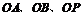 所在直线分别为
所在直线分别为 轴,
轴,
建立如图所示的空间直角坐标系,不妨设 ,
,
则得 、
、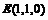 、
、 、
、 、
、
(Ⅰ)证明 由上得 、
、 、
、
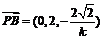 ,设
,设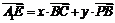 得
得

解得 , ∴
, ∴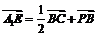
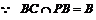 ,
, ∴
∴ ∥平面
∥平面
|
 时,由
时,由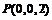 、
、 得
得 、
、 、
、
设平面 的法向量为
的法向量为 ,则由
,则由 ,得
,得 ,
,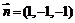
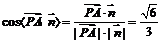 ,∴直线
,∴直线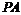 与平面
与平面 所成角的大小为
所成角的大小为 .
.
(Ⅲ) 解 由(Ⅰ)知 的重心
的重心 为
为 ,则
,则 ,
,
若 在平面
在平面 内的射影恰好为
内的射影恰好为 的重心,则有
的重心,则有 ,解得
,解得
∴当 时,
时, 在平面
在平面 内的射影恰好为
内的射影恰好为 的重心.
的重心.
5. (安徽省淮南市2008届高三第一次模拟考试)如图,正三棱柱ABC-
(安徽省淮南市2008届高三第一次模拟考试)如图,正三棱柱ABC- 的底面边长是2,D是侧棱C
的底面边长是2,D是侧棱C 的中点,直线AD与侧面
的中点,直线AD与侧面 所成的角为45°.
所成的角为45°.
( 1 )求二面角A-BD-C的大小;
(2)求点C到平面ABD的距离.
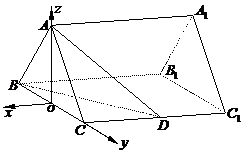 解 (1)如图,建立空间直角坐标系
解 (1)如图,建立空间直角坐标系 .
.
则 .
.
设
 为平面
为平面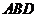 的法向量.
的法向量.
由 得
得
 .
.
 取
取
又平面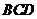 的一个法向量
的一个法向量

 .
.
结合图形可知,二面角 的大小为
的大小为 .
.
(Ⅲ)由(Ⅱ)知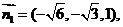


 点
点 到平面
到平面 的距离
的距离
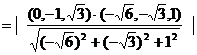 =
= .
.
4. ( 四川省成都市2008一诊) 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°.
(1) 求异面直线AF与BG所成的角的大小;
(2) 求平面APB与平面CPD所成的锐二面角的大小.
 解 由题意可知:AP、AD、AB两两垂直,可建立空间直角坐标系A-xyz
由平面几何知识知:AD=4, D (0,
4, 0), B (2 , 0 , 0 ),
C ( 2, 2, 0 ), P (0, 0, 2), E (0,
0, 1), F (1 ,0, 1), G (1 ,1 ,1)
(1)=(1,0,1),=(-1,1,1)
∴·=0,
∴AF与BG所成角为 .
(2) 可证明AD⊥平面APB,
∴平面APB的法向量为n=(0,1,0)
设平面CPD的法向量为m=(1,y,z)
由
解 由题意可知:AP、AD、AB两两垂直,可建立空间直角坐标系A-xyz
由平面几何知识知:AD=4, D (0,
4, 0), B (2 , 0 , 0 ),
C ( 2, 2, 0 ), P (0, 0, 2), E (0,
0, 1), F (1 ,0, 1), G (1 ,1 ,1)
(1)=(1,0,1),=(-1,1,1)
∴·=0,
∴AF与BG所成角为 .
(2) 可证明AD⊥平面APB,
∴平面APB的法向量为n=(0,1,0)
设平面CPD的法向量为m=(1,y,z)
由 Þ
故m=(1,1,2)
∵cos<m,n>=
∴平面APB与平面CPD所成的锐二面角的大小为arccos.
Þ
故m=(1,1,2)
∵cos<m,n>=
∴平面APB与平面CPD所成的锐二面角的大小为arccos.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com