
题目列表(包括答案和解析)
8.(2010江苏卷)17、(本小题满分14分)
某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE= ,∠ADE=
,∠ADE= 。
。
(1)该小组已经测得一组 、
、 的值,tan
的值,tan =1.24,tan
=1.24,tan =1.20,请据此算出H的值;
=1.20,请据此算出H的值;
(2) 该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使
该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使 与
与 之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,
之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时, -
- 最大?
最大?
[解析] 本题主要考查解三角形的知识、两角差的正切及不等式的应用。
(1) ,同理:
,同理: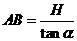 ,
, 。
。
AD-AB=DB,故得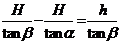 ,解得:
,解得: 。
。
因此,算出的电视塔的高度H是124m。
(2)由题设知 ,得
,得 ,
,

 ,(当且仅当
,(当且仅当 时,取等号)
时,取等号)
故当 时,
时, 最大。
最大。
因为 ,则
,则 ,所以当
,所以当 时,
时, -
- 最大。
最大。
故所求的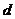 是
是 m。
m。
16、(2010安徽理数)(本小题满分12分)
设 是锐角三角形,
是锐角三角形, 分别是内角
分别是内角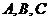 所对边长,并且
所对边长,并且
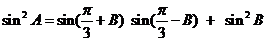 。
。
(Ⅰ)求角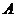 的值;
的值;
(Ⅱ)若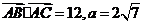 ,求
,求 (其中
(其中 )。
)。

7.(2010福建理)19.(本小题满分13分)
 。
。 ,轮船位于港口O北偏西
,轮船位于港口O北偏西 且与该港口相距20海里的A处,并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以
且与该港口相距20海里的A处,并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以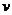 海里/小时的航行速度匀速行驶,经过t小时与轮船相遇。
海里/小时的航行速度匀速行驶,经过t小时与轮船相遇。
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。
[解析]如图,由(1)得
 而小艇的最高航行速度只能达到30海里/小时,故轮船与小艇不可能在A、C(包含C)的任意位置相遇,设
而小艇的最高航行速度只能达到30海里/小时,故轮船与小艇不可能在A、C(包含C)的任意位置相遇,设 ,OD=
,OD= ,
,
由于从出发到相遇,轮船与小艇所需要的时间分别为 和
和 ,
,
所以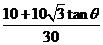
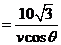 ,解得
,解得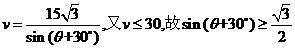 ,
,
从而 值,且最小值为
值,且最小值为 ,于是
,于是
当
 取得最小值,且最小值为
取得最小值,且最小值为 。
。
此时,在 中,
中, ,故可设计航行方案如下:
,故可设计航行方案如下:
航行方向为北偏东 ,航行速度为30海里/小时,小艇能以最短时间与轮船相遇。
,航行速度为30海里/小时,小艇能以最短时间与轮船相遇。
6.(2010全国卷1理)(17)(本小题满分10分)
已知 的内角
的内角 ,
, 及其对边
及其对边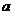
 ,
,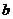
 满足
满足 ,求内角
,求内角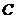 .
.

5.(2010天津理)(17)(本小题满分12分)
已知函数
(Ⅰ)求函数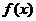 的最小正周期及在区间
的最小正周期及在区间 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若 ,求
,求 的值。
的值。
[解析]本小题主要考查二倍角的正弦与余弦、两角和的正弦、函数 的性质、同角三角函数的基本关系、两角差的余弦等基础知识,考查基本运算能力,满分12分。
的性质、同角三角函数的基本关系、两角差的余弦等基础知识,考查基本运算能力,满分12分。
(1)解:由 ,得
,得
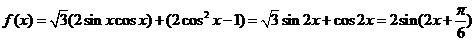
所以函数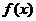 的最小正周期为
的最小正周期为
因为 在区间
在区间 上为增函数,在区间
上为增函数,在区间 上为减函数,又
上为减函数,又
 ,所以函数
,所以函数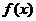 在区间
在区间 上的最大值为2,最小值为-1
上的最大值为2,最小值为-1
(Ⅱ)解:由(1)可知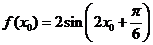
又因为 ,所以
,所以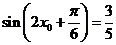
由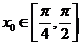 ,得
,得
从而
所以

4.(2010安徽文)16、(本小题满分12分)
 的面积是30,内角
的面积是30,内角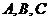 所对边长分别为
所对边长分别为 ,
,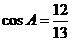 。
。
(Ⅰ)求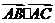 ;
;
(Ⅱ)若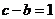 ,求
,求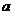 的值。
的值。
[命题意图]本题考查同角三角函数的基本关系,三角形面积公式,向量的数量积,利用余弦定理解三角形以及运算求解能力.
[解题指导](1)根据同角三角函数关系,由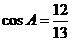 得
得 的值,再根据
的值,再根据 面积公式得
面积公式得 ;直接求数量积
;直接求数量积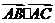 .由余弦定理
.由余弦定理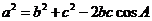 ,代入已知条件
,代入已知条件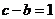 ,及
,及 求a的值.
求a的值.
解:由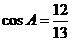 ,得
,得 .
.
又 ,∴
,∴ .
.
(Ⅰ) .
.
(Ⅱ)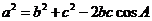
 ,
,
∴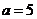 .
.
[规律总结]根据本题所给的条件及所要求的结论可知,需求 的值,考虑已知
的值,考虑已知 的面积是30,
的面积是30,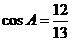 ,所以先求
,所以先求 的值,然后根据三角形面积公式得
的值,然后根据三角形面积公式得 的值.第二问中求a的值,根据第一问中的结论可知,直接利用余弦定理即可.
的值.第二问中求a的值,根据第一问中的结论可知,直接利用余弦定理即可.
(2010重庆文数)(18).(本小题满分13分), (Ⅰ)小问5分,(Ⅱ)小问8分.)
设 的内角A、B、C的对边长分别为a、b、c,且3
的内角A、B、C的对边长分别为a、b、c,且3 +3
+3 -3
-3 =4
=4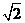 bc
.
bc
.
(Ⅰ) 求sinA的值;
(Ⅱ)求 的值.
的值.

3.(2010辽宁理)(17)(本小题满分12分)
在△ABC中,a, b, c分别为内角A, B, C的对边,且
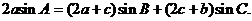
(Ⅰ)求A的大小;
(Ⅱ)求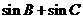 的最大值.
的最大值.
解:
(Ⅰ)由已知,根据正弦定理得
即 
由余弦定理得 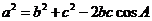
故 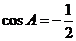 ,A=120°
……6分
,A=120°
……6分
(Ⅱ)由(Ⅰ)得:
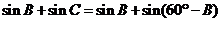

故当B=30°时,sinB+sinC取得最大值1。 ……12分
2.(2010辽宁文)(17)(本小题满分12分)
在 中,
中, 分别为内角
分别为内角 的对边,
的对边,
且
(Ⅰ)求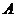 的大小;
的大小;
(Ⅱ)若 ,试判断
,试判断 的形状.
的形状.
解:(Ⅰ)由已知,根据正弦定理得
即
由余弦定理得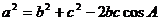
故
(Ⅱ)由(Ⅰ)得
又 ,得
,得
因为 ,
,
故
所以 是等腰的钝角三角形。
是等腰的钝角三角形。
1. (2010陕西文)17.(本小题满分12分)
(2010陕西文)17.(本小题满分12分)
在△ABC中,已知B=45°,D是BC边上的一点,
AD=10,AC=14,DC=6,求AB的长.
解 在△ADC中,AD=10,AC=14,DC=6,
由余弦定理得
cos
 =
=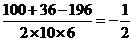 ,
,

 ADC=120°,
ADC=120°,  ADB=60°
ADB=60°
在△ABD中,AD=10,  B=45°,
B=45°,  ADB=60°,
ADB=60°,
由正弦定理得 ,
,
 AB=
AB= .
.
6.(2010江苏卷)13、在锐角三角形ABC,A、B、C的对边分别为a、b、c, ,则
,则 =_________。
=_________。
[解析] 考查三角形中的正、余弦定理三角函数知识的应用,等价转化思想。一题多解。
(方法一)考虑已知条件和所求结论对于角A、B和边a、b具有轮换性。
当A=B或a=b时满足题意,此时有: ,
,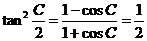 ,
, ,
,
 ,
, =
4。
=
4。
(方法二)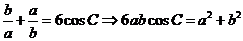 ,
,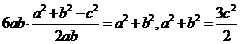

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com