
题目列表(包括答案和解析)
6、(2009昆明市期末)如图,在正三棱柱ABC-A1B1C1中,BB1=2,BC=2 ,D为B1C1的中点。
,D为B1C1的中点。
 (Ⅰ)证明:B1C⊥面A1BD;
(Ⅰ)证明:B1C⊥面A1BD;
(Ⅱ)求二面角B-AC-B1的大小。
方法一:
(Ⅰ)证明:在Rt△BB1D和Rt△B1C1C中,
由
 得
得
△BB1D∽△B1C1C,∠B1DB=∠B1CC1。
又 ∠CB1D+∠B1CC1=90°
故 ∠CB1D+∠B1DB=90°
故 B1C⊥BD.·····················3分
又 正三棱柱ABC-A1B1C1,D为B1C1的中点。
由 A1D⊥平面B1C,
得 A1D⊥B1C
又A1D∩B1D=D,
所以 B1C⊥面A1BD。···················································6分
(Ⅱ)解:设E为AC的中点,连接BE、B1E。
在正三棱柱ABC-A1B1C1中,B1C=B1A,∴B1E⊥AC,BE⊥AC,
即 ∠BEB1为二面角B-AC-B1的平面角·································9分
又

故

所以 二面角的大小为 ······································12分
······································12分
方法二:
(Ⅰ)证明:设BC的中点为O,如图建立空间直角坐标系O-xyz
依题意有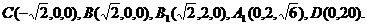
则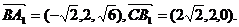
由
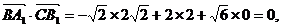
故 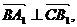
又 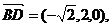
所以

故
 又 BD∩BA1=B
又 BD∩BA1=B
所以 B1C⊥面A1BD,
(Ⅱ)依题意有

设 ⊥平面ACB1,
⊥平面ACB1, ⊥平面ABC。
⊥平面ABC。
求得

故

所以 二面角的大小为 ······································12分
······································12分
5、(2009深圳一模)如图,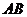 为圆
为圆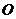 的直径,点
的直径,点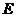 、
、 在圆
在圆 上,
上, ,矩形
,矩形 和圆
和圆 所在的平面互相垂直.已知
所在的平面互相垂直.已知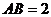 ,
, .
.
(Ⅰ)求证:平面 平面
平面 ;
;
 (Ⅱ)求直线
(Ⅱ)求直线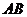 与平面
与平面 所成角的大小;
所成角的大小;
(Ⅲ)当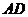 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为 ?
?
解:(Ⅰ)证明: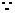 平面
平面 平面
平面 ,
, ,
,
平面 平面
平面 =
=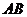 ,
,
 平面
平面 .
.
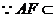 平面
平面 ,
, ,
,
又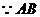 为圆
为圆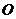 的直径,
的直径, ,
,
 平面
平面 .
.
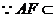 平面
平面 ,
, 平面
平面 平面
平面 . …………………4分
. …………………4分
(Ⅱ)根据(Ⅰ)的证明,有 平面
平面 ,
,
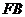 为
为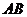 在
在
平面 上的射影,
上的射影,
因此, 为直线
为直线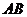 与平面
与平面 所成的角.
………………………5分
所成的角.
………………………5分
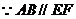 ,
, 四边形
四边形 为等腰梯形,
为等腰梯形,
过点 作
作 ,交
,交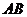 于
于 .
.
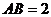 ,
, ,则
,则 .
.
在 中,根据射影定理
中,根据射影定理 ,得
,得 .…………………7分
.…………………7分
 ,
, .
.
 直线
直线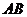 与平面
与平面 所成角的大小为
所成角的大小为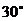 .
…………………8分
.
…………………8分
(Ⅲ)(解法一)过点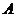 作
作 ,交
,交 的延长线于点
的延长线于点 ,连
,连 .
.
根据(Ⅰ)的证明, 平面
平面 ,则
,则 ,
,
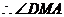 为二面角
为二面角 的平面角,
的平面角,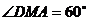 .…………………9分
.…………………9分
在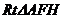 中,
中, ,
, ,
,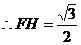 . ………………… 10分
. ………………… 10分
又 四边形
四边形 为矩形,
为矩形,
 .
.
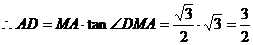 .
.
因此,当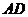 的长为
的长为 时,二面角
时,二面角 的大小为
的大小为 . …………………12分
. …………………12分
 (解法二)设
(解法二)设 中点为
中点为 ,以
,以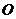 为坐标原点,
为坐标原点, 、
、 、
、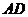 方向
方向
分别为 轴、
轴、 轴、
轴、 轴方向建立空间直角坐标系(如图)
轴方向建立空间直角坐标系(如图)
设
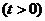 ,则点
,则点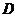 的坐标为
的坐标为
在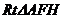 中,
中, ,
, ,
,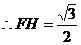 .
.
 点
点 的坐标为
的坐标为 ,点
,点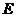 的坐标为
的坐标为 ,
,
 ,
,
设平面 的法向量为
的法向量为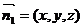 ,则
,则 ,
, .
.
即 令
令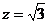 ,解得
,解得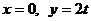
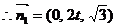 …………………10分
…………………10分
取平面 的一个法向量为
的一个法向量为 ,依题意
,依题意 与
与 的夹角为
的夹角为
 ,即
,即 ,
解得
,
解得 (负值舍去)
(负值舍去)
因此,当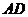 的长为
的长为 时,二面角
时,二面角 的大小为
的大小为 . …………………12分
. …………………12分
4、(2009番禺一模)如图,在四棱锥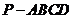 中,底面
中,底面 是边长为
是边长为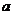 的正方形,侧面
的正方形,侧面
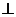 底面
底面 ,
,
 且
且 ,若
,若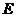 、
、 分别为线段
分别为线段 、
、 的中点.
的中点.
(1) 求证:直线 // 平面
// 平面 ;
;
(2) 求证:平面 平面
平面 ;
;
(3) 求二面角 的正切值.
的正切值.
(1)证明:连结 ,在
,在 中
中 //
// ……2分
……2分
且
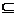 平面
平面 ,
, 平面
平面

 ……………………………………………………….4分
……………………………………………………….4分
(2)证明:因为面
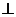 面
面 平面
平面
 面
面


所以, 平面
平面
 …………………………………………6分
…………………………………………6分
又 ,所以
,所以 是等腰直角三角形,且
是等腰直角三角形,且
即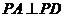 ……………………………………………………………….8分
……………………………………………………………….8分
 ,且
,且 、
、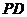
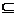 面
面

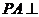 面
面
 又
又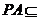 面
面 面
面 面
面 ………………………………………………………10分
………………………………………………………10分
(3)解:设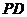 的中点为
的中点为 ,连结
,连结 ,
, ,则
,则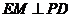
由(Ⅱ)知 面
面 ,
, 
 面
面

 是二面角
是二面角 的平面角………………………12分
的平面角………………………12分
 中,
中,

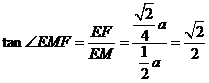 故所求二面角的正切为
故所求二面角的正切为 ……14分
……14分
 另解:如图,取
另解:如图,取 的中点
的中点 , 连结
, 连结 ,
, .
.
∵ , ∴
, ∴ .
.
∵侧面
 底面
底面 ,
, ,
,
∴ ,
,
而 分别为
分别为 的中点,∴
的中点,∴ ,又
,又 是正方形,故
是正方形,故 .
.
∵ ,∴
,∴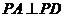 ,
, .
.
以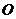 为原点,直线
为原点,直线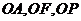 为
为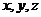 轴建立空间直线坐标系,则有
轴建立空间直线坐标系,则有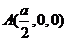 ,
, ,
,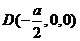 ,
, ,
,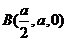 ,
, .
.
∵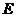 为
为 的中点, ∴
的中点, ∴ .
.
(1)易知平面 的法向量为
的法向量为 而
而 ,
,
且 , ∴
, ∴ //平面
//平面 .
.
(2)∵ ,
, ∴
∴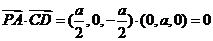 ,
,
∴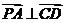 ,从而
,从而 ,又
,又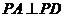 ,
, ,
,
∴ ,而
,而 , ∴平面
, ∴平面 平面
平面
(3)由(2)知平面 的法向量为
的法向量为 .
.
设平面 的法向量为
的法向量为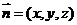 .∵
.∵ ,
,
∴由 可得
可得 ,令
,令 ,则
,则 ,
,
故 ,∴
,∴ ,
,
即二面角 的余弦值为
的余弦值为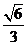 ,二面角
,二面角 的正切值为
的正切值为 .
.
3.(2009广东三校一模)如图,在梯形 中,
中,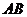 ∥
∥ ,
, ,
,

 ,平面
,平面 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,点
,点 在线段
在线段 上.
上.
(1)求证: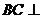 平面
平面 ;
;
(2)当 为何值时,
为何值时, ∥平面
∥平面 ?证明你的结论;
?证明你的结论;
(3)求二面角 的平面角的余弦值.
的平面角的余弦值.
(Ⅰ)在梯形 中,
中,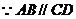 ,
,


 四边形
四边形 是等腰梯形,
是等腰梯形,
且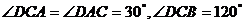

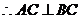 2分
2分
又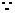 平面
平面 平面
平面 ,交线为
,交线为 ,
,
 平面
平面 4分
4分
(Ⅱ)解法一、当 时,
时, 平面
平面 ,
5分
,
5分
在梯形 中,设
中,设 ,连接
,连接 ,则
,则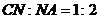 6分
6分
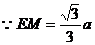 ,而
,而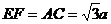
 ,
7分
,
7分
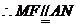 ,
, 四边形
四边形 是平行四边形,
是平行四边形, 8分
8分
又 平面
平面 ,
, 平面
平面
 平面
平面 9分
9分
解法二:当 时,
时, 平面
平面 ,
,
由(Ⅰ)知,以点 为原点,
为原点, 所在直线为坐标轴,建立空间直角坐标系,
所在直线为坐标轴,建立空间直角坐标系,
5分
 则
则 ,
, ,
, ,
, ,
,
 ,
,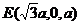
 平面
平面 ,
,

 平面
平面

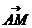 与
与 、
、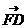 共面,
共面,
也等价于存在实数 、
、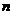 ,使
,使 ,
,
设 .
.
 ,
,

又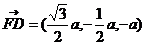 ,
,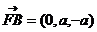 ,
6分
,
6分
从而要使得: 成立,
成立,
需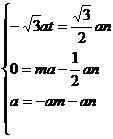 ,解得
,解得 8分
8分
 当
当 时,
时, 平面
平面 9分
9分
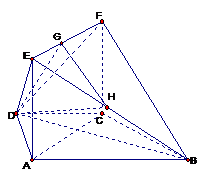 (Ⅲ)解法一、取
(Ⅲ)解法一、取 中点
中点 ,
, 中点
中点 ,连结
,连结 ,
,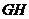 ,
,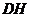

 平面
平面

又 ,
, ,又
,又 ,
,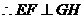

 是二面角
是二面角 的平面角.
6分
的平面角.
6分
在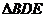 中,
中,
 ,
, .
7分
.
7分
又 .
8分
.
8分
 在
在 中,由余弦定理得
中,由余弦定理得 ,
9分
,
9分
即二面角 的平面角的余弦值为
的平面角的余弦值为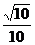 .
.
 解法二:由(Ⅰ)知,以点
解法二:由(Ⅰ)知,以点 为原点,
为原点, 所在直线为坐标轴,
所在直线为坐标轴,
建立空间直角坐标系,则 ,
, ,
, ,
,
 ,
, ,
,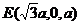 过
过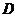 作
作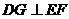 ,
,
垂足为 . 令
. 令 ,
,
 ,
, 
由 得,
得, ,
,
 ,即
,即 11分
11分
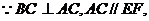
 ,
,
 二面角
二面角 的大小就是向量
的大小就是向量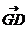 与向量
与向量 所夹的角.
12分
所夹的角.
12分
 13分
13分

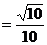
即二面角 的平面角的余弦值为
的平面角的余弦值为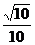 .
14分
.
14分
2.如图,已知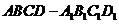 是棱长为
是棱长为 的正方体,点
的正方体,点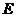 在
在 上,点
上,点 在
在 上,且
上,且 .
.
 (1)求证:
(1)求证: 四点共面;(4分);(2)若点
四点共面;(4分);(2)若点 在
在 上,
上, ,点
,点 在
在 上,
上, ,垂足为
,垂足为 ,求证:
,求证: 平面
平面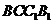 ;(4分);(3)用
;(4分);(3)用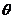 表示截面
表示截面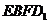 和侧面
和侧面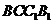 所成的锐二面角的大小,求
所成的锐二面角的大小,求 .
.
证明:(1)建立如图所示的坐标系,则 ,
, ,
, ,
,
所以 ,故
,故 ,
, ,
,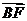 共面.又它们有公共点
共面.又它们有公共点 ,所以
,所以 四点共面.
四点共面.
(2)如图,设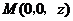 ,则
,则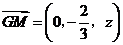 ,而
,而 ,由题设得
,由题设得 ,
,
得 .因为
.因为 ,
, ,有
,有 ,又
,又 ,
, ,所以
,所以 ,
, ,从而
,从而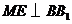 ,
, .故
.故 平面
平面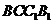 .
.
(3)设向量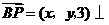 截面
截面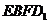 ,于是
,于是 ,
,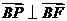 .
.
而 ,
, ,得
,得 ,
, ,解得
,解得 ,
, ,所以
,所以 .又
.又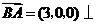 平面
平面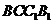 ,所以
,所以 和
和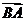 的夹角等于
的夹角等于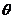 或
或 (
(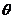 为锐角).
为锐角).
于是 . 故
. 故 .
.
1.如图,在三棱锥 中,
中, ,
,

 ,
,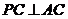 .
.
(Ⅰ)求证: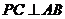 ;(Ⅱ)求二面角
;(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
解法一:(Ⅰ)取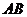 中点
中点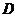 ,连结
,连结 .
.
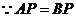 ,
, .
.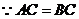 ,
,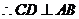 .
.

 ,
, 平面
平面 .
.
 平面
平面 ,
, .
.
(Ⅱ)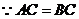 ,
,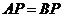 ,
,
 .又
.又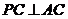 ,
, .
.
又 ,即
,即 ,且
,且 ,
,
 平面
平面 .取
.取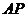 中点
中点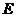 .连结
.连结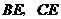 .
.
 ,
, .
. 是
是 在平面
在平面 内的射影,
内的射影,
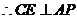 .
.
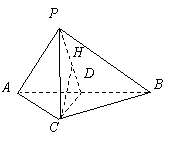
 是二面角
是二面角 的平面角.在
的平面角.在 中,
中,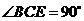 ,
, ,
, ,
, .
.
 二面角
二面角 的大小为
的大小为 .
.
(Ⅲ)由(Ⅰ)知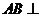 平面
平面 ,
, 平面
平面 平面
平面 .过
.过 作
作 ,垂足为
,垂足为 .
.
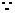 平面
平面 平面
平面 ,
, 平面
平面 .
. 的长即为点
的长即为点 到平面
到平面 的距离.
的距离.
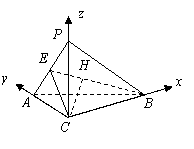 由(Ⅰ)知
由(Ⅰ)知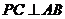 ,又
,又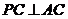 ,且
,且 ,
, 平面
平面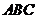 .
.
 平面
平面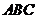 ,
, .
.
在 中,
中,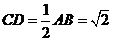 ,
, ,
,
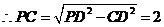 .
. .
.
 点
点 到平面
到平面 的距离为
的距离为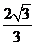 .
.
解法二:(Ⅰ)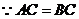 ,
,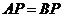 ,
, .又
.又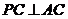 ,
, .
.
 ,
, 平面
平面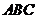 .
. 平面
平面 ,
, .
.
(Ⅱ)如图,以 为原点建立空间直角坐标系
为原点建立空间直角坐标系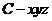 .则
.则 .
.
设 .
.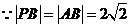 ,
, ,
,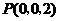 .取
.取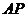 中点
中点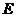 ,连结
,连结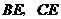 .
.
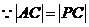 ,
, ,
,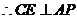 ,
, .
. 是二面角
是二面角 的平面角.
的平面角.
 ,
, ,
, ,
,
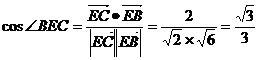 .
. 二面角
二面角 的大小为
的大小为 .
.
(Ⅲ) ,
, 在平面
在平面 内的射影为正
内的射影为正 的中心
的中心 ,且
,且 的长为点
的长为点 到平面
到平面 的距离.
的距离.
如(Ⅱ)建立空间直角坐标系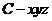 .
.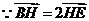 ,
, 点
点 的坐标为
的坐标为 .
.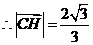 .
.
 点
点 到平面
到平面 的距离为
的距离为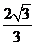 .
.
4.等边三角形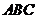 与正方形
与正方形 有一公共边
有一公共边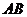 ,二面角
,二面角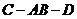 的余弦值为
的余弦值为 ,
, 分别是
分别是 的中点,则
的中点,则 所成角的余弦值等于
所成角的余弦值等于
 答案
答案  .
.
3.某几何体的一条棱长为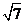 ,在该几何体的正视图中,这条棱的投影是长为
,在该几何体的正视图中,这条棱的投影是长为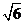 的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )A.
的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )A. B.
B.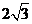 C.
C. D.
D.
答案 C
2. (2009昆明一中第三次模拟)如图,正四棱柱
(2009昆明一中第三次模拟)如图,正四棱柱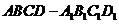 中,
中, ,则异面直线
,则异面直线 与
与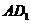 所成角的余弦值为( )
所成角的余弦值为( )
A. B.
B.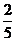
C. D.
D.
答案 D
1. 连结球面上两点的线段称为球的弦.半径为4的球的两条弦AB、CD的长度分别等于2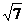 、4
、4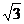 ,M、N分别为AB、CD的中点,每条弦的两端都在球面上运动,有下列四个命题:
,M、N分别为AB、CD的中点,每条弦的两端都在球面上运动,有下列四个命题:
①弦AB、CD可能相交于点M ②弦AB、CD可能相交于点N ③MN的最大值为5 ④MN的最小值为l,其中真命题的个数为
A.1个 B.2个 C.3个 D.4个
答案 C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com