
题目列表(包括答案和解析)
14.(天津和平区2009高三一模)在△ABC中, ,
,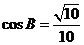 .
.
(Ⅰ)求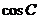 ;
;
(Ⅱ)设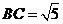 ,求
,求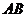 .
.
解 (Ⅰ)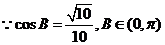
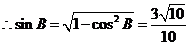
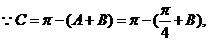
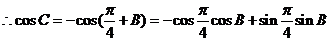
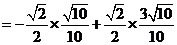
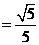
(Ⅱ)
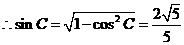 .
.
由已知条件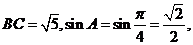
根据正弦定理,得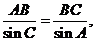
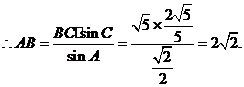
13.(山东省潍坊市2009高三一模)△ABC中,a,b,c分别是角A,B,C的对边,向量m=(2sinB,2-cos2B),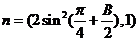 ,m⊥n,
,m⊥n,
(1)求角B的大小;
(2)若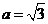 ,b=1,求c的值.
,b=1,求c的值.
解:(I)  ,………2分
,………2分
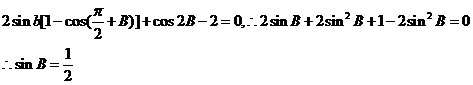
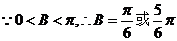
(Ⅱ) 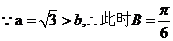
方法一:由余弦定理得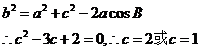
方法二:由正弦定理得
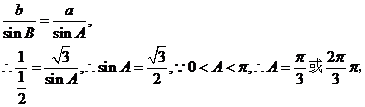
若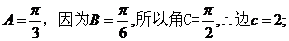
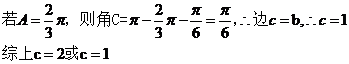
12.(山东省试验中学2009年高三第三次诊断性考试)在 中,
中,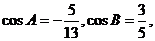
(1)求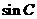 的值
的值
(2)设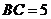 ,求
,求 的面积
的面积
.解(I)由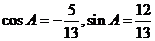 ,得
,得
由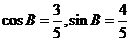 ,得
,得
又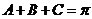
所以
(II)由正弦定理得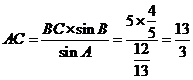
所以 的面积
的面积
11.(山东省济宁市2009高三第一阶段质量检测)在 中,
中,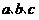 分别为角
分别为角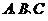 的对边,且满足
的对边,且满足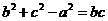 .
.
(Ⅰ)求角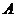 的值;
的值;
(Ⅱ)若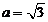 ,设角
,设角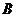 的大小为
的大小为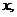
 的周长为
的周长为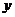 ,求
,求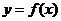 的最大值.
的最大值.
解:(Ⅰ)在 中,由
中,由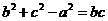 及余弦定理得
及余弦定理得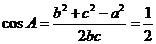
而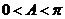 ,则
,则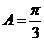 ;
;
(Ⅱ)由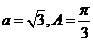 及正弦定理得
及正弦定理得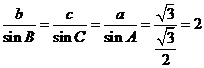 ,
,
而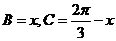 ,则
,则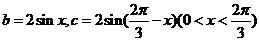
于是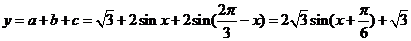 ,
,
由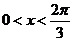 得
得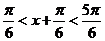 ,当
,当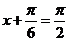 即
即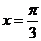 时,
时,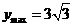
10.(新宾高中2009届高三年级第一次模拟考试)在△ABC中,tanA= ,tanB=
,tanB=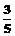 .
.
(1)求角C的大小;
(2)若AB边的长为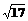 ,求BC边的长.
,求BC边的长.
解 (Ⅰ)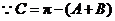 ,
,
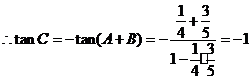 .又
.又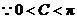 ,
,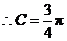 .(6分)
.(6分)
(Ⅱ)由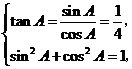 且
且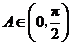 ,
,
得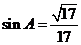 .
.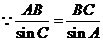 ,
,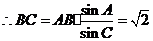 .(6分)
.(6分)
9.(辽宁省抚顺市2009模拟)在 中,
中,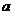 、
、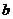 、
、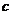 分别是角
分别是角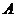 、
、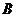 、
、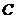 的对边,且
的对边,且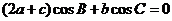 .
.
(Ⅰ)求角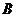 的值;
的值;
(Ⅱ)若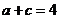 ,求
,求 面积
面积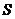 的最大值.
的最大值.
解
(Ⅰ)由正弦定理得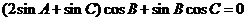 ,
,
即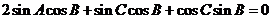
得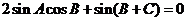 ,因为
,因为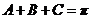 ,所以
,所以 ,得
,得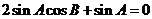 ,因为
,因为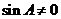 ,
,
所以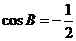 ,又
,又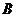 为三角形的内角,所以
为三角形的内角,所以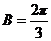
(Ⅱ) ,由
,由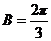 及
及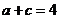 得
得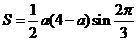
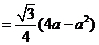
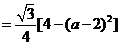 ,
,
又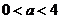 ,所以当
,所以当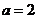 时,
时,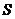 取最大值
取最大值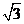 ……3分
……3分
8.(广东省广州市2009年模拟)已知△ABC的内角A、B、C所对的边分别为a,b,c,且a=2, cosB=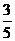 .
.
(1)若b=4,求sinA的值; (2) 若△ABC的面积S△ABC=4,求b,c的值.
解:(1) ∵cosB=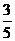 >0,且0<B<π,
>0,且0<B<π,
∴sinB=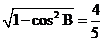 .
.
由正弦定理得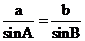 ,
,
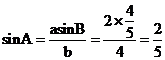 .
.
(2) ∵S△ABC=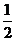 acsinB=4,
acsinB=4,
∴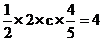 , ∴c=5.
, ∴c=5.
由余弦定理得b2=a2+c2-2accosB,
∴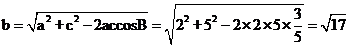 .
.
7.(2009东北育才、天津耀华、大连育明、哈三中联考)在锐角 中,已知内角
中,已知内角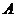 、
、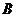 、
、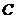 所对的边分别为
所对的边分别为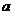 、
、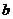 、
、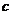 ,向量
,向量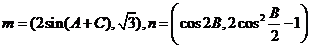 ,且向量
,且向量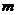 ,
,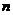 共线。
共线。
(1)求角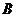 的大小;
的大小;
(Ⅱ)如果 ,求
,求 的面积
的面积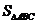 的最大值。
的最大值。
解:(1)由向量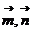 共线有:
共线有:
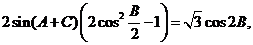
即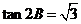 ,
2分
,
2分
又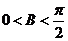 ,所以
,所以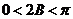 ,
,
则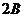 =
=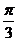 ,即
,即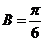 4分
4分
(Ⅱ)由余弦定理得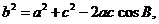 则
则
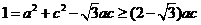 ,
,
所以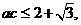 当且仅当
当且仅当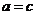 时等号成立 9分
时等号成立 9分
所以 。
10分
。
10分
6.(辽宁省沈阳二中2008-2009学年上学期高三期中考试) 在△ABC中,设A、B、C的对
边分别为a、b、c向量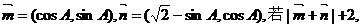
(1)求角A的大小;
(2)若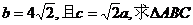 的面积.
的面积.
解(1)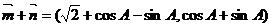
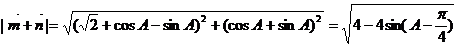
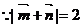
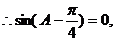
又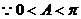
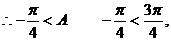
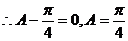
(2)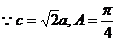
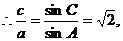
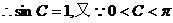
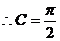
 为等腰三角形,
为等腰三角形,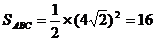
5.(2009宜春)已知向量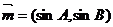 ,
,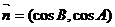 ,
,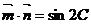 ,且
,且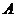 、
、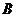 、
、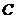 分别为
分别为 的三边
的三边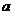 、
、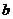 、
、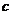 所对的角。
所对的角。
(1) 求角C的大小;
(2)
若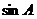 ,
,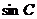 ,
,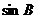 成等差数列,且
成等差数列,且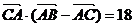 ,求
,求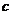 边的长。
边的长。
解:(1)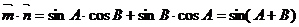
对于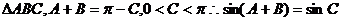 ,
,
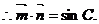
又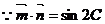 ,
,
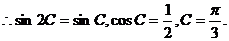
(2)由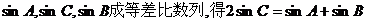 ,
,
由正弦定理得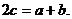
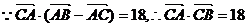 ,
,
即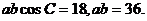
由余弦弦定理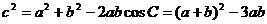 ,
,
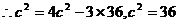 ,
,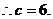
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com