14．如果学生甲每次投篮投中的概率为，那么他连续投三次，恰好两次投中的概率为__________；至少有一次投中的概率为__________(用数字作答)．

答案：　

解析：①C()²()＝，②“至少有一次投中”的对立事件是“一次都没投中”．“一次都没投中”的概率为＝()³＝，故“至少有一次投中”的概率为P＝1－＝1－＝.

总结评述：本题考查了对立事件的概率这个知识点．本题易错点：不会运用对立事件的概率，计算繁琐，导致耗时易错．

13．(2009·安徽普通高校模拟)一个口袋中装有大小相同的2个白球和3个黑球，从中摸出一个球，放回后再摸出一个球，则两次摸出的球恰好颜色不同的概率为________．

答案：

解析：P＝＝.

12．(2010·江西重点中学模拟)连掷两次骰子得到的点数分别为m和n，记向量a＝(m，n)与向量b＝(1，－1)的夹角为θ，则θ∈(0，]的概率是　　　　　　　　　　　　　　　　　　 (　)

A.　 B.　 C.　 D.

答案：C

解析：∵m＞0，n＞0，

∴a＝(m，n)与b＝(1，－1)不可能同向．

∴夹角θ≠0.

∵θ∈(0，]⇔a·b≥0，∴m－n≥0，

即m≥n.

当m＝6时，n＝6,5,4,3,2,1；

当m＝5时，n＝5,4,3,2,1；

当m＝4时，n＝4,3,2,1；

当m＝3时，n＝3,2,1；

当m＝2时，n＝2,1；

当m＝1时，n＝1.

∴概率是＝.故选C.

第Ⅱ卷(非选择题　共90分)

11．设两个独立事件A和B都不发生的概率为，A发生B不发生的概率与B发生A不发生的概率相同，则事件A发生的概率P(A)是　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A. 　　　　　　　　　　 　B. 　　　　　　　　　 　C. 　　　　　　 　D.

答案：D

解析：由题意，P()·P()＝，

P()P(B)＝P(A)P()，

设P(A)＝x，P(B)＝y，

则，即

∴x²－2x+1＝，

∴x－1＝－或x－1＝(舍去)，∴x＝.

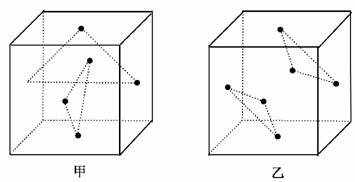
10．(2009·安徽，10)考察正方体6个面的中心，从中任意选3个点连成三角形，再把剩下的3个点也连成三角形，则所得的两个三角形全等的概率等于　　　　　　　　　　　　　　 (　)

A．1　 　　　　　 B. 　　　　　　　 　C.　　　　　　　　　　　　　　 　 D．0

答案：A

解析：正方体六个面的中心任取三个只能组成两种三角形，一种是等腰直角三角形，如图甲．另一种是正三角形如图乙．若任取三个点构成的是等腰直角三角形，剩下的三个点也一定构成等腰直角三角形，若任取三个点构成的是正三角形，剩下的三点也一定构成正三角形．这是一个必然事件，因此概率为1.

9．箱内有大小相同的6个红球和4个黑球，从中每次取1个球记下颜色后再放回箱中，则前3次恰有1次取到黑球的概率为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　 B.　　　　　　 　 C.　 　　　　　　　　　　 D.

答案：D

解析：每一次取到黑球的概率均为＝，则前3次恰有1次取到黑球的概率为C()·()²＝.故选D.

8．有一个篮球运动员投篮三次，三次投篮命中率均为，则这个篮球运动员投篮至少有一次投中的概率是　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．0.216 　　 　B．0.504　　 C．0.72 　　 　　　 D．0.936

答案：D

解析：至少有一次投中的概率为1－(1－)³＝0.936，故选D.

7．某校A班有学生40名，其中男生24人，B班有学生50名，其中女生30人，现从A、B两班各找一名学生进行问卷调查，则找出的学生是一男一女的概率为　　　　　　　 (　)

A.　　　　　　　　　　 　 B.　　　　　 　 C.　　　　　 　 D.

答案：B

解析：所找学生为A班男生B班女生的概率为×，为B班男生A班女生的概率为×.故所求概率为，选B.

6．为了庆祝六一儿童节，某食品厂制作了3种不同的精美卡片，每袋食品随机装入一张卡片，集齐3种卡片可获奖，现购买该食品5袋，能获奖的概率为　　　　　　　　　　 (　)

A. 　　　　　　 　B. 　　　　　 　C.　 　　　　 D.

答案：D

解析：本题考查的是古典概型，其中n＝3⁵，不能获奖的取法有C(2⁵－1)种，故获奖概率P＝1－＝，故选D.

5．(2009·江西，10)甲、乙、丙、丁4个足球队参加比赛，假设每场比赛各队取胜的概率相等，现任意将这4个队分成两个组(每组两个队)进行比赛，胜者再赛．则甲、乙相遇的概率为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　 B. 　　　　　　　 　C. 　　　　　　 　D.

答案：D

解析：甲、乙在同一组：P₁＝.

甲、乙不在同一组，但相遇的概率：P₂＝··＝，综上所述，甲、乙相遇的概率为P＝+＝.