
题目列表(包括答案和解析)
6.(2008·安徽理,7)a<0方程ax2+2x+1=0至少有一个负数根的 条件.
答案 充分不必要
5.在△ABC中,“sin2A=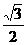 ”是“A=30°”的
条件.
”是“A=30°”的
条件.
答案 必要不充分
4.(2009·成化高级中学高三期中考试)已知函数f(x)=ax+b(0≤x≤1),则“a+2b>0” “是f(x)>0”恒成立的
条件.(填“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”之一)
答案 必要不充分
3.“x>1”是“x2>x”的 条件.
? 答案 充分不必要
2.(2008·重庆理,2)设m,n是整数,则“m,n均为偶数”是“m+n是偶数”的 条件.
答案 充分不必要
1.下列命题:①5>4或4>5;②9≥3;③命题“若a>b,则a+c>b+c”的否命题;④命题“矩形的两条对角线相等”的逆命题.其中假命题的个数为 .
答案 1
12.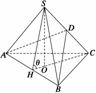 三棱锥S-ABC中,一条棱长为a,其余棱长均为1,求a为何值时
三棱锥S-ABC中,一条棱长为a,其余棱长均为1,求a为何值时
VS-ABC最大,并求最大值.
解 方法一 如图所示,设SC=a,其余棱长均为1,
取AB的中点H,连接HS、HC,则AB⊥HC,AB⊥HS,
∴AB⊥平面SHC.
在面SHC中,过S作SO⊥HC,则SO⊥平面ABC.
在△SAB中,SA=AB=BS=1,∴SH=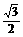 ,
,
设∠SHO=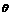 ,则SO=SHsin
,则SO=SHsin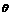 =
=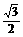 sin
sin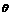 ,
,
∴VS-ABC=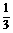 S△ABC·SO=
S△ABC·SO=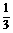 ×
×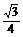 ×12×
×12×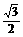 sin
sin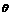 =
=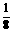 sin
sin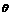 ≤
≤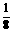 .
.
当且仅当sin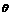 =1,即
=1,即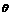 =90°时,三棱锥的体积最大.
=90°时,三棱锥的体积最大.
a=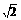 SH=
SH=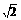 ×
×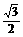 =
=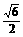 ,Vmax=
,Vmax=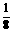 .∴a为
.∴a为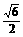 时,三棱锥的体积最大为
时,三棱锥的体积最大为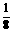 .
.
方法二 取SC的中点D,可通过VS-ABC=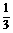 S△ABD·SC,转化为关于a的目标函数的最大值问题,利用基本不等式或配方法解决.
S△ABD·SC,转化为关于a的目标函数的最大值问题,利用基本不等式或配方法解决.
11.如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,
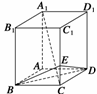 E是棱CC1上的点,且CE=
E是棱CC1上的点,且CE=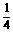 CC1.
CC1.
(1)求三棱锥C-BED的体积;
(2)求证:A1C⊥平面BDE.
(1)解 ∵CE=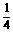 CC1=
CC1=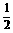 ,∴VC-BDE=VE-BCD=
,∴VC-BDE=VE-BCD=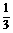 S△BCD·CE
S△BCD·CE
=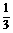 ×
×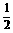 ×1×1×
×1×1×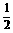 =
=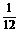 .
.
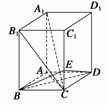 (2)证明 连接AC、B1C,∵AB=BC,∴BD⊥AC.
(2)证明 连接AC、B1C,∵AB=BC,∴BD⊥AC.
∵A1A⊥底面ABCD,∴BD⊥A1A.∵A1A∩AC=A,
∴BD⊥平面A1AC.∴BD⊥A1C.∵tan∠BB1C=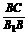 =
=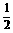 ,
,
tan∠CBE=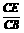 =
=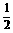 ,∴∠BB1C=∠CBE.∵∠BB1C+∠BCB1=90°,
,∴∠BB1C=∠CBE.∵∠BB1C+∠BCB1=90°,
∴∠CBE+∠BCB1=90°,∴BE⊥B1C.∵BE⊥A1B1,A1B1∩B1C=B1,
∴BE⊥平面A1B1C,∴BE⊥A1C.∵BD∩BE=B,BE 平面BDE,BD
平面BDE,BD 平面BDE,
平面BDE,
∴A1C⊥平面BDE.
10.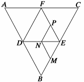 如图所示,正△ABC的边长为4,D、E、F分别为各边中点,M、N、P
如图所示,正△ABC的边长为4,D、E、F分别为各边中点,M、N、P
分别为BE、DE、EF的中点,将△ABC沿DE、EF、DF折成了三棱锥以后.
(1)∠MNP等于多少度?
(2)擦去线段EM、EN、EP后剩下的几何体是什么?其侧面积为多少?
解 (1)由题意,折成了三棱锥以后,如图所示,
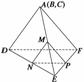 △MNP为正三角形,故∠MNP=∠DAF=60°.
△MNP为正三角形,故∠MNP=∠DAF=60°.
(2)擦去线段EM、EN、EP后,所得几何体为棱台,
其侧面积为S侧=SE-ADF侧-SE-MNP侧
=3×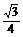 ×22-3×
×22-3×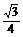 ×12=
×12=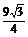 .
.
9.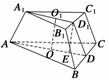 一个正三棱台的上、下底面边长分别是3 cm和6 cm,高是
一个正三棱台的上、下底面边长分别是3 cm和6 cm,高是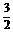 cm,
cm,
(1)求三棱台的斜高; (2)求三棱台的侧面积和表面积.
解 (1)设O1、O分别为正三棱台ABC-A1B1C1的上、下底面
正三角形的中心,如图所示,则O1O=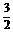 ,过O1作O1D1⊥B1C1,
,过O1作O1D1⊥B1C1,
OD⊥BC,则D1D为三棱台的斜高;过D1作D1E⊥AD于E,
则D1E=O1O=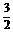 ,因O1D1=
,因O1D1=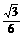 ×3=
×3=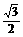 ,OD=
,OD=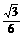 ×6=
×6=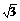 ,则DE=OD-O1D1=
,则DE=OD-O1D1=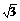 -
-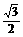 =
=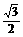 .
.
在Rt△D1DE中, D1D=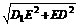 =
=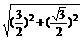 =
=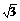 .
.
(2)设C、C′分别为上、下底的周长,h′为斜高,
S侧=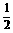 (C+C′)h′=
(C+C′)h′=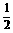 (3×3+3×6)×
(3×3+3×6)×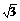 =
=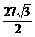 (cm2),
(cm2),
S表=S侧+S上+S下=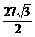 +
+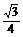 ×32+
×32+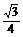 ×62=
×62=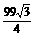 (cm2).
(cm2).
故三棱台斜高为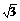 cm,侧面积为
cm,侧面积为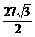 cm2,表面积为
cm2,表面积为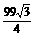 cm2.
cm2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com