
题目列表(包括答案和解析)
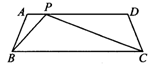
4.如图,在梯形ABCD中,AD∥BC,AD<BC,AD=5,AB=DC=2,P为AD上的一点,∠BPC=∠A.△ABP与△DPC相似吗?为什么?
[拓展与延伸]
3.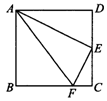 (1)P是Rt△ABC的斜边BC上异于点B、C的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( ).
(1)P是Rt△ABC的斜边BC上异于点B、C的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( ).
(A)1条 (B)2条 (C)3条 (D)4条
(2)如图,在正方形ABCD中,E是CD的中点,FC=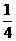 BC.图中与△ADE相似的三角形有( ).
BC.图中与△ADE相似的三角形有( ).
(A)0个 (B)1个 (C)2个 (D)3个
2.在△ABC中,点D、E分别在AB、AC上,AD=4,DB=2,AC=8.当AE=______时,△ADE∽△ABC;当AE=_______时,△ADE∽△ACB.
1.根据下列条件,试判别△A′B′C′与△ABC是否相似,并说明理由:
(1)∠A=70°,∠C=65°,∠A′=70°,∠B′=35°;
(2)∠B=55°,AB=6cm,BC=7cm,∠B′=55°,A′B′=18cm,B′C′=21cm;
(3)AB=10cm,BC=8cm,AC=16cm,A′B′=16cm,B′C′=12.8cm,A′C′=25.6cm.
2.通过对具体问题的分析和思考,提高分析问题和解决问题的能力.
[基础与巩固]
1.灵活运用三角形相似的不同条件解决问题,进一步体会判断三角形相似的各种方法的特征.
10.4 探索三角形相似的条件(4)同步练习
[目标与方法]
14.3求简单事件发生的可能性(二)
第1题. 某事件发生的概率为100%,则此事件( )
A.不可能发生 B.很有可能发生 C.必然发生 D.不太可能发生
答案:C.
第2题. 下列表示频率的数据,正确的是( )
A.1.3 B.-1.3 C.30 D.30%
答案:D.
第3题. 如果事件A发生的概率为99%,那么事件A( )
A.一定会发生 B.很可能会发生 C.可能不会发生 D.一定不发生
答案:B.
第4题. 一件事情发生的机会不可能是( )
A.110% B.100% C.50% D.0
答案:A.
第5题. 一个同学随手写下了一半数字:20022003200420052006,则0出现的频率是( )
A.10 B.20 C.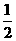 D.
D.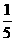
答案:C.
第6题. 一个袋子装有黄色球6个,白色球5个,红色球8个,蓝色球3个,每个球除了颜色外都相同,任意摸出一个球,摸到什么颜色的球的可能性较大?答:( ).
A.白色 B.红色 C.黄色 D.蓝色
答案:B.
第7题. 在一个不透明的口袋中,装有10个大小形状完全相同的小球,其中4个红球,3个黄球,2个白球,1个蓝球,摸到____颜色球的可能最大.
答案:红.
第8题. 在一个不透明的口袋中,装有10个大小形状完全相同的小球,其中4个红球,3个黄球,2个白球,1个蓝球,摸到白球的概率是______.
答案:20%.
第9题. 判断正误:如果一件事情不太可能发生,那么它就不可能发生.( )
答案:×.
第10题. 两直线平行,同旁内角相等,这个事件是_____发生的.
答案:可能.
第11题. 在英语句子"Are you a new student?"中,出现频数最大的字母是____,其频数是____,频率是______.
答案:e,3,0.176.
第12题. 在一副去掉大小王的扑克牌中,摸到一张大于10的牌的可能为______.
答案: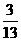 .
.
第13题. 若一件事情发生的机会是70%,则为____发生.
答案:可能.
第14题. 袋中装有4只红球,2只白球,1只黄球,这些球除了颜色以外完全相同,小明认为袋中只有三种不同颜色的球,所以从袋中任意摸出一只球,摸到红球,白球,黄球的可能性是一样大的,你认为呢?
答案:.不一样大,因为各自的个数不同.
第15题. “两个锐角的和大于180度”是____________的.(填 “必然发生”或“不可能发生”或“可能发生”)
答案:不可能.
第16题. “一个有理数的绝对值是负数”是____________的.(填 “必然发生”或“不可能发生”或“可能发生”)
答案:不可能.
第17题. 一副扑克牌(去掉大、小王),任意抽出一张牌,抽到一张花色为红色的牌的概率是多少?
答案:50%.

第18题. 如图是一个可自由转动的转盘,被均匀分成了相等的8个扇形,分别涂上黑红黄蓝色,求:转出红色的概率.
答案:25%.
第19题. 如图所示的转盘,判断下列事件发生的概率.
①指针指到数字4.
 ②指针指到数字1.
②指针指到数字1.
③指针指到的数字是一个偶数.
④指针指到的数字不是3.
⑤指针指到的数字小于6.
答案:①20%;②20%;③40%;④80%;⑤100%.
第20题. 有8个大小相同的球,设计一个摸球游戏,使摸到白球的概率为1/2,摸到红球的概率为1/4,摸到黄球的概率为1/4,摸到绿球的概率为0。则白球有____个,红球有____个,绿球有____个
答案:6,3,0.
第21题. 在题后横线上填上“必然发生”或“不可能发生”或“可能发生”掷两个普通的正方体骰子,把两个骰子的点数相加:
①和为1:____________;②和为6:____________;③和为12:____________.
答案:①不可能发生;②可能发生;③可能发生.
第22题. 有的同学会说:“既然我们不能在实验之前预知实验的确切结果,只知道每个结果的可能性,这对我们根本就没有意义.”这种说法对吗?能否举一个例子说明.
答案:说法不对.如甲、乙两厂生产同一产品,甲厂的次品率为0.001,乙厂的次品率为0.1,若两厂在其他方面条件相同,人们将愿意买甲厂的产品而不是乙厂的产品,尽管可能买到甲厂的次品,而买到乙厂的正品;又如“明天的降水概率为80%”,显然,带雨具比不带雨具要明智些,尽管明天不下雨.
第23题. 请设计一种均匀的正方体骰子,使他掷出后满足下列所有条件:(1)奇数点与偶数点朝上的概率相同;(2)大于2的点数与小于2的点数朝上的概率相同;(3)最大的数不超过4.
答案:答案不唯一,略.
第24题. 某校招收实验班学生,从每5个报名的学生中录取3人.如
果有100人报名,那么有 人可能被录取.
答案:60
第25题. 有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”,“08”,和“北京”的字块,如果婴儿能够排成“2008北京”或者“北京2008”,则他们就给婴儿奖励,假设该婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是
( )
A.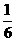 B.
B. 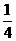 C.
C. 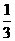 D.
D. 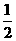
答案:C
第26题. 同时抛掷两枚均匀的硬币,则两枚硬币正面都向上的概率是
答案: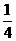 ;
;
第27题. 一个口袋中装有4个白球,2个红球,6个黄球,摇匀后随机
从中摸出一个球是白球的概率是 .
答案: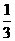
第28题. 一张圆桌旁有四个座位,A先坐在如图所示的座位上,B、C、D三人随机坐到其它三个座位上,求A与B不相邻而坐的概率.
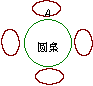
答案:解:由于 的位置已经确定,
的位置已经确定, 、
、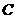 、
、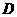 随机而坐的情况共有6种(如图):
随机而坐的情况共有6种(如图):
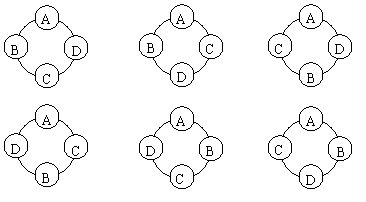
6种情况出现的可能性相同.其中 与
与 不相邻而坐的情况共有2种,所以所求概率是:
不相邻而坐的情况共有2种,所以所求概率是: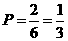 .
.
第29题. .小明的书包里装有外观完全相同的8本作业本,其中语文作业本3本,数学作业本3本,
英语作业本2本.小明从书包中随机抽出一本作业本是数学作业本的概率是 .
答案: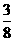
第30题. .一个袋中有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,都是蓝色珠子的概率是( )
(A)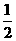 (B)
(B)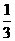 (C)
(C)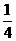 (D)
(D)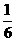
答案:D
14.3 求简单事件发生的可能性(三)同步试题
第1题. 必然事件发生的概率为_____;不可能事件发生的概率为____;不确定事件发生的概率在____和_____之间.
答案:1,0,0,1.
第2题. 一个盒子中有十个相同的白球,搅匀后从中任意摸一球,摸到白球的概率是( )
A.1 B.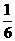 C.
C.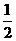 D.0
D.0
答案:A.
第3题. “山无凌,天地合”,这个事件是发生________的(填可能、不可能、必然)
答案:不可能.
第4题. 在一个袋子中装有50个黄色乒乓球,小明在里面随便摸出一个来,他摸到黄球的可能性是______,摸到白球的可能性是______.
答案:1,0.
第5题. 在口袋里放有3粒白色,2粒红色,1粒黑色的小球,它们只有颜色不同,任意摸出1粒,估计摸到红色小球的频率是_____.
答案: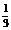
第6题. 正方体骰子,六个面上分别标有1,2,3,4,5,6.任意抛出,下面情况:①正面是3;②正面为合数;③正面为质数;④正面为6.机会相同的是( )
A.①② B.①③ C.①④ D.②③
答案:C
第7题. 两枚硬币,4个面中分别写上1、2、3、4,同时抛掷时,出现数字之积为奇数的机会( )
A.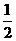 B.
B.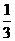 C.
C.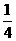 D
D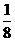
答案:C
第8题. 以下说法正确的是( )
A.在做剪刀、石头、布的游戏中,出现石头获胜机会最小
B.在做剪刀、石头、布的游戏中,三种获胜的机会都一样
C.由于抛掷硬币时出现正面朝上的机会是50%,则做10次,必有5次正面朝上
D.某彩标中奖率为1%,买100张必有一张中奖
答案:B
第9题. 一副完整的扑克牌,从中先摸一张是红桃A,第2张是方块8,第3张是黑桃9,第4张是小王,第5次摸到可能性最大的是( ).
A.老K B.梅花 C.5 D.方块
答案:C
第10题. 从一副 52 张(去掉大、小王)扑克牌中,任抽一张得到红桃的概率是( )
A.1 B.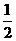 C.
C.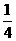 D.
D.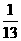
答案:C
第11题. 某科室10个人用抽签的方法分配两张观看"心连心"现场演出的票,第一个抽签的人得到票的概率是( )
A.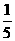 B.
B.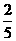 C.
C.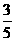 D.
D.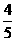
答案:A
第12题. 掷一棵骰子,得到2点的概率是( )
A.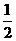 B.
B.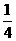 C.
C.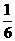 D.
D.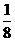
答案:C
第13题. 5个同学站成一排,其中某一人恰好站在中间的概率是( )
A.0 B.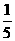 C.
C.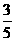 D.1
D.1
答案:B
第14题. 如图自由转动下面的转盘(转盘被等分成8个扇形),指针停在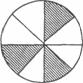 白色区域中的概率( )
白色区域中的概率( )
A.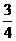 B.
B.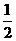 C.
C.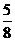 D.0
D.0
答案:C
第15题. 在口袋里放有3粒白色,2粒红色,1粒黑色的小球,它们只有颜色不同,任意摸出1粒,估计摸到红色小球的频率是_____.
答案: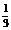
第16题. 把一副扑克中含有方块的13张牌洗匀后,任意抽出一张,
(1)P(抽到数字0)= ;
(2)P(抽到两位数)= ;
(3)P(抽到小于5)= .
答案:(1)0 (2)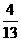 (3)
(3)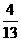
第17题. 必然事件的可能性是 ,不可能事件的可能性是 .
答案:1,0
第18题. 小刚自己做了一个骰子,两面是1,两面是2,另两面是3,任意投掷一次,掷得数是2的概率是 .
答案: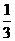
第19题. 一只老鼠在地上随意地跑,然后随意地走进图中所示的某个方格中(每个方格除颜色外完全一样),那么这只老鼠走进黑色方格中的概率是 .
答案: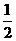
第20题. 从一副扑克牌(54张)中随便抽取一张牌,抽到大王的概率是 ,抽到方块9的概率是 ,抽到数字是6的概率是 .
答案: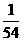 ,
,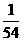 ,
,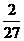
第21题. 下列事件中,发生的概率为1 的是( )
A.三天后会有大风降温 B.何明数学成绩为78分
C.今天是5号,明天是6号 D.2003年有368天
答案:C
第22题. 必然事件发生的概率为_____;不可能事件发生的概率为____;不确定事件发生的概率在____和_____之间.
答案:1,0,0,1
第23题. 从1到10这10个整数中任取一数,取到奇数的概率是 ,取得偶数的概率是 .
答案: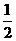 ,
,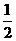
第24题. 把一枚骰子掷一次,得到点数小于2的概率是 ,得到点数是3的倍数的概率是 .
答案: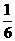 ,
,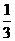
第25题. 掷一枚均匀的硬币,国徽朝上的概率是 .
答案: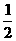
第26题. 掷一枚均匀的硬币,正面朝上的概率是______.
答案: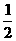 .
.
第27题. 1万张彩票中(1万张为一组),有一个特等奖,每组彩票全部售出后抽奖,已经卖出去9000张彩票,此时有个彩民购买了余下的全部彩票,则它中奖的概率为( )
A.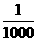 B.1 C.
B.1 C.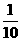 D.
D.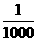
答案:C.
第28题. 设计一个有红、黄、绿三种颜色的转盘,使得指针转到红颜色的概率为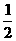 .至少写出三种设计方案.
.至少写出三种设计方案.
答案:略.
第29题. 下列是小马设计的四种转盘,三种颜色所占扇形面积的比例不同,当转动转盘,停止后,指针对向蓝色的可能性最大的是( )
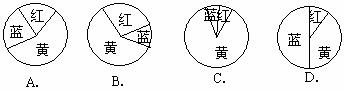
答案:D.
第30题.  如图所示,聪聪要通过转盘转出一个四位数,他转出第一个数字是6,则这四位数的最大值是______.转出这个数的概率是________.
如图所示,聪聪要通过转盘转出一个四位数,他转出第一个数字是6,则这四位数的最大值是______.转出这个数的概率是________.
答案:6999.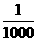 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com