
题目列表(包括答案和解析)
29、(1)解析式为: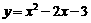 ………………………………………………2分
………………………………………………2分

(2)S四边形PQAC=-t2+ (1<t<3).……………………………………4分
(1<t<3).……………………………………4分
(3)假设存在这样的点N,使△NMC为等腰三角形.∵ 点N在BM上,不妨设N点坐标为(m,2m-6),则CM2=12+12=2,CN2=m2+[3-(6-2m)]2,或CN2=m2+[(6-2m)-3]2.
MN2=(m-1)2+[4-(6-2m)]2.△NMC为等腰三角形,有以下三种可能:
①若CN=CM,则m2+[(6-2m)-3]2=2,
∴ m1=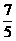 ,m2=1(舍去).∴ N(
,m2=1(舍去).∴ N(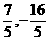 ).
).
②若MC=MN,则(m-1)2+[4-(6-2m)]2=12+12.∴ m=1±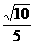 .∵ 1<m<3,
.∵ 1<m<3,
∴ m=1-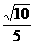 舍去.
舍去.
∴ N(1+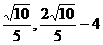 ).
).
③若NC=NM,则m2+[3-(6-2m)]2=(m-1)2+[4-(6-2m)]2.解得m=2.∴ N(2,-2).
综上所述,存在这样的点N,使△NMC为等腰三角形.且点N的坐标分别为: ,N3(2,-2).…………………………10分
,N3(2,-2).…………………………10分
28、(1)证△BEH≌△DEC……………………………………………………………5分
(2)证△BEH∽△GBA……………………………………………………………10分
27、解: 摸到红球、黄球、蓝球的概率分别是
摸到红球、黄球、蓝球的概率分别是
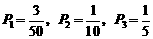 ……………………………………………………………3分
……………………………………………………………3分
又50×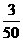 +30×
+30× +10×
+10×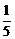 =8(元)(摸球所获购物券金额的平均数).…8分
=8(元)(摸球所获购物券金额的平均数).…8分
∵8元>5元,∴顾客选择摸奖方式是合算的.…………………………………10分
26、(1)①作图(略)…………………………………………………………………2分
②一次函数 …………………………………………………………………3分
③y=1.8x+32…………………………………………………………………4分
④将其余三对数值分别代入③中的式子,结果等式均成立 ∴ y与x的关系式成立 …………………………………………………………………6分
(2)当y=88时,88=1.8x+32 ∴ x≈31 ∴ 31-12=19℃
答:这一天台北的最高气温比沈阳约高19℃.……………………………8分
25、解:将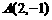 代入
代入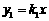 中,
中,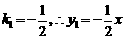 …………………………2分
…………………………2分
将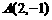 代入
代入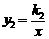 中,
中,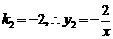 ……………………………4分
……………………………4分
由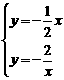 得,
得,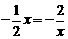
解得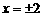 (舍去x=2)……………………………………………………7分
(舍去x=2)……………………………………………………7分
所以另一个交点为B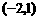 ……………………………………………………8分
……………………………………………………8分
24、(1)(每空1分,共4分)
|
|
平均数 |
方差 |
中位数 |
命中9环及以上次数 |
|
甲 |
|
|
7 |
1 |
|
乙 |
7 |
|
|
3 |
(2)测试结果分析(每小题1分,共4分)
①从平均数和方差来结合看,两者平均数相等,但甲的方差(1.2)小于乙的方差(5.4),所以甲的成绩更稳定;
②从平均数和中位数相结合看,两者平均数相等,但甲的中位数(7)小于乙的中位数(7.5),所以乙的成绩更好些;
③从平均数和命中9环及以上的次数相结合看,两者平均数相等,但甲命中9环及以上的次数(1次)小于乙命中9环及以上的次数(3次),所以乙的成绩更好些;
④从折线图上两人射击命中环数的走势看,乙命中环数的曲线整体呈上升趋势,所以乙更有潜力.
23、解:因为原方程有两个相等的实数根,所以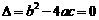
即 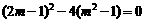 ,整理得
,整理得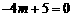 ,解得
,解得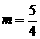 ………4分
………4分
原方程为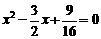 ,即
,即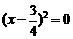
解得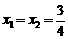 …………………………………………………………………8分
…………………………………………………………………8分
15、 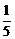 16、 4 17、
16、 4 17、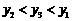 18、 ①③④
18、 ①③④
11、 < 12、 6 13、 m = 4 14、 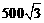
29.
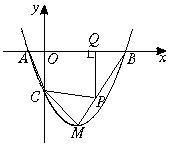 如图,抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当x=0和x=2时,y的值相等.直线y=3x - 7与这条抛物线相交于两点,其中一点的横坐标是4,另一点是这条抛物线的顶点M.
如图,抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当x=0和x=2时,y的值相等.直线y=3x - 7与这条抛物线相交于两点,其中一点的横坐标是4,另一点是这条抛物线的顶点M.
(1) 求这条抛物线的解析式;
(2) P为线段BM上一点,过点P向x轴引垂线,垂足为Q.若点P在线段BM上运动(点P不与点B、M重合),设OQ的长为t,四边形PQAC的面积为S.求S与t之间的函数关系式及自变量t的取值范围;
(3) 在线段BM上是否存在点N,使△NMC为等腰三角形?若存在,请求出点N的坐标;若不存在,请说明理由.
(命题人:夏 彬 审题人:李 伟)
西南师大附中2008-2009学年度下期期末考试
初二数学试题
(总分:150分 考试时间:120分钟)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com