
题目列表(包括答案和解析)
1.一次函数y=3x+12的图象如图1所示,由此可知,方程3x+12=0的解为 .

2.(19分)已知杉杉服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)的函数关系式,并求出自变量的取值范围.
(2)当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多少?
1.(18分)已知:直线x-2y=-k+6和x+3y=4k+1,若它们的交点在第四象限内.
(1)求k的取值范围.
(2)若k为非负整数,求直线x-2y=-k+6和x+3y=4k+1分别与y轴的交点,及它们的交点所围成的三角形的面积.
某单位急需用车,但又不准备买车,他们准备和一个体车主或一国营出租车公司其中的一家签订租车合同,设汽车每月行驶x(千米),应付给个体车主的费用是y1(元),应付给出租车公司的费用是y2(元),y1、y2分别与x之间的函数关系图象(两条射线)如图2,观察图象回答下列问题:
(1)每月行驶的路程在什么范围内,租国营公司的车合算?
(2)每月行驶的路程为多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300千米,那么这个单位租用哪家的车合算?

3.已知直线y=kx+b过点A(x1,y1),点B(x2,y2),若k<0时,x1<x2,则y1与y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
2.如图1所示,直线l1,l2的交点坐标可以看作是一个方程组的解,则这个方程组是( )
 A.
A.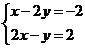 B.
B.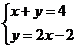
C.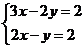 D.
D.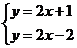
1.以方程x-y+2m=0和x+y=4的解为坐标的点P(x,y)一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.一次函数y=(3m-1)x-m中,y随x的增大而减小,且其图象不经过第一象限,则m的取值范围是 .
2.若直线y=3x-1与y=x-k的交点在第四象限,则k的取值范围是 .
1.一次函数y=2x+3与y=2x-3的图象的位置关系是
,即 交点(填“有”或“没有”),由此可知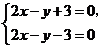 的解的情况是
.
的解的情况是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com