
题目列表(包括答案和解析)
4.已知直角三角形两直角边长的和为17,斜边长为13,则斜边上的高为 .
3.某种品牌的电脑,原价是7 200元/台,经过连续两次降价后,现价是3 528元/台,平均每次降价的百分率为 .
2.直角三角形两条直角边长的比是5∶12,斜边长为130cm,则这个直角三角形的面积是
cm2.
1.长方形的长比宽多3cm,面积为70cm2,长方形的周长为 cm.
11.勾股定理及其逆定理的应用
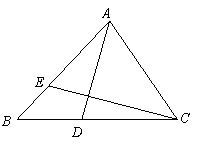
第1题. (2007安徽课改,10分)如图,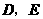 分别是
分别是 的边
的边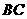 和
和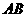 上的点,
上的点,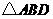 与
与 的周长相等,
的周长相等, 与
与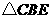 的周长相等.设
的周长相等.设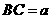 ,
,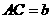 ,
,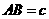 .
.
 (1)求
(1)求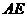 和
和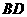 的长;
的长;
(2)若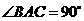 ,
, 的面积为
的面积为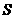 ,求证:
,求证: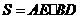 .
.
答案:解:(1)
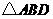 与
与 的周长相等,
的周长相等,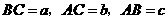 ,
,
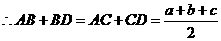 .
.
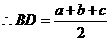
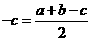 ;同理
;同理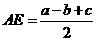 .
.
(2)
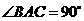 ,
,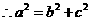 ,
,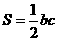 .
.
由(1)知 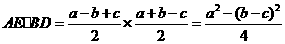
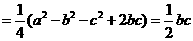 .
.
即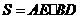 .
.
第2题. (2007安徽芜湖课改,4分)如图,所有的四边形都是正方形,所有的三角形都是直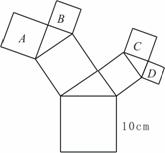 角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )
角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )
A. 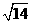 cm B.4cm C.
cm B.4cm C. 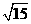 cm D. 3cm
cm D. 3cm
答案:A
第3题. 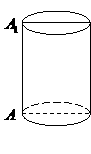 (2007广东梅州课改,3分)如图5,有一木质圆柱形笔筒的高为
(2007广东梅州课改,3分)如图5,有一木质圆柱形笔筒的高为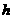 ,底面半径为
,底面半径为 ,现要围绕笔筒的表面由
,现要围绕笔筒的表面由 至
至 (
(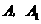 在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是
.
在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是
.
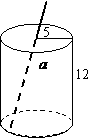 答案:
答案: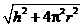
第4题. (2007广东茂名课改,4分)如图是一个圆柱形饮料罐,底面半径是5,高是12,上底 面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分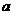 的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.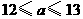 B.
B.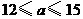
C.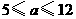 D.
D.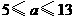
答案:A
第5题. (2007黑龙江佳木斯课改,6分)小强家有一块三角形菜地,量得两边长分别为40m,50m,第三边上的高为30m,请你帮小强计算这块菜地的面积(结果保留根号).
答案: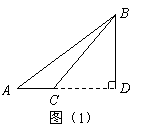 解:分两种情况:
解:分两种情况:
(1)如图(1)
当 为钝角时,
为钝角时,

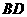 是高,
是高,
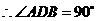 .
.
在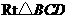 中,
中,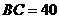 ,
,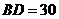

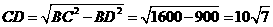 .
.
在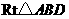 中,
中,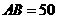 ,
,

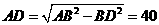 .
.
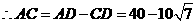 ,
,

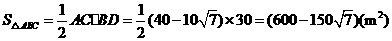 .
.
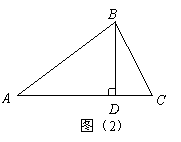 (2)如图(2)
(2)如图(2)
当 为锐角时,
为锐角时,

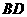 是高,
是高,
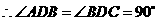 ,
,
在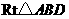 中,
中,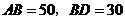 ,
,
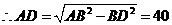 .
.
同理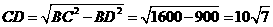 ,
,

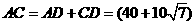 ,
,

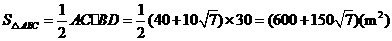 .
.
综上所述: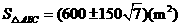
第6题. (2007湖北荆门课改,3分)我国古代数学家赵爽的“勾股圆方图”是由四个全 等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为
等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为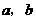 ,那么
,那么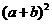 的值是 .
的值是 .
答案:25
第7题.  (2007湖南怀化课改,2分)如图所示的圆柱体中底面圆的半径是
(2007湖南怀化课改,2分)如图所示的圆柱体中底面圆的半径是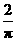 ,高为
,高为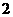 ,若一只小虫从
,若一只小虫从 点出发沿着圆柱体的侧面爬行到
点出发沿着圆柱体的侧面爬行到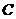 点,则小虫爬行的最短路程是 (结果保留根号)
点,则小虫爬行的最短路程是 (结果保留根号)
答案: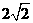
第8题. (2007江苏连云港课改,3分)如图,直线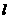 上有三个正方形
上有三个正方形 ,若
,若 的面积分别为5和
的面积分别为5和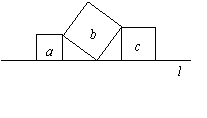 11,则
11,则 的面积为( )
的面积为( )
A.4 B.6 C.16 D.55
答案:C
第9题. (2007江苏徐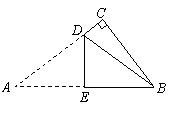 州课改,3分)如图,已知
州课改,3分)如图,已知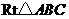 中,
中,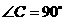 ,
,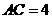 cm,
cm,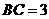 cm.现将
cm.现将 进行折叠,使顶点
进行折叠,使顶点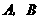 重合,则折痕
重合,则折痕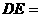 cm.
cm.
答案: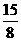
第10题. (2007江苏扬州课改,4分)如图是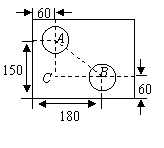 一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:
一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位: ),计算两圆孔中心
),计算两圆孔中心 和
和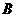 的距离为______
的距离为______ .
.
答案:150
第11题. (2007内蒙赤峰课改,4分)如图,在三角形纸片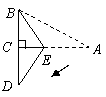
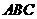 中,
中,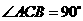 ,
,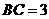 ,
,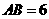 ,在
,在 上取一点
上取一点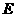 ,以
,以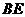 为折痕,使
为折痕,使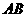 的一部分与
的一部分与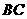 重合,
重合, 与
与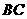 延长线上的点
延长线上的点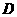 重合,则
重合,则 的长度为( )
的长度为( )
A.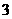 B.
B.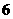 C.
C.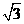 D.
D.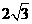
答案:C
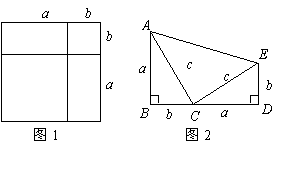
第12题. (2007山东聊城课改,10分)(1)如图1是一个重要公式的几何解释.请你写出这个公式;
(2)如图2,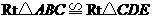 ,
,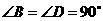 ,且
,且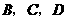 三点共线.
三点共线.
 试证明
试证明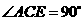 ;
;
(3)伽菲尔德( ,1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.
,1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.
答案:解:(1)这个公式为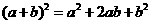 .
.
(2)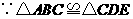 ,
,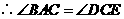 .
.
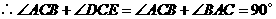 .
.
由于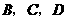 共线,
共线,
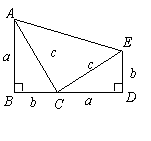
所以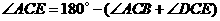
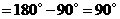 .
.
(3)梯形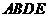 的面积为
的面积为
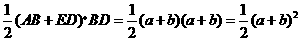 ;
;
另一方面,梯形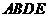 可分成三个直角三角形,其面积又可以表示成
可分成三个直角三角形,其面积又可以表示成
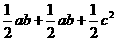 .
.
所以,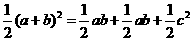 .
.
即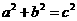 . 10分
. 10分
第13题. (2007山东威海课改,9分)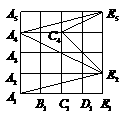 如图,正方形网格的每一个小正方形的边长都是1,试求
如图,正方形网格的每一个小正方形的边长都是1,试求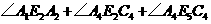 的度数.
的度数.
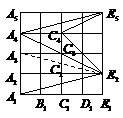 答案:解:连结
答案:解:连结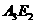 .
.
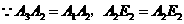 ,
,
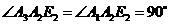 ,
,
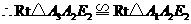 (SAS).
(SAS).
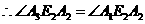 .
.
由勾股定理,得
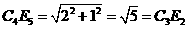 ,
,
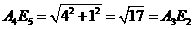 ,
,
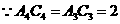 ,
,
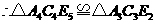 (SSS).
(SSS).
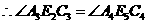 .
.
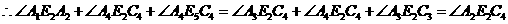 .
.
由图可知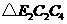 为等腰直角三角形.
为等腰直角三角形.
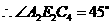 .
.
即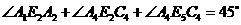 .
.
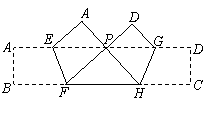
第14题. (2007四川乐山课改,3分)如图(5),把矩形纸条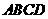 沿
沿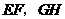 同时折叠,
同时折叠,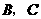 两点恰好落在
两点恰好落在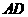 边的
边的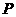 点处,若
点处,若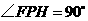 ,
,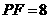 ,
,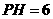 ,则矩形
,则矩形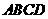 的边
的边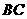 长为( )
长为( )
 A.
A.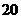 B.
B.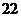 C.
C.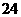 D.
D.
答案:C
第15题. (2007四川绵阳课改,4分)若a、b、c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
① 以a2,b2,c2 的长为边的三条线段能组成一个三角形
② 以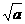 ,
,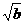 ,
,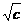 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形
③ 以a + b,c + h,h 的长为边的三条线段能组成直角三角形
④ 以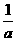 ,
,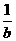 ,
,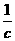 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形
其中所有正确结论的序号为 .
答案:②③④
第16题.  (2007湖南衡阳课改,3分)如图,
(2007湖南衡阳课改,3分)如图,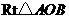 的斜边
的斜边 在
在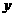 轴上,且
轴上,且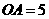 ,
,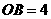 .将
.将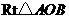 绕原点
绕原点 逆时针旋转一定的角度,使直角边
逆时针旋转一定的角度,使直角边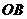 落在
落在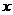 轴的负半轴上得到相应的
轴的负半轴上得到相应的 ,则
,则 点的坐标是 .
点的坐标是 .
答案: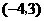
13.11-13.12勾股定理及其逆定理考题汇编
11.能够成为直角三角形三边长的三个正整数,我们称之为一组勾股数,观察下列表格所给出的三个数a,b,c,a<b<c.
(1)试找出它们的共同点,并证明你的结论.
(2)写出当a=17时,b,c的值.
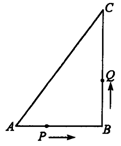
10.如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,问过3秒时,△BPQ的面积为多少?
◆拓展创新
|
3,4,5 |
32+42=52 |
|
5,12,13 |
52+122=132 |
|
7,24,25 |
72+242=252 |
|
9,40,41 |
92+402=412 |
|
… |
… |
|
17,b,c |
172+b2=c2 |
9.写出下列命题的逆命题,并判断真假.
(1)如果a=0,那么ab=0;
(2)如果x=4,那么x2=16;
(3)面积相等的三角形是全等三角形;
(4)如果三角形有一个内角是钝角,则其余两个角是锐角;
(5)在一个三角形中,等角对等边.
8.如图所示,四边形ABCD中,BA⊥DA,AB=2,AD=2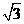 ,CD=3,BC=5,求∠ADC的度数.
,CD=3,BC=5,求∠ADC的度数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com